В самой природе человека заложено стремление к познанию мира, которое находит свое выражение в изучении и развитии особых отраслей знания – наук. Каждая наука, обращая свой взгляд на явления реального мира, вырабатывает специфические особенности, отличающие одну науку от другой. Суть любой науки заключается в объекте и предмете познания, причем разные науки могут иметь один объект познания, но разные предметы.

Объект науки– явления реального мира, на которые наука распространяет свое познание. Предмет науки – определенный круг вопросов относительно объекта исследования, которые относятся к части явления или к некоторым областям объекта. При выяснении предмета науки решается вопрос о том, что изучает данная наука. Принципы и методы изучения предмета науки составляют ее методологию.

Статистика – самостоятельная общественная наука, имеющая свой предмет и методы исследования, которая возникла из потребностей общественной жизни. Термин «статистика» происходит от латинского слова «статус», которое означает «положение, порядок». Впервые его употребил немецкий ученый Г. Ахенваль (1719–1772).

В настоящее время термин «статистика» употребляется в трех значениях:

• особая отрасль практической деятельности людей, направленная на сбор, обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отдельных отраслей экономики или предприятий;

• наука, занимающаяся разработкой теоретических положений и методов, используемых в статистической практике;

• статистические данные, представленные в отчетности предприятий, отраслей экономики, а также данные, публикуемые в сборниках, различных справочниках, бюллетенях и т. п.

Объект статистики – это явления и процессы социально-экономической жизни общества, в которых отражаются и находят свое выражение социально-экономические отношения людей. В зависимости от объекта изучения статистика как наука подразделяется на несколько блоков (рис. 1).

Отраслевые статистики

Рис. 1.1. Структура статистической науки

Общая теория статистики является методологической основой, ядром всех отраслевых статистик, она разрабатывает общие принципы и методы статистического исследования общественных явлений и является наиболее общей категорией статистики.

Задача экономической статистики – разработка и анализ синтетических показателей, отражающих состояние национальной экономики, взаимосвязи отраслей, особенности размещения производительных сил, наличие материальных, трудовых и финансовых ресурсов. Социальная статистика формирует систему показателей для характеристики образа жизни населения и различных аспектов социальных отношений.

В целом статистика занимается сбором информации различного характера, ее упорядочиванием, сопоставлением, анализом и интерпретацией (объяснением) и обладает следующими отличительными особенностями. Во-первых, статистика изучает количественную сторону общественных явлений: величину, размер, объем и имеет числовое значение. Во-вторых, статистика исследует качественную сторону явлений: специфику, внутреннюю особенность, отличающую одно явление от других. Качественная и количественная стороны явления всегда существуют вместе, образуя единство.

Все общественные явления и события протекают во времени и в пространстве, и в отношении любого из них всегда можно установить, когда оно возникло и где оно развивается. Таким образом, статистика изучает явления в конкретных условиях места и времени.

Изучаемые статистикой явления и процессы общественной жизни находятся в постоянном изменении, развитии. На основе сбора, обработки и анализа массовых данных об изменении изучаемых явлений и процессов выявляется статистическая закономерность. В статистических закономерностях проявляются действия общественных законов, которые определяют существование и развитие социально-экономических отношений в обществе.

Предметом статистики является изучение общественных явлений, динамики и направления их развития. При помощи статистических показателей данная наука определяет количественную сторону общественного явления, наблюдает закономерности перехода количества в качество на примере данного общественного явления и на основании этих наблюдений производит анализ данных, полученных в определенных условиях места и времени. Статистика исследует социально-экономические явления и процессы, которые носят массовый характер, изучает множество определяющих их факторов.

Большинство общественных наук пользуются статистикой для выведения и подтверждения своих теоретических законов. Выводами, основанными на статистических исследованиях, пользуются экономика, история, социология, политология и многие другие гуманитарные науки. Статистика необходима не только общественным наукам для подтверждения их теоретической основы, но велика и практическая ее роль: ни одно крупное предприятие или серьезное производство, разрабатывая стратегию экономического и социального развития объекта, не может обойтись без анализа данных статистического учета. Для этого на предприятиях создаются специальные аналитические отделы и службы, которые привлекают специалистов, прошедших профессиональную подготовку по данной дисциплине.

Как любая наука, статистика имеет определенную методологию изучения своего предмета. Как уже отмечалось выше, ее в основном интересует развитие явления и его связь с другими явлениями общественной жизни, поэтому метод статистики выбирается в зависимости от изучаемого явления и конкретного предмета изучения. В статистике разработаны и применяются специфические способы и приемы исследования общественных явлений, которые в совокупности и образуют метод статистики. К ним относятся наблюдение, сводка и группировка данных, исчисление обобщающих показателей на основе специальных методов (метод средних индексов и т. д.). В соответствии с вышесказанным различают три этапа работы со статистическими данными:

• сбор;

• группировка и сводка;

• обработка и анализ.

Под сбором данных понимают массовое научно-организованное наблюдение, посредством которого получают первичную информацию об отдельных фактах (единицах) исследуемого явления. Такой статистический учет большого числа или всех входящих в состав изучаемого явления единиц является информационной базой для статистических обобщений, для формулирования выводов об изучаемом явлении или процессе. Под группировкой и сводкой данных понимают распределение множества фактов (единиц) на однородные группы и подгруппы, подсчет итогов по каждой группе и подгруппе и оформление полученных итогов в виде статистической таблицы.

Статистический анализ является заключительной стадией статистического исследования. Он включает в себя обработку статистических данных, полученных при сводке, интерпретацию полученных результатов с целью получения объективных выводов о состоянии изучаемого явления и закономерностях его развития. В процессе статистического анализа изучаются структура, динамика и взаимосвязь общественных явлений и процессов.

К основным этапам статистического анализа относят:

• установление фактов и их оценку;

• выявление характерных особенностей и причин явления;

• сопоставление явления с нормативными, плановыми и прочими явлениями, принятыми за базу сравнения;

• формулирование выводов, прогнозов, предположений и гипотез;

• статистическую проверку выдвинутых гипотез.

Основные положения статистики, с одной стороны, базируются на законах социальной и экономической теории, так как именно они рассматривают закономерности развития общественных явлений, определяют их значение, причины и последствия для жизни общества. С другой стороны, законы многих общественных наук построены на основании показателей статистики и закономерностей, определенных с помощью статистического анализа. Таким образом, статистика определяет законы общественных наук, а они в свою очередь корректируют положения статистики. Теоретическая основа статистики тесно связана с математикой, так как для измерения, сравнения и анализа количественных характеристик необходимо применять математические показатели, законы и методы: изучение динамики явления, его взаимосвязи с другими явлениями невозможно без применения высшей математики и математического анализа.

Очень часто статистическое исследование опирается на разработанную математическую модель явления. Такая мо-

дель теоретически отражает количественные соотношения изучаемого явления.

Так, например, при оценке финансового состояния предприятия часто используют скоринговую модель А. Альтмана, где уровень банкротства Z вычисляется по следующей формуле:

Z = 1,2x1 + 1,4x2 + 3,3x3 + 0,6x4 + 10,0x5.

По оценке Альтмана, при Z ‹2,675 фирме грозит банкротство, а при Z › 2,675 финансовое положение фирмы не внушает опасений. Чтобы получить эту оценку, надо подставить в формулу неизвестные ?1, ?2, ?3, ?4 и ?5 , которые являются определенными показателями строк баланса.

Особенно большое распространение в статистической науке получили такие направления математики, как теория вероятностей и математическая статистика. Широко применяется ряд теорем, выражающих закон больших чисел, анализ вариационных рядов, прогнозирование развития явлений осуществляется с помощью экстраполяций. Причинно-следственные связи явлений и процессов устанавливаются с помощью корреляционного и регрессионного анализа. Наконец, статистическая наука обязана математической статистике такими важнейшими своими категориями и понятиями, как совокупность, вариация, признак, закономерность.

Статистическая совокупность относится к основным категориям статистики и является объектом статистического исследования, под которым понимается планомерный научно-обоснованный сбор сведений о социально-экономических явлениях общественной жизни и анализ полученных данных. Для того чтобы выполнить статистическое исследование, необходима научно обоснованная информационная база, которой и является статистическая совокупность – совокупность социально-экономических объектов или явлений общественной жизни, объединенных качественной основой, общей связью, но отличающихся друг от друга отдельными признаками, например совокупность до-мохозяйств, семей, фирм и т. д.

С точки зрения статистической методологии статистическая совокупность – это множество единиц, обладающих такими характеристиками, как массовость, однородность, определенная целостность, взаимозависимость состояния отдельных единиц, наличие вариации. Единицей совокупности может выступать предмет, факт, человек, процесс и т. п. Единица совокупности является первичным элементом и носителем ее основных признаков. Элемент совокупности, по которому собираются необходимые данные для статистического исследования, называется единицей наблюдения. Количество единиц совокупности называется объемом совокупности.

Статистической совокупностью может быть население при переписи, предприятия, города, сотрудники фирмы. Выбор статистической совокупности и ее единиц зависит от конкретных условий и характера изучаемого социально-экономического явления, процесса.

Массовость единиц совокупности тесно связана с полнотой совокупности, которая обеспечивается охватом единиц исследуемой статистической совокупности. Например, исследователь должен сделать вывод о развитии банковского дела. Следовательно, ему необходимо собрать информацию обо всех банках, действующих в данном регионе. Так как любая совокупность имеет достаточно сложный характер, то полноту следует понимать, как и охват множества самых различных признаков совокупности, достоверным и существенным образом описывающих изучаемое явление. Если в процессе наблюдения за банками, например, не будут учтены финансовые результаты, то нельзя сделать окончательные выводы о развитии банковской системы. Кроме того, полнота предполагает изучение признаков единиц совокупности за максимально длительные периоды. Достаточно полные данные являются, как правило, массовыми, исчерпывающими.

На практике исследуемые социально-экономические явления чрезвычайно многообразны, поэтому охватить все явления сложно и подчас невозможно. Исследователь вынужден изучать лишь часть статистической совокупности, а выводы делать по всей совокупности. В таких ситуациях важнейшим требованием является обоснованный отбор той части совокупности, по которой изучаются признаки. Эта часть должна отражать основные свойства явления и быть типичной. В реальной действительности в изучаемых явлениях и процессах могут взаимодействовать несколько совокупностей. В этих ситуациях в объекте изучения должны четко выделяться исследуемые совокупности.

Признаком единицы совокупности называют характерную черту, особенность, конкретное свойство, качество, которое может быть наблюдаемо и измерено. Совокупность, изучаемая во времени или в пространстве, должна быть сопоставима. Для этого необходимо использовать, например, единые стоимостные оценки. Для того чтобы качественно исследовать совокупность, изучают наиболее существенные или взаимосвязанные признаки. Количество признаков, характеризующих единицу совокупности, не должно быть излишним, так как это усложняет сбор данных и обработку результатов. Признаки единиц статистической совокупности необходимо комбинировать так, чтобы они дополняли друг друга и обладали взаимозависимостью.

Требование однородности статистической совокупности означает выбор критерия, по которому та или иная единица относится к изучаемой совокупности. Например, если изучается активность молодых избирателей, то необходимо определить границы возраста таких избирателей, чтобы исключить людей более старшего поколения. Можно ограничить такую совокупность представителями сельской местности или, например, студенчества.

Наличие вариации у единиц совокупности означает, что их признаки могут принимать различные значения или видоизменения. Такие признаки называются варьирующими, а отдельные значения или видоизменения – вариантами.

Признаки делятся на атрибутивны1е и количественные. Признак называется атрибутивным, или качественным, если он выражается смысловым понятием, например пол человека или его принадлежность к той либо иной социальной группе. Внутри они подразделяются на номинальные и порядковые.

Признак называют количественным, если он выражен числом. По характеру варьирования количественные признаки делятся на дискретные и непрерывные. Дискретные признаки обычно выражаются в виде целых чисел, например число человек в семье. К непрерывным признакам относятся, например, возраст, величина заработной платы, стаж работы и т. д.

По способу измерения признаки делятся на первичные (учитываемые) и вторичные (расчетные). Первичные (учитываемые) выражают единицу совокупности в целом, т. е. абсолютные величины. Вторичные (расчетные) непосредственно не измеряются, а рассчитываются (себестоимость, производительность). Первичные признаки лежат в основе наблюдения статистической совокупности, а вторичные определяются в процессе обработки и анализа данных и представляют собой соотношение первичных признаков.

По отношению к характеризуемому объекту признаки делятся на прямые и косвенные. Прямые признаки – это свойства, непосредственно присущие характерному объекту (объем продукции, возраст человека). Косвенные признаки являются свойствами, присущими не самому объекту, а другим совокупностям, относящимся к объекту или входящим в него.

По отношению ко времени различают моментальные и интервальные признаки. Моментальные признаки характеризуют изучаемый объект в какой-то момент времени, установленный планом статистического исследования. Интервальные признаки характеризуют результаты процессов. Их значения могут возникать только за определенный интервал времени.

Кроме признаков состояние исследуемого объекта или статистической совокупности характеризуют показатели. Показатели – одно из основных понятий статистики, под которым понимается обобщенная количественная оценка социально-экономических явлений и процессов. В зависимости от целевых функций статистические показатели делятся на учетно-оценочные и аналитические. Учетно-оце-ночные показатели – это статистическая характеристика размеров социально-экономических явлений в определенных условиях места и времени, отображающая объемы распространения явлений в пространстве или достигнутые на определенное время уровни. Аналитические показатели применяются для анализа данных изучаемой статистической совокупности и характеризуют особенности развития исследуемых явлений. В качестве аналитических показателей в статистике применяются относительные, средние величины, показатели вариации и динамики, показатели связи. Совокупность статистических показателей, отражающих взаимосвязи, которые существуют между явлениями, образуют системыг статистических показателей.

В целом показатели и признаки в полной мере характеризуют и исчерпывающим образом описывают статистическую совокупность, позволяя исследователю проводить всестороннее изучение явлений и процессов жизни человеческого общества, что и является одной из целей статистической науки.

Важнейшей категорией статистики является статистическая закономерность. Под закономерностью вообще понимают обнаруживаемую причинно-следственную связь между явлениями, последовательность и повторяемость отдельных признаков, характеризующих явление. В статистике же под закономерностью понимают количественную закономерность изменения в пространстве и времени массовых явлений и процессов общественной жизни в результате действия объективных законов. Следовательно, статистическая закономерность свойственна не отдельным единицам совокупности, а всей совокупности в целом и проявляется только при достаточно большом числе наблюдений. Таким образом, статистическая закономерность обнаруживает себя как средняя, общественная, массовая закономерность при взаимопогашении индивидуальных отклонений значений признаков в ту или иную сторону. Проявление статистической закономерности дает возможность представить общую картину явления, изучить тенденцию его развития, исключая случайные, индивидуальные отклонения.

Статистика играет важную роль в управлении экономическим и социальным развитием страны, так как правильность любого управленческого решения во многом зависит от той информации, на основе которой оно принято. Только точные, достоверные и правильно проанализированные данные должны приниматься во внимание на высоких уровнях управления.

Изучением экономического и социального развития страны, отдельных регионов, отраслей, фирм, предприятий занимаются специально созданные для этого органы, образующие статистическую службу. В Российской Федерации функции статистической службы выполняют органы государственной статистики и органы ведомственной статистики.

Высшим органом управления статистикой в нашей стране является Федеральная служба государственной статистики (ФСГС), созданная в соответствии с Указом Президента РФ от 09.03.2004 № 314 «Структура федеральных органов исполнительной власти». ФСГС является федеральным органом исполнительной власти, осуществляющим функции по формированию официальной статистической информации о социальном, экономическом, демографическом и экологическом положении страны, а также функции по контролю и надзору в области государственной статистической деятельности на территории РФ.

Федеральная служба государственной статистики находится в ведении Министерства экономического развития и торговли РФ.

Согласно постановлению Правительства РФ от 07.04.2004 № 188 основными функциями Федеральной службы государственной статистики являются:

• представление в установленном порядке статистической информации Президенту РФ, Правительству РФ, Федеральному Собранию РФ, органам государственной власти, средствам массовой информации, организациям и гражданам, а также международным организациям;

• разработка и совершенствование научно обоснованной официальной статистической методологии для проведения статистических наблюдений и формирования статистических показателей, обеспечение соответствия указанной методологии международным стандартам;

• разработка и совершенствование системы статистических показателей, характеризующих состояние экономики и социальной сферы;

• сбор статистической отчетности и формирование на ее основе официальной статистической информации;

• контроль за выполнением организациями и гражданами, осуществляющими предпринимательскую деятельность без образования юридического лица, законодательства РФ в области государственной статистики;

• развитие информационной системы государственной статистики, обеспечение ее совместимости и взаимодействия с другими государственными информационными системами;

• обеспечение хранения государственных информационных ресурсов и защиты конфиденциальной и отнесенной к государственной тайне статистической информации;

• реализация обязательств РФ, вытекающих из членства в международных организациях и участия в международных договорах, осуществление международного сотрудничества в области статистики.

Методология статистических показателей, формы и методы сбора и обработки статистических данных, установленные ФСГС, являются официальными статистическими стандартами РФ.

В своей основной деятельности ФСГС руководствуется федеральными статистическими программами, которые формируются с учетом предложений федеральных органов исполнительной и законодательной власти, органов государственной власти субъектов РФ, научных и других организаций и утверждаются ФСГС по согласованию с Правительством РФ.

Основной задачей статистических органов страны является обеспечение гласности и доступности общей (не индивидуальной) информации, а также гарантия достоверности, точности и правдивости учтенных данных. Кроме того, задачами ФСГС являются:

• представление официальной статистической информации Президенту РФ, Правительству РФ, Федеральному Собранию РФ, федеральным органам исполнительной власти, общественности, а также международным организациям;

• координация статистической деятельности федеральных органов исполнительной власти и органов исполнительной власти субъектов РФ, обеспечение условий для использования указанными органами официальных статистических стандартов при проведении ими отраслевых (ведомственных) статистических наблюдений;

• разработка экономико-статистической информации, ее анализ, составление национальных счетов, необходимых балансовых расчетов;

• гарантирование полноты и научной обоснованности всей официальной статистической информации;

• предоставление всем пользователям равного доступа к открытой статистической информации путем распространения официальных докладов о социально-экономическом положении Российской Федерации, субъектов РФ, отраслей и секторов экономики, публикации статистических сборников и других статистических материалов.

В результате реформирования экономики РФ изменилась и структура органов статистики. Местные районные статистические регистратуры упразднены и образованы межрайонные отделы статистики, которые являются представительствами территориальных органов статистики. Организация статистических органов России сейчас находится на стадии реформирования. На рис. 1.2 представлена схема органов статистики РФ на 2004 г.

Рис. 1.2. Схема органов статистики Российской Федерации на 2004 г.

В настоящее время можно отметить основные направления, по которым должны быть произведены реформы:

• соблюдение основного закона статистического учета – гласности и доступности информации при сохранении конфиденциальности индивидуальных показателей (коммерческой тайны);

• реформирование методологических и организационных основ статистики: изменение общих задач и принципов ведения хозяйства приводит к изменению теоретических положений науки;

• совершенствование системы сбора и обработки информации путем введения таких форм наблюдения, как цензы, регистры (реестры), переписи и др.;

• изменение (усовершенствование) методологии исчисления некоторых статистических показателей, характеризующих состояние экономики РФ, с учетом международных стандартов, иностранного опыта ведения статистического учета, систематизация всех показателей и приведение их в порядок, отвечающий вопросам и требованиям времени, с учетом системы национальных счетов (СНС);

• обеспечение взаимосвязи статистических показателей, характеризующих уровень развития общественной жизни страны;

• учет тенденции компьютеризации.

В ходе реформирования статистической науки должна быть создана единая информационная база (система), которая будет включать в себя информационные базы всех статистических органов, находящихся на более низкой ступени иерархической лестницы организации государственной статистики. В настоящее время проведена большая работа по организации работы статистических органов, но она еще не закончена, и предстоит еще много внимания уделить совершенствованию этого очень важного для государства информационного института.

Наряду с государственными статистическими службами существует ведомственная статистика, которая ведется в министерствах, ведомствах, на предприятиях, в объединениях и фирмах различных отраслей экономики. Ведомственная статистика занимается сбором, обработкой и анализом статистической информации, необходимой для руководства, принятия управленческих решений, планирования деятельности предприятия или органа власти. На небольших предприятиях этой работой, как правило, занимается либо главный бухгалтер, либо непосредственно сам руководитель. На крупных предприятиях с разветвленной собственной региональной структурой или большой численностью, на крупных производствах организуются целые отделы или управления, занимающиеся анализом статистической информации. К этой работе привлекаются специалисты в области статистики, математики, бухгалтерского учета и экономического анализа, менеджеры и технологи. Подобная «команда», вооруженная современными средствами вычислительной техники, опираясь на методологию, предлагаемую теорией статистики и используя современные методики анализа, помогает строить эффективные стратегии развития бизнеса, а также эффективно организовывать деятельность органов государственной власти. Управлять сложными социальными и экономическими системами, не располагая оперативной, полной и достоверной статистической информацией, невозможно.

Таким образом, перед органами государственной и ведомственной статистикой стоит очень важная задача теоретического обоснования объема и состава статистической информации, которая соответствовала бы современным условиям развития экономики, способствовала рационализации в системе учета и статистики и минимизированию затрат на выполнение этой функции.

Глубокое всестороннее исследование любого экономического или социального процесса предполагает измерение его количественной стороны и характеристику его качественной сущности, места, роли и взаимосвязей в общей системе общественных отношений. Прежде чем приступить к использованию статистических методов изучения явлений и процессов общественной жизни, необходимо иметь в своем распоряжении исчерпывающую информационную базу, в полной мере и достоверно описывающую объект исследования. Процесс статистического исследования предполагает проведение следующих этапов:

• сбор статистической информации (статистическое наблюдение) и ее первичная обработка;

• систематизация и дальнейшая обработка данных, полученных в результате статистического наблюдения, на основе их сводки и группировки;

• обобщение и анализ результатов обработки статистических материалов, формулировка выводов и рекомендаций по итогам всего статистического исследования.

Статистическое наблюдение – первый и исходный этап статистического исследования, который представляет собой систематический, планомерно организуемый на научной основе процесс сбора первичных данных о различных явлениях социальной и экономической жизни. Планомерность статистического наблюдения заключается в том, что оно проводится по специально разработанному плану, который включает в себя вопросы, связанные с организацией и техникой сбора статистической информации, контроля ее качества и достоверности, представления итоговых материалов. Массовый характер статистического наблюдения обеспечивается наиболее полным охватом всех случаев проявления изучаемого явления или процесса, т. е. в процессе статистического наблюдения подвергаются измерению и регистрации количественные и качественные характеристики не отдельных единиц изучаемой совокупности, а всей массы единиц совокупности. Систематичность статистического наблюдения означает, что оно должно проводиться не случайным образом, т. е. стихийно, а выполняться либо непрерывно, либо регулярно через равные промежутки времени.

Процесс проведения статистического наблюдения представлен на рис. 2.1.

Рис. 2.1. Схема проведения статистического наблюдения

Процесс подготовки статистического наблюдения предполагает определение цели и объекта наблюдения, состава признаков, подлежащих регистрации, выбора единицы наблюдения. Также необходимо разработать бланки документов для сбора данных и выбрать средства и методы их получения.

Таким образом, статистическое наблюдение представляет собой трудоемкую и кропотливую работу, требующую привлечения квалифицированных кадров, всесторонне продуманной ее организации, планирования, подготовки и проведения.

Задачей общей теории статистики является определение форм, видов и способов статистического наблюдения для решения вопроса, где, когда и какие приемы наблюдения применять. Приведенная ниже схема иллюстрирует классификацию видов статистического наблюдения (рис. 2.2).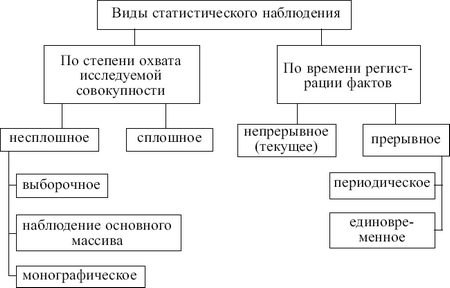

Рис. 2.2. Классификация видов статистического наблюдения

Статистические наблюдения можно разбить на группы:

• по охвату единиц совокупности;

• времени регистрации фактов.

По степени охвата исследуемой совокупности статистическое наблюдение подразделяется на два вида: сплошное и несплошное. При сплошном (полном) наблюдении охватываются все единицы изучаемой совокупности. Сплошное наблюдение обеспечивает полноту информации об изучаемых явлениях и процессах. Такой вид наблюдения связан с большими затратами трудовых и материальных ресурсов, так как для сбора и обработки всего объема необходимой информации требуется значительное время. Часто сплошное наблюдение вообще невозможно, например, когда обследуемая совокупность слишком велика или отсутствует возможность получения информации обо всех единицах совокупности. По этой причине проводят несплошные наблюдения.

При несплошном наблюдении охватывается только определенная часть изучаемой совокупности, при этом важно заранее определить, какая именно часть изучаемой совокупности будет подвергнута наблюдению и какой критерий будет положен в основу выборки. Преимущество проведения несплошного наблюдения заключается в том, что оно проводится в короткие сроки, связано с меньшими трудовыми и материальными затратами, полученная информация носит оперативный характер. Существует несколько видов несплошного наблюдения: выборочное, наблюдение основного массива, монографическое.

Выборочным называют наблюдение части единиц исследуемой совокупности, выделенной методом случайного отбора. При правильной организации выборочное наблюдение дает достаточно точные результаты, которые можно применить с определенной вероятностью на всю совокупность. Если выборочное наблюдение предполагает отбор не только единиц изучаемой совокупности (выборку в пространстве), но и моментов времени, в которые проводится регистрация признаков (выборка во времени), такое наблюдение называется методом моментных наблюдений.

Наблюдение основного массива охватывает собой обследование определенных, наиболее существенных по значимости изучаемых признаков единиц совокупности. При этом наблюдении в учет принимаются самые крупные единицы совокупности, а регистрируются самые существенные для данного исследования признаки. Например, обследуются 15–20 % крупных кредитных учреждений, при этом регистрируется содержание их инвестиционных портфелей.

Для монографического наблюдения характерно всестороннее и глубокое изучение лишь отдельных единиц совокупности, обладающих какими-либо особенными характеристиками или представляющими какое-либо новое явление. Цель такого наблюдения – выявление имеющихся или только зарождающихся тенденций в развитии данного процесса или явления. При монографическом обследовании отдельные единицы совокупности подвергаются детальному изучению, которое позволяет зафиксировать очень важные зависимости и пропорции, которые не обна-ружимы при других, не столь подробных, наблюдениях. Статистико-монографическое обследование часто применяется в медицине, при обследовании бюджетов семей и т. д. Важно отметить, что монографическое наблюдение тесно связано со сплошным и выборочным наблюдениями. Во-первых, данные массовых обследований необходимы для выбора критерия отбора единиц совокупности для проведения несплошного и монографического наблюдения. Во-вторых, монографическое наблюдение позволяет выявить характерные черты и существенные признаки объекта исследования, уточнить структуру изучаемой совокупности. Полученные выводы можно положить в основу организации нового массового обследования.

По времени регистрации фактов наблюдение может быть непрерывным и прерывным. Прерыывное в свою очередь включает периодическое и единовременное. Непре-рыгвное (текущее) наблюдение осуществляется путем непрерывной регистрации фактов по мере их возникновения. При таком наблюдении прослеживаются все изменения изучаемого процесса или явления, что позволяет следить за его динамикой. Непрерывно ведется, например, регистрация органами записи актов гражданского состояния (ЗАГСа) смертей, рождений, браков. На предприятиях ведется текущий учет производства продукции, отпуска материалов со склада и т. д.

Прерыгвное наблюдение проводится либо регулярно, через определенные промежутки времени (периодическое наблюдение), либо нерегулярно, однократно, по мере необходимости (единовременное наблюдение). В основу периодических наблюдений, как правило, заложены подобные программа и инструментарий, с тем чтобы результаты таких обследований могли быть сопоставимы. Примером периодического наблюдения может являться перепись населения, которая проводится через достаточно длительные промежутки времени, и все формы статистических наблюдений, которые носят ежемесячный, квартальный, полугодовой, годовой и т. д. характер. Единовременное наблюдение характерно тем, что факты регистрируются не в связи с их возникновением, а по состоянию или наличию их на определенный момент или за период времени. Количественное измерение признаков какого-либо явления или процесса происходит в момент проведения обследования, а повторная регистрация признаков может не производиться вообще или сроки ее проведения заранее не определены. Примером единовременного наблюдения может служить единовременное обследование состояния жилищного строительства, которое проводилось в 2000 г.

Наряду с видами статистического наблюдения в общей теории статистики рассматриваются способы получения статистической информации, важнейшими из которых являются документальный способ наблюдения, способ непосредственного наблюдения, опрос.

Документальное наблюдение основано на использовании в качестве источника информации данных различных документов, например регистров бухгалтерского учета. Учитывая, что к заполнению таких документов, как правило, предъявляются высокие требования, данные, отраженные в них, носят наиболее достоверный характер и могут служить качественным исходным материалом для проведения анализа.

Непосредственное наблюдение осуществляется путем регистрации фактов, лично установленных регистраторами в результате осмотра, измерения, подсчета признаков изучаемого явления. Таким способом регистрируются цены на товары и услуги, производятся замеры рабочего времени, инвентаризация остатков на складе и т. д.

Опрос базируется на получении данных от респондентов (участников опроса). Опрос применяют в тех случаях, когда наблюдение другими способами не может быть осуществлено. Такой вид наблюдения характерен для проведения различных социологических обследований и опросов общественного мнения. Статистическая информация может быть получена разными видами опросов: экспедиционным, корреспондентским, анкетным, явочным.

Экспедиционными (устный) опрос проводится специально подготовленными работниками (регистраторами), которые фиксируют ответы респондентов в формулярах наблюдения. Формуляр представляет собой бланк документа, в котором необходимо заполнить поля для ответов.

Корреспондентский опрос предполагает, что на добровольной основе штат респондентов сообщает сведения непосредственно в орган, ведущий наблюдение. Недостатком этого способа является то, что затруднительно проверить правильность полученной информации.

При анкетном опросе респонденты заполняют анкеты (вопросники), добровольно и преимущественно анонимно. Поскольку этот способ получения информации не является надежным, его применяют в тех исследованиях, где не требуется высокая точность результатов. В некоторых ситуациях бывает достаточно приближенных результатов, которые улавливают лишь тенденцию и фиксируют появление новых фактов и явлений. Явочный опрос предполагает представление сведений в органы, ведущие наблюдение, в явочном порядке. Таким способом регистрируются акты гражданского состояния: браки, разводы, смерти, рождения и т. д.

Кроме видов и способов статистического наблюдения в теории статистики рассматриваются и формы статистического наблюдения: отчетность, специально организованное статистическое наблюдение, регистры.

Статистическая отчетносты – основная форма статистического наблюдения, которая характеризуется тем, что сведения об изучаемых явлениях статистические органы получают в виде особых документов, представляемых предприятиями и организациями в определенные сроки и по установленной форме. Сами формы статистической отчетности, методы сбора и обработки статистических данных, методология статистических показателей, установленные ФСГС, являются официальными статистическими стандартами РФ и обязательны для всех субъектов общественных отношений.

Статистическую отчетность делят на специализированную и типовую. Состав показателей типовой отчетности един для всех предприятий и организаций, в то время как состав показателей специализированной отчетности зависит от специфики отдельных отраслей экономики и сферы

деятельности. По срокам представления статистическая отчетность бывает ежедневная, недельная, декадная, двухнедельная, месячная, квартальная, полугодовая и годовая. Статистическая отчетность может передаваться по телефону, каналам связи, на электронных носителях с обязательным последующим представлением на бумажных носителях, скрепленная подписью ответственных лиц.

Специально организованное статистическое наблюдение представляет собой организуемый статистическими органами сбор сведений или для изучения явлений, не охватываемых отчетностью, или для более глубокого изучения отчетных данных, их проверки и уточнения. Различного рода переписи, единовременные обследования являются специально организованными наблюдениями.

Регистры – это такая форма наблюдения, при которой факты состояния отдельных единиц совокупности непрерывно регистрируются. Наблюдая за единицей совокупности, предполагают, что происходящие там процессы имеют начало, долговременное продолжение и конец. В регистре каждая единица наблюдения характеризуется совокупностью показателей. Все показатели хранятся до тех пор, пока единица наблюдения находится в регистре и не закончила своего существования. Некоторые показатели остаются неизменными все время, пока единица наблюдения находится в регистре, другие могут меняться время от времени. Примером такого регистра может служить Единый государственный регистр предприятий и организаций (ЕГРПО). Все работы по его ведению осуществляет ФСГС.

Итак, выбор видов, способов и форм статистического наблюдения зависит от целого ряда факторов, основными из которых являются цели и задачи наблюдения, специфика наблюдаемого объекта, срочность представления результатов, наличие подготовленных кадров, возможность применения технических средств сбора и обработки данных.

Одной из важнейших задач, которую необходимо решить при подготовке статистического наблюдения, является определение цели, объекта и единицы наблюдения.

Целы практически любого статистического наблюдения – получение достоверной информации о явлениях и процессах общественной жизни, с тем чтобы выявить взаимосвязи факторов, оценить масштабы явления и закономерности его развития. Исходя из задач наблюдения, определяются его программа и формы организации. Кроме цели следует установить объект наблюдения, т. е. определить, что именно подлежит наблюдению.

Объектом наблюдения называется совокупность общественных явлений или процессов, подлежащих исследованию. Объектом наблюдения может быть совокупность учреждений (кредитные, образовательные и т. п.), население, физические объекты (здания, транспорт, техника). При установлении объекта наблюдения важно строго и точно определить границы изучаемой совокупности. Для этого необходимо четко установить существенные признаки, по которым определяют: включать объект в совокупность или нет. Например, прежде чем проводить обследование медицинских учреждений на предмет оснащенности современным оборудованием, следует определить категорию, ведомственную и территориальную принадлежность подлежащих обследованию клиник. Определяя объект наблюдения, необходимо указать единицу наблюдения и единицу совокупности.

Единицей наблюдения является составной элемент объекта наблюдения, представляющий собой источник информации, т. е. единица наблюдения является носителем признаков, подлежащих регистрации. В зависимости от конкретных задач статистического наблюдения это может быть домашнее хозяйство или человек, например учащийся, предприятие сельского хозяйства или завод. Единицы наблюдения называют отчетными единицами, если они представляют статистическую отчетность в статистические органы.

Единица совокупности – это составной элемент объекта наблюдения, от которого поступают сведения о единице наблюдения, т. е. единица совокупности служит основой счета и обладает признаками, подлежащими регистрации в процессе наблюдения. Например, при переписи лесных насаждений единицей совокупности будет дерево, так как оно обладает признаками, подлежащими регистрации (возраст, породный состав и т. п.), в то время как само лесное хозяйство, в котором ведется обследование, выступает единицей наблюдения.

Каждое явление или процесс общественной жизни обладает множеством признаков, но получить информацию обо всех невозможно, да и не все из них представляют интерес для исследователя, поэтому при подготовке наблюдения следует решить вопрос о том, какие признаки будут подлежать регистрации в соответствии с целями и задачами наблюдения. Для определения состава регистрируемых признаков разрабатывают программу наблюдения.

Программой статистического наблюдения называют совокупность вопросов, ответы на которые в процессе наблюдения и должны составить статистические сведения. Разработка программы наблюдения – очень важная и ответственная задача, и от того, насколько правильно она будет выполнена, зависит успех проведения наблюдения. При разработке программы наблюдения необходимо учитывать ряд предъявляемых к ней требований:

• программа должна по возможности содержать только те признаки, которые необходимы и значения которых будут использованы для проведения дальнейшего анализа или в контрольных целях. Стремясь к полноте сведений, обеспечивающих получение доброкачественных материалов, следует ограничить объем собираемой информации, чтобы получить достоверный материал для анализа;

• вопросы программы должны быть сформулированы четко, чтобы исключить неправильную их трактовку и не допустить искажение смысла собираемой информации;

• при разработке программы наблюдения желательно выстроить логичную последовательность вопросов; однотипные вопросы или признаки, характеризующие какую-либо одну сторону явления, следует объединять в один раздел;

• программа наблюдения должна содержать контрольные вопросы для проверки и корректировки регистрируемых сведений.

Для проведения наблюдения необходим определенный инструментарий: формуляры и инструкции. Статистический формуляр – специальный документ единого образца, в котором фиксируются ответы на вопросы программы. В зависимости от конкретного содержания проводимого наблюдения формуляр может называться формой статистической отчетности, переписным или опросным листом, картой, карточкой, анкетой или бланком. Различают два вида формуляров: карточный и списочный. Формуляр-карточка, или индивидуальный формуляр, предназначен для отражения сведений об одной единице статистической совокупности, а списочный формуляр содержит сведения о нескольких единицах совокупности. Неотъемлемыми и обязательными элементами статистического формуляра являются титульная, адресная и содержательная части. В титулыной части указывается наименование статистического наблюдения и органа, который утвердил этот формуляр, сроки представления формуляра и некоторая другая информация. В адресной части указываются реквизиты отчитывающейся единицы наблюдения. Основная, содержателыная, часть формуляра обычно выглядит в форме таблицы, которая содержит наименование, коды и значения показателей.

Заполнение статистического формуляра происходит в соответствии с инструкцией. Инструкция содержит указания о порядке проведения наблюдения, методические указания и разъяснения по заполнению формуляра. В зависимости от сложности программы наблюдения инструкция публикуется либо в виде брошюры, либо помещается на обратной стороне формуляра. Кроме того, за необходимыми разъяснениями можно обратиться к специалистам, ответственным за проведение наблюдения, в органы, которые его проводят.

При организации статистического наблюдения необходимо решить вопрос о времени наблюдения и месте его проведения. Выбор места проведения наблюдения зависит от цели наблюдения. Выбор времени наблюдения связан с определением критического момента (даты) либо интервала времени и определение срока (периода) наблюдения. Критическим моментом статистического наблюдения называют момент времени, к которому приурочены регистрируемые в процессе наблюдения сведения. Сроком наблюдения определяется период, в течение которого должна осуществляться регистрация сведений об изучаемом явлении, т. е. интервал времени, в течение которого заполняются формуляры. Обычно срок наблюдения должен быть не слишком удален от критического момента наблюдения, чтобы можно было воспроизвести состояние объекта на тот момент.

Для успешной подготовки и проведения статистического наблюдения должны быть решены вопросы организационного обеспечения. Для этого составляется организационный план наблюдения, в котором отражаются цели и задачи наблюдения, объект наблюдения, место, время, сроки наблюдения, круг лиц, отвечающих за проведение наблюдения.

Обязательным элементом организационного плана является указание органа наблюдения. Также определяется круг организаций, призванных оказывать содействие в проведении наблюдения, к ним могут относиться органы внутренних дел, налоговая инспекция, отраслевые министерства, общественные организации, физические лица, волонтеры и т. д.

В число подготовительных мероприятий входят:

• разработка формуляров статистического наблюдения, размножение документации самого обследования;

• разработка методологического аппарата для анализа и представления результатов наблюдения;

• разработка программного обеспечения для обработки данных, закупка вычислительной и оргтехники;

• закупка необходимых материалов, в том числе канцтоваров;

• подготовка квалифицированных кадров, обучение персонала, проведение различного рода инструктажа и т. д.;

• проведение массовой разъяснительной работы среди населения и участников наблюдения (лекции, беседы, выступления в печати, по радио и телевидению);

• согласование деятельности всех служб и привлекаемых к совместным действиям организаций;

• оборудование места сбора и обработки данных;

• подготовка каналов передачи информации и средств связи;

• решение вопросов, связанных с финансированием статистического наблюдения.

Таким образом, план наблюдения содержит ряд мероприятий, направленных на успешное проведение работы по регистрации необходимых сведений.

Каждое конкретное измерение величины данных, осуществляемое в процессе наблюдения, дает, как правило, приближенное значение величины явления, в той или иной мере отличающееся от истинного значения этой величины. Степень соответствия действительной величине какого-либо показателя или признака, полученного по материалам наблюдения, называется точностыю статистического наблюдения. Расхождение между результатом наблюдения и истинным значением величины наблюдаемого явления называется ошибкой наблюдения.

В зависимости от характера, стадии и причин возникновения различают несколько типов ошибок наблюдения (табл. 2.1).

Таблица 2.1

Классификация ошибок наблюдения

По своему характеру ошибки делятся на случайные и систематические. Случайными называют ошибки, возникновение которых обусловлено действием случайных факторов. К ним относятся оговорки и описки опрашиваемого лица. Они могут быть направлены в сторону уменьшения или увеличения значения признака, на конечном результате они, как правило, не отражаются, так как взаимопогашаются при сводной обработке результатов наблюдения. Систематические ошибки имеют одинаковую тенденцию либо к уменьшению, либо к увеличению значения показателя признака. Это связано с тем, что измерения, например, производятся неисправным измерительным прибором или ошибки являются следствием неточной формулировки вопроса программы наблюдения и др. Систематические ошибки представляют большую опасность, так как в значительной мере искажают результаты наблюдения.

В зависимости от стадии возникновения различают ошибки регистрации; ошибки, возникающие в ходе подготовки данных к машинной обработке; ошибки, проявляющиеся в процессе обработки на вычислительной технике.

К ошибкам регистрации относятся те неточности, которые возникают при записи данных в статистический формуляр (первичный документ, бланк, отчет, переписной лист) или при вводе данных в вычислительную технику, искажение данных при передаче через линии связи (телефон, электронную почту). Часто ошибки регистрации возникают из-за несоблюдения формы бланка, т. е. запись произведена не в ту строку или графу документа. Случается и преднамеренное искажение значений отдельных показателей.

Ошибки при подготовке данных к машинной обработке или в процессе самой обработки возникают в вычислительных центрах или центрах подготовки данных. Возникновение таких ошибок связано с небрежным, неправильным, нечетким заполнением данных в формулярах, с физическим дефектом носителя данных, с потерей части данных из-за несоблюдения технологии хранения информационных баз либо определяются сбоями в работе оборудования.

Зная виды и причины возникновения ошибок наблюдения, можно в значительной мере снизить процент подобных искажений информации. Различают следующие виды ошибок:

ошибки измерения, связанные с определенными погрешностями, которые возникают при однократном статистическом наблюдении явления и процессов общественной жизни;

ошибки репрезентативности, возникающие в ходе несплошного наблюдения и связанные с тем, что сама выборка не репрезентативна, и результаты, полученные на ее основе, не могут распространяться на всю совокупность;

преднамеренные ошибки, возникающие из-за сознательного искажения данных с разными целями, среди которых желание приукрасить действительное состояние объекта наблюдения или, наоборот, показать неудовлетворительное состояние объекта (данное искажение информации является нарушением закона);

непреднамеренные ошибки, как правило, носящие случайный характер и связанные с низкой квалификацией работников, их невнимательностью или небрежностью. Часто такие ошибки связаны с субъективными факторами, когда люди дают неправильную информацию о своем возрасте, семейном положении, образовании, принадлежности к социальной группе и т. д. или просто забывают некоторые факты, сообщая регистратору информацию, которая только что возникла в памяти.

Желательно провести некоторые мероприятия, которые помогут предупредить, выявить и исправить ошибки наблюдения. К ним относятся:

• подбор квалифицированных кадров и качественное обучение персонала, связанного с проведением наблюдения;

• организация контрольных проверок правильности заполнения документов, сплошным или выборочным методом;

• арифметический и логический контроль полученных данных после завершения сбора материалов наблюдения.

Основными видами контроля достоверности данных являются синтаксический, логический и арифметический (табл. 2.2).

Таблица 2.2

Виды и содержание контроля

Синтаксический контроль означает проверку правильности структуры документа, наличия необходимых и обязательных реквизитов, полноту заполнения строк формуляров в соответствии с установленными правилами. Важность и необходимость синтаксического контроля объясняется применением для обработки данных вычислительной техники, сканеров, которые предъявляют жесткие требования к соблюдению правил заполнения формуляров.

Логическим контролем проверяются правильность записи кодов, соответствие их наименованиям и значениям показателей. Выполняется проверка необходимых взаимосвязей между показателями, сопоставляются ответы на различные вопросы и выявляются несовместимые сочетания. Для исправления ошибок, выявленных при логическом контроле, возвращаются к исходным документам и делают поправки.

При арифметическом контроле сравниваются полученные итоги с предварительно подсчитанными контрольными суммами по строкам и по графам. Довольно часто арифметический контроль основывается на зависимости одного показателя от двух или нескольких других, например является произведением других показателей. Если арифметический контроль итоговых показателей обнаружит, что данная зависимость не соблюдается, это будет свидетельствовать о неточности данных.

Таким образом, контроль достоверности статистической информации осуществляется на всех этапах проведения статистического наблюдения, начиная со сбора первичной информации и до этапа получения итогов.

Научно организованная обработка материалов статистического наблюдения по заранее разработанной программе включает в себя, кроме контроля данных, систематизацию, группировку данных, составление таблиц, получение итогов и производных показателей (средних и относительных величин) и т. д. Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные сведения об отдельных единицах изучаемого явления. В таком виде материал еще не характеризует явление в целом: не дает представления ни о величине (численности) явления, ни о его составе, ни о размере характерных признаков, ни о существе связей этого явления с другими явлениями и т. д. Возникает необходимость в специальной обработке статистических данных – сводке материалов наблюдения.

Сводка материалов наблюдения представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность, с целью обнаружения типичных черт и закономерностей, присущих изучаемому явлению в целом.

Статистическая сводка (простая сводка) в узком смысле слова представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения. Статистическая сводка (сложная сводка) в широком смысле слова включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей,

представление результатов группировки и сводки в виде статистических таблиц.

Правильная, научно организованная сводка, опираясь на предварительный глубокий теоретический анализ, позволяет получить все статистические итоги, отражающие важнейшие, характерные черты объекта исследования, измерить влияние различных факторов на результат и учесть все это в практической работе при составлении текущих и перспективных планов. Задача сводки – дать характеристику объекту исследования с помощью систем статистических показателей, выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на трех этапах:

• определение групп и подгрупп;

• определение системы показателей;

• определение видов таблиц.

На первом этапе осуществляется систематизация, группировка материалов, собранных при наблюдении. На втором этапе уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета. На третьем этапе исчисляются сами показатели, и обобщенные данные для наглядности и удобства представляются в таблицах, статистических рядах, графиках, диаграммах.

Перечисленные этапы сводки еще до начала ее проведения отражаются в специально составляемой программе. Программа статистической сводки содержит перечень групп, на которые целесообразно разделить совокупность, их границы в соответствии с группировочными признаками; систему показателей, характеризующих совокупность, и методику их расчета; систему макетов разработочных таблиц, в которых будут представлены итоги расчетов.

Наряду с программой существует план проведения сводки, который предусматривает ее организацию. План проведения сводки должен содержать указания о последовательности и сроках выполнения ее отдельных частей, об ответственных за ее выполнение, порядке изложения результатов, а также предусматривать координацию работы всех организаций, задействованных в ее проведении.

Предмет статистических исследований – массовые явления и процессы общественной жизни – обладают многочисленными признаками и свойствами. Обобщить статистические данные, раскрыть наиболее существенные особенности, формы развития массового явления в целом и отдельных его составляющих невозможно без определенных научных принципов обработки данных. Без преодоления индивидуального многообразия объектов статистического наблюдения общие закономерности развития явления или процесса в целом теряются в деталях и мелочах, отличающих каждый объект один от другого, а предельное обобщение влечет за собой извращенное представление о действительности. Для разделения совокупности единиц на однотипные группы статистика использует метод группировок.

Статистические группировки – первый этап статистической сводки, позволяющий выделить из массы исходного статистического материала однородные группы единиц, обладающих общим сходством в качественном и количественном отношениях. Важно понимать, что группировка – это не субъективный технический прием разделения совокупности на части, а научно обоснованный процесс разделения множества единиц совокупности по определенному признаку.

Основополагающим принципом применения метода группировок является всесторонний, глубокий анализ сущности и природы изучаемого явления, позволяющий определить его типические свойства и внутренние различия. Любая общая совокупность является комплексом частных совокупностей, каждая из которых объединяет явления особого типа, однокачественные в определенном отношении. Каждый тип (группа) имеет специфическую систему признаков с соответствующим уровнем их количественных значений. Установить, к какому типу, в какую частную совокупность нужно отнести группируемые единицы общей совокупности, возможно на основе правильного, четкого определения существенных признаков, по которым должна проводиться группировка. Это второе важное требование научно обоснованной группировки. Третье требование группировки основано на объективном, обоснованном установлении границ групп при условии, что образованные группы должны объединять однородные элементы совокупности, а сами группы (одна по отношению к другой) должны существенно различаться. В противном случае группировка теряет смысл.

Таким образом, на основе применения метода группировок определяются группы по принципу подобия и различия единиц совокупности. Подобие – это однородность единиц в определенных пределах (группах); различие – это их существенное расхождение по группам.

Итак, группировка – разделение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками. Разнообразие общественных явлений и целей их изучения делает возможным применение большого количества статистических группировок явлений и решение на этой основе самых различных конкретных задач. Основными задачами, решаемыми с помощью группировок, в статистике являются следующие:

• выделение в совокупности изучаемых явлений их социально-экономических типов;

• изучение структуры общественных явлений;

• выявление связей и зависимостей между общественными явлениями.

Все группировки, связанные с выделением в совокупности изучаемых явлений их социально-экономических типов, занимают в статистике центральное место. Эта задача имеет отношение к наиболее существенным, решающим сторонам общественной жизни, например группировка населения по социальному статусу, полу, возрасту, уровню образования, группировка предприятий и организаций по формам собственности, отраслевой принадлежности. Построение подобных группировок за продолжительные периоды позволяет проследить процесс развития социально-экономических отношений. Задача расчленения совокупности общественных явлений по их социально-экономическим типам решается с помощью построения типологических группировок.

Таким образом, типологическая группировка – это разделение качественно разнородной исследуемой совокупности на однородные группы единиц в соответствии с социально-экономическими типами. Примером типологической группировки является группировка по виду участвующих субъектов инновационной деятельности в одном из регионов, которые можно разделить на следующие основные группы взаимоотношений (табл. 3.1).

Таблица 3.1

Группировка субъектов инновационной деятельности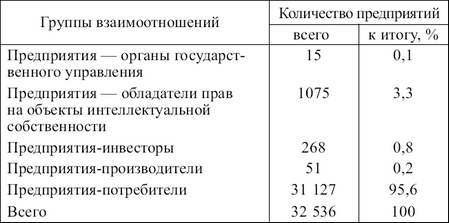

Исключительно важное значение придается изучению структуры общественных явлений, т. е. изучению различий в составе какого-либо определенного типа явлений (соотношения между составными частями явления, изменения в этих соотношениях за определенный период времени). Таким образом, структурной группировкой называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку. К структурным группировкам относятся группировка населения по полу, возрасту, уровню образования, группировка предприятий по численности работников, уровню заработной платы, объему работ и т. д. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития. Например, группировка в табл. 3.2 показывает, что в период с 1959 по 1994 г. численность городского населения постоянно увеличивалась, а численность сельского падала, однако в период с 1994 по 2002 г. соотношение этих групп населения не изменилось.

Таблица 3.2

Группировка населения России по месту проживания за 1959–2002 гг.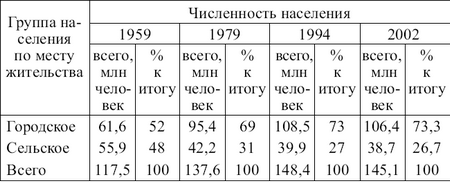

Применение структурных группировок позволяет не только раскрыть структуру совокупности, но и проанализировать изучаемые процессы, их интенсивность, изменение в пространстве, а взятые за ряд периодов времени структурные группировки раскрывают закономерности изменений состава совокупности во времени.

В основу структурных группировок могут быть положены атрибутивный или количественный признаки. Их выбор определяется задачами конкретного исследования и сущностью изучаемой совокупности. Группировка, приведенная в табл. 3.2, построена по атрибутивному признаку. При структурной группировке по количественному признаку возникает необходимость определения числа групп и их границ. Этот вопрос решается в соответствии с задачами исследования. Один и тот же статистический материал может быть разбит на группы различным образом в зависимости от целей и задач исследования. Главное, чтобы в процессе группировки были ярко отражены особенности изучаемого явления и созданы предпосылки для конкретных выводов и рекомендаций. В табл. 3.3 приведена структурная группировка по количественному признаку.

Таблица 3.3

Группировка семей жителей С.-Петербурга по величине среднедушевого дохода (по данным за сентябрь – октябрь 1996 г.)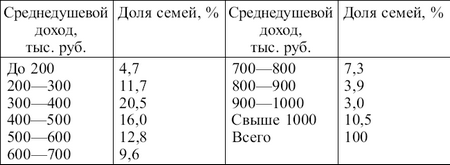

В данной таблице интервалы групп равны по своей величине. Если применяются равные интервалы, то расчет их величины производится по формуле

где h – величина интервала, xmax и xmin – максимальные и минимальные значения признаков совокупности, k – число групп.

Следует отметить, что технически удобнее иметь дело с равными интервалами, но это далеко не всегда представляется возможным из-за свойств изучаемых явлений и признаков. В экономике чаще приходится применять неравные, прогрессивно увеличивающиеся интервалы, что обусловлено самой природой экономических явлений.

Применение неравных интервалов объясняется главным образом тем, что абсолютное изменение группировочного признака на одну и ту же величину имеет далеко не одинаковое значение для групп с большим и малым значением признака. Например, между двумя предприятиями с численностью рабочих до 300 человек разница в 100 человек более существенна, чем для предприятий с численностью свыше 10 000 человек.

Интервалы групп могут быть замкнутыыми, когда указаны нижняя и верхняя границы, и открыгтыгми, когда указана лишь одна из границ групп. Открытые интервалы применяются только для крайних групп. При группировке с неравными интервалами желательно образование групп с замкнутыми интервалами. Это способствует точности статистических вычислений.

Одна из целей статистического наблюдения – выыявле-ние связей и зависимостей между общественными явлениями. Важной задачей статистического анализа, проводимого на основе типологической группировки, т. е. в пределах однокачественных совокупностей, является задача изучения и измерения связи между отдельными признаками. Установить факт наличия такой связи позволяет аналитическая группировка.

Аналитическая группировка – распространенный прием статистического изучения связей, которые обнаруживаются при параллельном сопоставлении обобщенных значений признаков по группам. Различают признаки зависимые, значения которых изменяются под влиянием других признаков, их обычно в статистике называют результативными, и факторные, оказывающие влияние на другие. Обычно в основе аналитической группировки лежит признак-фактор, а по результативным признакам производится расчет групповых средних, по изменению величины которых определяют наличие связи между признаками. Таким образом, аналитическими можно назвать такие группировки, которые позволяют установить и изучить связь между результативными и факторными признаками единиц однотипной совокупности.

Важная проблема аналитических группировок – правильный выбор числа групп и определение их границ, что в последующем обеспечивает объективность характеристик связи. Поскольку анализ ведется в однокачественных совокупностях, теоретических оснований для дробления определенного типа нет, поэтому допустима разбивка совокупности на любое число групп, удовлетворяющее определенным требованиям и условиям конкретного анализа. В процессе аналитических группировок следует соблюдать общие правила группировки, т. е. единицы в образованных группах должны быть существенно различны, количество единиц в группах должно быть достаточным для расчета надежных статистических характеристик. Кроме того, групповые средние должны подчиняться определенной закономерности: последовательно увеличиваться или уменьшаться.

Непосредственная группировка данных статистического наблюдения – это первичная группировка. Вторичная группировка – перегруппировка ранее сгруппированных данных. Необходимость вторичной группировки возникает в двух случаях:

• ранее произведенная группировка не удовлетворяет целям исследования в отношении числа групп;

• для сравнения данных, относящихся к различным периодам времени или к различным территориям, если первичная группировка была произведена по разным группи-ровочным признакам или по разным интервалам.

Существует два способа вторичной группировки:

• объединение мелких групп в более крупные;

• выделение определенной доли единиц совокупности.

В научно обоснованной группировке общественных явлений необходимо учитывать взаимозависимость явлений и возможность перехода постепенных количественных изменений в явлениях к коренным качественным изменениям. Группировка может быть научной лишь в том случае, если не только определены познавательные цели группировки, но и правильно выбрано основание группировки – группи-ровочный признак. Если группировка – это распределение на однородные группы по какому-либо признаку или объединение отдельных единиц совокупности в группы, однородные по какому-либо признаку, то группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в отдельные группы.

При выборе группировочного признака важным является не способ выражения признака, а его значение для изучаемого явления. С этой точки зрения для группировки следует брать существенные признаки, выражающие наиболее характерные черты изучаемого явления.

Самая простая группировка – ряд распределения. Рядами распределения называются ряды чисел (цифр), характеризующие состав или структуру какого-либо явления после группировки статистических данных об этом явлении, другими словами, это группировка, в которой для характеристики групп применяется один показатель – численность группы. Пример использование ряда распределения приведен в табл. 3.4.

Таблица 3.4

Применение рядов распределения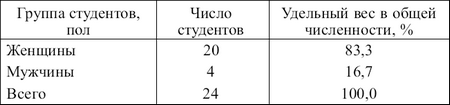

Приведенный ряд распределения содержит три элемента: разновидность атрибутивного признака (мужчины, женщины); численность единиц в каждой группе, называемая частотами ряда распределения; численность групп, выраженная в долях (процентах) от общей численности единиц, называемая частостями. Сумма частостей равна 1, если они выражены в долях единицы, и равна 100 %, если они выражены в процентах.

Ряды, построенные по атрибутивному признаку, называют атрибутивными.

Ряды распределения, построенные по количественному признаку, называются вариационныыми рядами. Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Вариационные ряды делятся на дискретные и интервальные.

Дискретныге вариационныге рядыг характеризуют распределение единиц совокупности по дискретному (прерывному) признаку, т. е. принимающему целые значения. При построении ряда распределения с дискретной вариацией признака все варианты выписываются в порядке возрастания их величины, подсчитывается, сколько раз повторяется одна и та же величина варианта, т. е. частота, и записывается в одной строке с соответствующим значением варианта, например распределение семей по числу детей (табл. 3.5).

Частоты в дискретном вариационном ряду, как и в атрибутивном, могут быть заменены частостями.

Таблица 3.5

Применение дискретного ряда распределения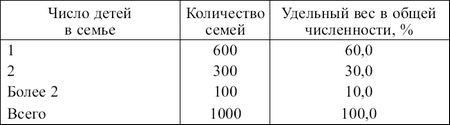

В случае непрерывной вариации величина признака может принимать любые значения в определенном интервале, например распределение работников фирмы по уровню дохода (табл. 3.6).

Таблица 3.6

Случай непрерывной вариации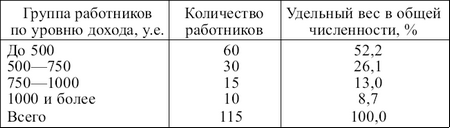

При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала. Оптимальное число групп выбирается так, чтобы отразить многообразие значений признака в совокупности. Чаще всего число групп устанавливается по формуле

k = 1 + 3,32lg N = 1,44ln N + 1,

где k – число групп; N – численность совокупности.

Например, необходимо построить вариационный ряд сельскохозяйственных предприятий по урожайности зерновых культур. Число сельскохозяйственных предприятий – 143. Как определить число групп?

k = 1 + 3,32lg N = 1 + 3,32lg143 = 8,16.

Число групп может быть только целым числом, в данном случае – 8 или 9.

Пример. Минимальная урожайность составляет 30 ц/га, максимальная – 70 ц/га, а число намеченных групп – 10. Величину интервала можно рассчитать по формуле (3.1):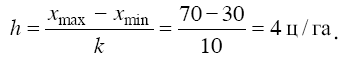

Если полученная группировка не удовлетворяет требованиям анализа, то можно произвести перегруппировку. Не следует стремиться к очень большому количеству групп, так как в такой группировке часто исчезают различия между группами. Также надо избегать образования и слишком малочисленных групп, включающих несколько единиц совокупности, потому что в таких группах перестает действовать закон больших чисел и возможно проявление случайности. Когда не удается сразу наметить возможные группы, собранный материал сначала разбивают на значительное количество групп, а затем укрупняют их, уменьшая количество групп и создавая качественно однородныле группыл.

Таким образом, группировки во всех случаях должны быть построены так, чтобы образованные в них группы как можно полнее отвечали действительности, были видны различия между группами и в одну группу не объединялись существенно различающиеся между собой явления.

После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать и анализировать без определенной, наглядной систематизации. Результаты статистических сводок и группировок получают оформление в виде статистических таблиц.

Статистическая таблица дает количественную характеристику статистической совокупности и представляет собой форму наглядного отображения полученных в результате статистической сводки и группировки числовых (цифровых) данных. По внешнему виду таблица представляет собой комбинацию вертикальных и горизонтальных строк. В ней обязательно должны быть общие боковые и верхние заголовки. Еще одной особенностью статистической таблицы является наличие подлежащего (характеристика статистической совокупности) и сказуемого (показатели, характеризующие совокупности). Статистические таблицы являются наиболее рациональной формой изложения результатов сводки или группировки.

Подлежащее таблицы представляет ту статистическую совокупность, о которой идет речь в таблице, т. е. перечень отдельных или всех единиц совокупности либо их групп. Чаще всего подлежащее помещается в левой части таблицы и содержит перечень строк. Сказуемое таблицы – это те показатели, с помощью которых дается характеристика явления, отображаемого в таблице. Подлежащее и сказуемое таблицы могут располагаться по-разному, главное, чтобы таблица была легко читаемой, компактной и легко воспринималась.

В статистической практике и исследовательских работах используются таблицы различной сложности. Это зависит от характера изучаемой совокупности, объема имеющейся информации, задач анализа. Если в подлежащем таблицы содержится простой перечень каких-либо объектов или территориальных единиц, таблица называется простой. В подлежащем простой таблицы нет каких-либо группировок статистических данных. Эти таблицы имеют самое широкое применение в статистической практике, например характеристика городов РФ по численности населения, средней зарплате и т. п. Если подлежащее простой таблицы содержит перечень территорий, например областей, краев, автономных округов, республик и т. д., то такая таблица называется территориальной. Простая таблица содержит только описательные сведения, ее аналитические возможности ограничены. Глубокий анализ исследуемой совокупности, взаимосвязей признаков предполагает построение более сложных таблиц – групповых и комбинационных.

Групповые таблицы в отличие от простых содержат в подлежащем не простой перечень единиц объекта наблюдения, а их группировку по одному существенному признаку. Простейшим видом групповой таблицы являются таблицы, в которых представлены ряды распределения (см. табл. 3.6). Групповая таблица может быть более сложной, если в сказуемом приводится не только число единиц в каждой группе, но и ряд других важных показателей, количественно и качественно характеризующих группы подлежащего. Такие таблицы часто используются в целях сопоставления обобщающих показателей по группам, что позволяет сделать определенные практические выводы. Более широкими аналитическими возможностями располагают комбинационные таблицы.

Комбинационными называются статистические таблицы, в подлежащем которых группы единиц, образованные по одному признаку, подразделяются на подгруппы по одному или нескольким признакам. В отличие от простых и групповых таблиц комбинационные позволяют проследить зависимость показателей сказуемого от нескольких признаков, которые легли в основу комбинационной группировки в подлежащем.

Наряду с перечисленными выше таблицами в статистической практике применяют таблицы сопряженности, или таблицы частот. В основе построения таких таблиц лежит группировка единиц совокупности по двум или более признакам, которые называются уровнями. Например, население делится по полу (мужской, женский) и т. п. Таким образом, признак А имеет n градаций (или уровней): A1, A2, An (в нашем примере n = 2). Далее изучается взаимодействие признака А с другим признаком – В, который подразделяется на m градаций (факторов): B1, B2, ..., Bm. В нашем примере признак В – принадлежность к какой-либо профессии, а B1, B2, Bm принимают конкретные значения (доктор, водитель, учитель, строитель и т. д.). Группировка по двум и более признакам используется для оценки взаимосвязей между признаками А и В.

Результаты наблюдений можно представить таблицей сопряженности, состоящей из n строк и m столбцов, в ячейках которых проставлены частоты событий nij, т. е. количество объектов выборки, обладающих комбинацией уровней Aj и Bj. Если между переменными A и B имеется взаимно-однозначная прямая или обратная функциональная связь, то все частоты nij концентрируются по одной из диагоналей таблицы. При не столь сильной связи некоторое число наблюдений попадает и на недиагональные элементы. В этих условиях перед исследователем стоит задача: выяснить, насколько точно можно предсказать значение одного признака по величине другого. Таблица частот называется одномерной, если в ней табулирована только одна переменная. Таблица, в основе которой лежит группировка по двум признакам (уровням), которые табулируются по двум признакам (факторам), называется таблицей с двумя входами. Таблицы частот, в которых табулируются значения двух или более признаков, называются таблицами сопряженности.

Из всех видов статистических таблиц наиболее широкое применение имеют простые таблицы, реже применяются групповые и особенно комбинационные статистические таблицы, а таблицы сопряженности строят для проведения специальных видов анализа. Статистические таблицы служат одним из важных способов выражения и изучения массовых общественных явлений, но лишь при условии правильного их построения.

Форма любой статистической таблицы должна наилучшим образом отвечать сущности выражаемого ею явления и целям его изучения. Это достигается путем соответствующей разработки подлежащего и сказуемого таблицы. Внешне таблица должна быть небольшой и компактной, иметь название, указание единиц измерения, а также времени и места, к которым относятся сведения. Заголовки строк и граф в таблице даются кратко, но четко. Чрезмерное загромождение таблицы цифровыми данными, неряшливое оформление затрудняют ее чтение и анализ. Перечислим основные правила построения статистических таблиц:

• таблица должна быть компактной и отражать только те исходные данные, которые прямо отражают исследуемое социально-экономическое явление в статике и динамике;

• заголовок таблицы, названия граф и строк должны быть четкими, краткими, лаконичными. В заголовке должны быть отражены объект, признак, время и место совершения события;

• графы и строки следует нумеровать;

• графы и строки должны содержать единицы измерения, для которых существуют общепринятые сокращения;

• информацию, сопоставляемую в ходе анализа, лучше всего располагать в соседних графах (либо одну под другой). Это облегчает процесс сравнения;

• для удобства чтения и работы числа в статистической таблице следует проставлять в середине граф, строго одно под другим: единицы – под единицами, запятая – под запятой;

• числа целесообразно округлять с одинаковой степенью точности (до целого знака, до десятой доли);

• отсутствие данных обозначается знаком умножения (х), если данная позиция не подлежит заполнению, отсутствие сведений обозначается многоточием (...), либо «н. д.», либо «н. св.», при отсутствии явления ставится знак тире (-);

• для отображения очень малых чисел используют обозначение 0.0 или 0.00;

• если число получено на основании условных расчетов, то его берут в скобки, сомнительные числа сопровождают вопросительным знаком, а предварительные – знаком (*).

В случае необходимости дополнительной информации статистические таблицы сопровождаются сносками и примечаниями, в которых разъясняются, например, сущность специфического показателя, примененной методологии и т. д. Сносками пользуются для того, чтобы указать на ограниченные обстоятельства, которые надо принять во внимание при чтении таблицы.

При соблюдении этих правил статистическая таблица становится основным средством представления, обработки и обобщения статистической информации о состоянии и развитии изучаемых социально-экономических явлений.

Полученные в результате сводки или статистического анализа в целом числовые показатели могут быть представлены не только в табличной, но и в графической форме. Использование графиков для представления статистической информации позволяет придать статистическим данным наглядность и выразительность, облегчить их восприятие, а во многих случаях и анализ. Многообразие графических представлений статистических показателей дает огромные возможности для наиболее выразительной демонстрации явления или процесса.

Графиками в статистике называются условные изображения числовых величин и их соотношений в виде различных геометрических образов: точек, линий, плоских фигур и т. п. Статистический график позволяет сразу оценить характер изучаемого явления, присущие ему закономерности и особенности, тенденции развития, взаимосвязь характеризующих его показателей.

Каждый график состоит из графического образа и вспомогательных элементов. Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Вспомогательные элементы графика включают общее название графика, оси координат, шкалы, числовые сетки и числовые данные, дополняющие и уточняющие изображаемые показатели. Вспомогательные элементы облегчают чтение графика и его истолкование.

Название графика должно кратко и точно раскрывать его содержание. Пояснительные тексты могут располагаться в пределах графического образа или рядом с ним либо выноситься за его пределы.

Оси координат с нанесенными на них шкалами и числовые сетки необходимы для построения графика и пользования им. Шкалы могут быть прямолинейными или криволинейными (круговыми), равномерными (линейными) и неравномерными. Иногда целесообразно применять так называемые сопряженные шкалы, построенные на одной или двух параллельных линиях. Чаще всего одна из сопряженных шкал используется для отсчета абсолютных величин, а вторая – соответствующих им относительных. Числа на шкалах проставляются равномерно, при этом последнее число должно превышать максимальный уровень показателя, значение которого отсчитывается по этой шкале. Числовая сетка, как правило, должна иметь базовую линию, роль которой обычно играет ось абсцисс.

Статистические графики можно классифицировать по разным признакам: назначению (содержанию), способу построения и характеру графического образа.

По содержанию, или назначению, можно выделить:

графики сравнения в пространстве;

графики различных относительных величин (структуры, динамики и др.);

графики вариационных рядов;

графики размещения по территории;

графики взаимосвязанных показателей и т. д.

По способу построения графики можно разделить на диаграммы и статистические карты. Диаграммы – наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку. Статистические карты – графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь потому, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных.

По характеру графического образа различают графики точечные, линейные, плоскостные (столбиковые, полосовые, квадратные, круговые, секторные, фигурные) и объемные. При построении точечных диаграмм в качестве графических образов применяются совокупности точек, при построении линейных – линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур. Статистические карты по графическому образу делятся на картограммы и картодиаграммы .

В зависимости от круга решаемых задач выделяются диаграммы сравнения, структурные диаграммы и диаграммы динамики. Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы, принцип построения которых состоит в изображении статистических показателей в виде поставленных по вертикали прямоугольников – столбиков. Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравниваемые показатели выражены в одной единице измерения. При построении столбиковых диаграмм необходимо начертить систему пря-

моугольных координат, в которой располагаются столбики. На горизонтальной оси располагаются основания столбиков, величина основания определяется произвольно, но устанавливается одинаковой для всех. Шкала, определяющая масштаб столбиков по высоте, расположена по вертикальной оси. Величина каждого столбика по вертикали соответствует размеру изображаемого на графике статистического показателя. Таким образом, у всех столбиков, составляющих диаграмму, переменной величиной является только одно измерение. Размещение столбиков в поле графика может быть различным:

на одинаковом расстоянии друг от друга;

вплотную друг к другу;

в частичном наложении друг на друга.

Правила построения столбиковых диаграмм допускают одновременное расположение на одной горизонтальной оси изображений нескольких показателей. В этом случае столбики располагаются группами, для каждой из которых может быть принята разная размерность варьирующих признаков.

Разновидности столбиковых диаграмм составляют так называемые ленточные и полосовые диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху и определяет величину полос по длине. Область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения. Одномерность изображаемых статистических показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков – по высоте, полос – по длине) и пропорциональности изображаемым величинам. Для выполнения этого требования необходимо, во-первых, чтобы шкала, по которой устанавливается размер столбика (полосы), начиналась с нуля; во-вторых, эта шкала должна быть непрерывной, т. е. охватывать все числа данного статистического ряда; разрыв шкалы и соответственно столбиков (полос) не допускается. Невыполнение указанных правил приводит к искаженному графическому представлению анализируемого статистического материала. Столбиковые и полосовые диаграммы как прием графического изображения статистических данных взаимозаменяемы, т. е. рассматриваемые статистические показатели равно могут быть представлены как столбиками, так и полосами. И в том и в другом случае для изображения величины явления используется одно измерение каждого прямоугольника – высота столбика или длина полосы, поэтому и сфера применения этих двух диаграмм в основном одинакова.

Разновидностью столбиковых и ленточных диаграмм являются направленные диаграммы. Они отличаются от обычных двусторонним расположением столбиков или полос и имеют начало отсчета по масштабу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков или полос, направленных в разные стороны, менее эффективно, чем расположенных рядом в одном направлении. Несмотря на это, анализ направленных диаграмм позволяет делать достаточно содержательные выводы, так как особое расположение придает графику яркое изображение. К группе двусторонних относятся диаграммыг чис-тыгх отклонений. В них полосы направлены в обе стороны от вертикальной нулевой линии: вправо – для прироста, влево – для уменьшения. С помощью таких диаграмм удобно изображать отклонения от плана или некоторого уровня, принятого за базу сравнения. Важным достоинством рассматриваемых диаграмм является возможность видеть размах колебаний изучаемого статистического признака, что само по себе имеет большое значение для анализа.

Для простого сравнения не зависимых друг от друга показателей могут также использоваться диаграммы, принцип построения которых состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы их площади соответствовали тому количеству, которые эти фигуры отображают. Другими словами, эти диаграммы выражают величину изображаемого явления размером своей площади. Для получения диаграмм рассматриваемого типа используют разнообразные геометрические фигуры: квадрат, круг, реже прямоугольник. Известно, что площадь квадрата равна квадрату его стороны, а площадь круга определяется пропорционально квадрату его радиуса, поэтому для построения диаграмм необходимо сначала из сравниваемых величин извлечь квадратный корень. Затем на базе полученных результатов нужно определить сторону квадрата или радиус круга соответственно принятому масштабу.

Наиболее выразительным и легко воспринимаемым является способ построения диаграмм сравнения в виде фигур-знаков. В этом случае статистические совокупности изображаются не геометрическими фигурами, а символами, или знаками, воспроизводящими в какой-то степени внешний образ статистических данных. Достоинство такого способа графического изображения заключается в высокой степени наглядности, в получении подобного отображения, отражающего содержание сравниваемых совокупностей.

Важнейший признак любой диаграммы – масштаб, поэтому, чтобы правильно построить фигурную диаграмму, необходимо определить единицу счета. В качестве последней принимается отдельная фигура (символ), которой условно присваивается конкретное численное значение. А исследуемая статистическая величина изображается отдельным количеством одинаковых по размеру фигур, последовательно располагающихся на рисунке. Однако в большинстве случаев не удается изобразить статистический показатель целым количеством фигур. Последнюю из них приходится делить на части, так как по масштабу один знак является слишком крупной единицей измерения. Обычно эта часть определяется на глаз. Сложность точного ее определения является недостатком фигурных диаграмм. Однако большая точность представления статистических данных не преследуется, и результаты получаются вполне удовлетворительными. Как правило, фигурные диаграммы широко используются для популяризации статистических данных и рекламы.

Основное строение структурных диаграмм заключается в графическом представлении состава статистических совокупностей, характеризующихся как соотношение различных частей каждой из совокупностей. Состав статистической совокупности графически может быть представлен с помощью как абсолютных, так и относительных показателей.

В первом случае не только размеры частей, но и размер графика в целом определяются статистическими величинами и изменяются в соответствии с изменениями последних. Во втором – размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100 %), а меняются только размеры отдельных его частей. Графическое изображение состава совокупности по абсолютным и относительным показателям способствует проведению более глубокого анализа и позволяет проводить международные сопоставления и сравнения социально-экономических явлений.

Наиболее распространенным способом графического изображения структуры статистических совокупностей является секторная диаграмма, которая считается основной формой диаграммы такого назначения. Это объясняется тем, что идея целого хорошо и наглядно выражается кругом, который отображает всю совокупность. Удельный вес каждой части совокупности в секторной диаграмме характеризуется величиной центрального угла (угол между радиусами круга). Сумма всех углов круга, равная 360°, приравнивается к 100 %, а следовательно, 1 % принимается равным 3,6°. Применение секторных диаграмм позволяет не только графически изобразить структуру совокупности и ее изменение, но и показать динамику численности этой совокупности. Для этого строятся круги, пропорциональные объему изучаемого признака, а затем секторами выделяются его отдельные части. Рассмотренный способ графического изображения структуры совокупности имеет как достоинства, так и недостатки. Так, секторная диаграмма сохраняет наглядность и выразительность лишь при небольшом числе частей совокупности, в противном случае ее применение малоэффективно. Кроме того, наглядность секторной диаграммы снижается при незначительных изменениях структуры изображаемых совокупностей: она выше, если существеннее различия сравниваемых структур.

Преимуществом столбиковых и ленточных структурных диаграмм по сравнению с секторными являются их большая емкость, возможность отразить более широкий объем полезной информации. Однако эти диаграммы более эффективны при малых различиях в структуре изучаемой совокупности.

Для изображения и вынесения суждений о развитии явления во времени строятся диаграммы динамики. Для наглядного изображения явлений в рядах динамики используются диаграммы столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграмм зависит в основном от особенностей исходных данных, цели исследования. Например, если имеется ряд динамики с несколькими неравноотстоящими уровнями во времени (1914, 1949, 1980, 1985, 1996, 2003 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не пригодны для отображения большого числа уровней, так как громоздки.

Когда число уровней в ряду динамики велико, целесообразно применять линейныге диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать, если:

• целью исследования является изображение общей тенденции и характера развития явления;

• на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения;

• наиболее существенным является сопоставление темпов роста, а не уровней.

Для построения линейных графиков применяют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д.), а по оси ординат – размеры изображаемых явлений или процессов. На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. В данном графике необходимо соблюдать равновесие, пропорциональность между осями координат, так как нарушение равновесия между осями координат дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, увеличение масштаба по оси ординат по сравнению с масштабами на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.

В статистической практике чаще всего применяются графические изображения с равномерными шкалами. По оси абсцисс они берутся пропорционально числу периодов времени, а по оси ординат – пропорционально самим уровням. Масштабом равномерной шкалы будет длина отрезка, принятого за единицу. Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя. Однако на одном графике не следует помещать более трех-четырех кривых, так как большое их количество неизбежно осложняет чертеж и линейная диаграмма теряет наглядность. В некоторых случаях нанесение на один график двух кривых дает возможность одновременно изобразить динамику третьего показателя, если он является разностью первых двух. Например, при изображении динамики рождаемости и смертности площадь между двумя кривыми показывает величину естественного прироста или естественной убыли населения.

Иногда необходимо сравнить на графике динамику двух показателей, имеющих различные единицы измерения. В таких случаях понадобится не одна, а две масштабные шкалы. Одну из них размещают справа, другую – слева. Однако такое сравнение кривых не дает достаточно полной картины динамики этих показателей, так как масштабы произвольны, поэтому сравнение динамики уровня двух разнородных показателей следует осуществлять на основе использования одного масштаба после преобразования абсолютных величин в относительные.

Линейные диаграммы с линейной шкалой имеют один недостаток, снижающий их познавательную ценность: равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения. Именно относительные изменения экономических показателей динамики искажаются при их изображении на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени. В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему.

Основная идея полулогарифмической системы! состоит в том, что в ней равным линейным отрезкам соответствуют равные значения логарифмов чисел. Такой подход имеет преимущество: возможность уменьшения размеров больших чисел через их логарифмический эквивалент. Однако с масштабной шкалой в виде логарифмов график малодоступен для понимания. Необходимо рядом с логарифмами, обозначенными на масштабной шкале, проставить сами числа, характеризующие уровни изображаемого ряда динамики, которые соответствуют указанным числам логарифмов. Такого рода графики носят название графиков на полулогарифмической сетке. Полулогарифмической сеткой называется сетка, в которой на одной оси нанесен линейный масштаб, а на другой – логарифмический.

Динамику изображают и радиальныге диаграммыг, строящиеся в полярных координатах. Радиальные диаграммы преследуют цель наглядного изображения определенного ритмического движения во времени. Чаще всего эти диаграммы применяются для иллюстрации сезонных колебаний. Радиальные диаграммы разделяются на замкнутые и спиральные. По технике построения радиальные диаграммы отличаются друг от друга в зависимости от того, что взято в качестве пункта отсчета – центр круга или окружность. Замкнутыге диаграммыг отражают внутригодичный цикл динамики какого-либо одного года. Спиральныге диаграммы! показывают внутригодичный цикл динамики за ряд лет. Построение замкнутых диаграмм сводится к следующему: вычерчивается круг, среднемесячный показатель приравнивается к радиусу этого круга. Затем весь круг делится на 12 частей, равных радиусу, которые на графике приводятся в виде тонких линий. Каждый радиус обозначает месяц, причем расположение месяцев аналогично циферблату часов: январь – в том месте, где на часах 1, февраль – где 2 и т. д. На каждом радиусе делается отметка в определенном месте согласно масштабу исходя из данных за соответствующий месяц. Если данные превышают среднегодовой уровень, отметка делается за пределами окружности на продолжении радиуса. Затем отметки различных месяцев соединяются отрезками.

Если же в качестве базы для отчета взят не центр круга, а окружность, то такие диаграммы называются спиральными. Построение спиральных диаграмм отличается от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь ряд динамики в виде спирали. Особенно наглядна такая диаграмма, когда наряду с сезонными изменениями происходит неуклонный рост из года в год.

Статистические карты1 представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории. Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.

Картограммы – это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской определенной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределения районов по урожайности зерновых культур и т. п.). Картограммы делятся на фоновые и точечные. Картограмма фоновая – вид картограммы, на которой штриховкой различной густоты или окраской определенной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы. Картограмма точечная – вид картограммы, где уровень выбранного явления изображается с помощью точек. Точка изображает одну единицу в совокупности или некоторое их количество, показывая на географической карте плотность или частоту проявления определенного признака.

Фоновые картограммы, как правило, используются для изображения средних или относительных показателей, точечные – для объемных (количественных) показателей (численность населения, поголовье скота и т. д.).

Вторую большую группу статистических карт составляют картодиаграммы, представляющие собой сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы. Среди картодиаграмм следует выделить картодиаграммы простого сравнения, графики пространственного перемещения, изолинии.

На картодиаграмме простого сравнения в отличие от обычной диаграммы диаграммные фигуры, изображающие величины исследуемого показателя, расположены не в ряд, как на обычной диаграмме, а разносятся по всей карте в соответствии с тем районом, областью или страной, которые они представляют. Элементы простейшей картодиаграммы можно обнаружить на политической карте, где города отличаются различными геометрическими фигурами в зависимости от числа жителей.

Изолинии – это линии равного значения какой-либо величины в ее распространении на поверхности, в частности на географической карте или графике. Изолиния отражает непрерывное изменение исследуемой величины в зависимости от двух других переменных и применяется при картографировании природных и социально-экономических явлений. Изолинии используются для получения количественных характеристик исследуемых величин и для анализа корреляционных связей между ними.

Природа и содержание статистических показателей соответствует тем экономическим и социальным явлениям и процессам, которые их отражают. Все экономические и социальные категории или понятия носят абстрактный характер, отражают наиболее существенные черты, общие взаимосвязи явлений. И для того чтобы измерить размеры и соотношения явлений или процессов, т. е. дать им соответствующую количественную характеристику, разрабатывают экономические и социальные показатели, соответствующие каждой категории (понятию). Именно соответствием показателей сущности экономических категорий обеспечивается единство количественной и качественной характеристик экономических и социальных явлений и процессов.

Различают два вида показателей экономического и социального развития общества: плановые (прогнозные) и отчетные (статистические). Плановые показатели представляют собой определенные конкретные значения показателей, достижение которых прогнозируется в будущих периодах. Отчетные показатели (статистические) характеризуют реально сложившиеся условия экономического и социального развития, фактически достигнутый уровень за определенный период; это объективная количественная характеристика (мера) общественного явления или процесса в его качественной определенности в конкретных условиях места и времени. Каждый статистический показатель имеет качественное социально-экономическое содержание и связанную с ним методологию измерения. Статистический показатель имеет также ту или иную статистическую форму (структуру) и может выражать:

• общее число единиц совокупности;

• общую сумму значений количественного признака этих единиц;

• среднюю величину признака;

• величину данного признака по отношению к величине другого и т. п.

Статистический показатель имеет также определенное количественное значение. Это численное значение статистического показателя, выраженное в определенных единицах измерения, называется величиной показателя.

Величина показателя обычно варьируется в пространстве и колеблется во времени. Поэтому обязательным атрибутом статистического показателя являются также указание территории и момента либо периода времени.

Статистические показатели можно условно подразделить на первичные (объемные, количественные, экстенсивные) и вторичные (производные, качественные, интенсивные).

Первичные показатели характеризуют либо общее число единиц совокупности, либо сумму значений какого-либо их признака. Взятые в динамике, в изменении во времени, они характеризуют экстенсивный путь развития экономики в целом или конкретного предприятия в частном случае. По статистической форме эти показатели являются суммарными статистическими величинами.

Вторичныге показатели обычно выражаются средними и относительными величинами и, взятые в динамике, обычно характеризуют путь интенсивного развития.

Показатели, характеризующие размер сложного комплекса социально-экономических явлений и процессов, часто называют синтетическими (валовый внутренний продукт (ВВП), национальный доход, производительность общественного труда, потребительская корзина и др.).

В зависимости от применяемый единиц измерения различают показатели натуральные, стоимостные и трудовые (в человеко-часах, нормо-часах). В зависимости от сферыг

применения различают показатели, исчисленные на региональном, отраслевом уровнях и т. д. По точности отражаемого явления различают ожидаемые, предварительные и окончательные величины показателей.

В зависимости от объема и содержания объекта статистического изучения различают индивидуальные (характеризующие отдельные единицы совокупности) и сводные (обобщающие) показатели. Таким образом, статистические величины, которые характеризуют собой массы или совокупности единиц, называются обобщающими статистическими показателями (величинами). Обобщающие показатели играют очень важную роль в статистическом исследовании благодаря следующим отличительным особенностям:

дают сводную (концентрированную) характеристику совокупностям единиц изучаемых общественных явлений;

выражают существующие между явлениями связи, зависимости и обеспечивают, таким образом, взаимосвязанное изучение явлений;

характеризуют происходящие в явлениях изменения, складывающиеся закономерности их развития и пр., т. е. выполняют экономико-статистический анализ рассматриваемых явлений, в том числе и на основе разложения самих обобщающих величин на составляющие их части, определяющие их факторы и т. п.

Объективное и достоверное исследование сложных экономических и социальных категорий возможно только на основе системы статистических показателей, которые в единстве и взаимосвязи характеризуют различные стороны и аспекты состояния и динамики развития этих категорий.

Статистические показатели, объективно отражая единство и взаимосвязи экономических и социальных явлений и процессов, не являются надуманными, произвольно сконструированными догмами, установленными раз и навсегда. Наоборот, динамичное развитие общества, науки, вычислительной техники, совершенствование статистической методологии приводят к тому, что устаревшие, потерявшие свое значение показатели изменяются либо исчезают и появляются новые, более совершенные показатели, объективно и достоверно отражающие современные условия общественного развития.

Таким образом, построение и совершенствование статистических показателей должно основываться на соблюдении двух основных принципов:

• объективности и реальности (показатели должны правдиво и адекватно отражать сущность соответствующих экономических и социальных категорий (понятий));

• всесторонней теоретической и методологической обоснованности (определение величины показателя, его измеримость и сопоставимость в динамике должны быть научно аргументированы, четко и доступно сформулированы и однозначно, в единообразном толковании применимы).

Кроме того, величины показателей должны правильно количественно измеряться с учетом уровня, масштабов и качественных признаков состояния или развития соответствующего экономического или социального явления (отраслевой и региональной уровни, отдельное предприятие или работник и т. п.). При этом построение показателей должно носить сквозной характер, позволяющий не только суммировать соответствующие показатели, но и обеспечивать их качественную однородность в группах и совокупностях, переход от одного показателя к другому для полной характеристики объема и структуры более сложной категории или явления. Наконец, построение статистического показателя, его структура и сущность должны предусматривать возможность всесторонне анализировать изучаемое явление или процесс, характеризовать особенности его развития, определять влияющие на него факторы.

Вычисление статистических величин и анализ данных об изучаемых явлениях – это третий и завершающий этап статистического исследования. В статистике рассматривают несколько видов статистических величин: абсолютные, относительные и средние величины. К числу обобщающих статистических показателей относятся также аналитические показатели рядов динамики, индексы и др.

Статистическое наблюдение независимо от его масштабов и целей всегда дает информацию о тех или иных социально-экономических явлениях и процессах в виде абсо-лютны1х показателей, т. е. показателей, представляющих собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Качественная определенность абсолютных показателей заключается в том, что они напрямую связаны с конкретным содержанием изучаемого явления или процесса, с его сущностью. В связи с этим абсолютные показатели и абсолютные величины должны иметь определенные единицы измерения, которые наиболее полно и точно отражали бы его сущность (содержание).

Абсолютные показатели являются количественным выражением признаков статистических явлений. Например, рост – это признак, а его значение – это показатель роста.

Абсолютный показатель должен характеризовать размер изучаемого явления или процесса в данном месте и в данное время, он должен быть «привязан» к какому-нибудь объекту или территории и может характеризовать либо отдельную единицу совокупности (отдельный объект) – предприятие, рабочего, либо группу единиц, представляющую часть статистической совокупности, или статистическую совокупность в целом, например численность населения в стране, и т. п. В первом случае речь идет об индивидуальных абсолютных показателях, а во втором – о сводных абсолютных показателях.

Индивидуальными называют абсолютные величины, характеризующие размеры отдельных единиц совокупности (например, количество деталей, изготовленных одним рабочим за смену, число детей в отдельной семье). Их получают непосредственно в процессе статистического наблюдения и фиксируют в первичных учетных документах. Индивидуальные показатели получают в процессе статистического наблюдения за теми или иными явлениями и процессами как результат оценки, подсчета, замера фиксированного интересующего количественного признака.

Сводные абсолютные величины получаются, как правило, путем суммирования отдельных индивидуальных величин. Сводные абсолютные показатели получают в результате сводки и группировки значений индивидуальных абсолютных показателей. Так, например, в процессе переписи населения органы государственной статистики получают итоговые абсолютные данные о численности населения страны, о распределении его по регионам, по полу, возрасту и т. д.

К абсолютным показателям также можно отнести показатели, которые получаются не в результате статистического наблюдения, а в результате какого-либо расчета. Как правило, данные показатели – это разность между двумя абсолютными показателями. Например, естественный прирост (убыль) населения находится как разность между числом родившихся и числом умерших за определенный период времени; прирост продукции за год находится как разность между объемом произведенной продукции на конец года и объемом произведенной продукции на начало года. При составлении долгосрочных прогнозов развития экономики страны рассчитывают предположительные данные о материальных, трудовых, финансовых ресурсах. Как видно из примеров, эти показатели будут абсолютными, так как имеют абсолютные единицы измерения.

Абсолютные величины отражают естественную основу явлений, т. е. выражают либо численность единиц изучаемой совокупности, ее отдельных составных частей, либо их абсолютные размеры в натуральных единицах, вытекающих из их физических свойств (вес, длина и т. п.), или в единицах измерения, вытекающих из их экономических свойств (стоимость, затраты труда). Следовательно, абсолютные величины всегда имеют определенную размерность.

Кроме того, абсолютные статистические показатели всегда выражаются в натуральных, стоимостных и трудовых единицах измерения в зависимости от сущности описываемых ими процессов и явлений.

Натуральные измерители характеризуют явления в свойственной им натуральной форме и выражаются в мерах длины, веса, объема и т. п. или количеством единиц, числом событий. К натуральным можно отнести такие единицы измерения, как тонна, килограмм, метр и т. д., например: объем жилищного строительства составил 2000 м2.

В ряде случаев используются комбинированные единицы измерения, представляющие собой произведение двух величин, выраженных в различных размерностях. Так, например, производство электроэнергии измеряется в киловатт-часах, грузооборот – в тонна-километрах и т. п.

В группу натуральных единиц измерения входят и так называемые условно натуральныге единицы измерения. Их применяют для получения суммарных абсолютных вели-

чин в случае, когда индивидуальные величины характеризуют отдельные разновидности продукции, близкие по своим потребительским свойствам, но отличающиеся, например, содержанием жира, спирта, калорийностью и т. п. При этом одна из разновидностей продукции принимается за условный натуральный измеритель, и к ней с помощью переводных коэффициентов, выражающих соотношение потребительских свойств (иногда трудоемкости, себестоимости и т. д.) отдельных разновидностей, приводятся все разновидности этого продукта.

Трудовые единицы измерения используют для характеристики показателей, которые позволяют оценить затраты труда, отражают наличие, распределение и использование трудовых ресурсов, например трудоемкость выполненных работ в человеко-днях.

Натуральные, а иногда и трудовые измерители не позволяют получить сводные абсолютные показатели в условиях разнородной продукции. В этом плане универсальными являются стоимостные единицы измерения, которые дают стоимостную (денежную) оценку социально-экономическим явлениям, характеризуют стоимость определенной продукции или объема выполненных работ. Например, в денежной форме выражаются такие важные для экономики страны показатели, как национальный доход, валовой внутренний продукт, а на уровне предприятия – прибыль, собственные и заемные средства.

Наибольшее предпочтение в статистике отдается стоимостным единицам измерения, так как стоимостный учет является универсальным, однако он не всегда может быть приемлем.

Абсолютные показатели могут быть рассчитаны во времени и пространстве. Например, динамика численности населения Российской Федерации с 1991 по 2004 г. отражается временным фактором, а уровень цен на хлебобулочные изделия по регионам РФ за 2004 г. характеризуется пространственным сравнением.

При учете абсолютных показателей во времени (в динамике) их регистрация может быть осуществлена на определенную дату, т. е. какой-либо момент времени (стоимость основных средств предприятия на начало года) и за какой-либо период времени (число родившихся за год). В первом случае показатели являются моментальными, во втором – интервальными.

С точки зрения пространственной определенности абсолютные показатели делят следующим образом: общие территориальные, региональные и локальные. Например, объем ВВП (валовой внутренний продукт) – общий территориальный показатель, объем ВРП (валовой региональный продукт) – региональный признак, численность занятых в городе – локальный признак, т. е. первая группа показателей характеризует страну в целом, региональные – конкретный регион, локальные – отдельный город, населенный пункт и т. д.

Абсолютные показатели не дают ответа на вопрос, какую долю имеет та или иная часть в общей совокупности, не могут охарактеризовать уровни планового задания, степень выполнения плана, интенсивность того или иного явления, так как они не всегда пригодны для сравнения и поэтому часто используются лишь для расчета относительных величин.

Наряду с абсолютными величинами одной из важнейших форм обобщающих показателей в статистике являются относительные величины – это обобщающие показатели, выражающие меру количественных соотношений, присущих конкретным явлениям или статистическим объектам. При расчете относительной величины измеряется отношение двух взаимосвязанных величин (преимущественно абсолютных), что очень важно в статистическом анализе. Относительные величины широко используются в статистическом исследовании, так как они позволяют провести сравнения различных показателей и делают такое сравнение наглядным.

Относительные величины вычисляются как отношение двух чисел. При этом числитель называется сравниваемой величиной, а знаменатель – базой относительного сравнения. В зависимости от характера изучаемого явления и задач исследования базисная величина может принимать различные значения, что приводит к различным формам выражения относительных величин. Относительные величины измеряются:

• в коэффициентах: если база сравнения принята за 1, то относительная величина выражается целым или дробным числом, показывающим, во сколько раз одна величина больше другой или какую часть ее составляет;

• в процентах, если база сравнения принимается за 100;

• в промилле, если база сравнения принимается за 1000;

• в продецимилле, если база сравнения принимается за 10 000;

• в именованных числах (км, кг, га) и др.

В каждом конкретном случае выбор той или иной формы относительной величины определяется задачами исследования и социально-экономической сущностью, мерой которого выступает искомый относительный показатель. По своему содержанию относительные величины подразделяются на следующие виды:

• выполнения договорных обязательств;

• динамики;

• структуры;

• координации;

• интенсивности;

• сравнения.

Относительная величина договорных обязательств представляет собой отношение фактического выполнения договора к уровню, предусмотренному договором:

Эта величина отражает степень выполнения предприятием своих договорных обязательств, и может быть выражена в виде числа (целого или дробного) или в процентах. При этом необходимо, чтобы числитель и знаменатель исходного отношения соответствовали одному и тому же договорному обязательству.

Относительными величинами динамики – темпами роста – называются показатели, характеризующие изменение величины общественных явлений во времени. Относительная величина динамики показывает изменение однотипных явлений за период времени. Рассчитывается эта величина посредством сравнения каждого последующего

периода с первоначальным или предыдущим. В первом случае получаем базисные величины динамики, а во втором – цепные величины динамики. И те и другие величины выражаются либо в коэффициентах, либо в процентах. Выбору базы сравнения при расчете относительных величин динамики, как и других относительных показателей, следует уделять особое внимание, так как от этого в существенной мере зависит практическая ценность полученного результата.

Относительные величиныг структуры^ характеризуют составные части изучаемой совокупности. Относительная величина совокупности рассчитывается по формуле

Относительные величины структуры, обычно называемые удельными весами, рассчитываются делением определенной части целого на общий итог, принимаемый за 100 %. У этой величины есть одна особенность – сумма относительных величин изучаемой совокупности всегда равна 100 % или 1 (в зависимости от того, в чем она выражается). Относительные величины структуры применяются при изучении сложных явлений, распадающихся на ряд групп или частей, для характеристики удельного веса (доли) каждой группы в общем итоге.

Относительные величины координации характеризуют соотношение отдельных частей совокупности с одной из них, принятой за базу сравнения. При определении этой величины одна из частей целого берется за базу для сравнения. С помощью этой величины можно соблюдать пропорции между составляющими совокупности. Показателями координации является, например, число городских жителей, приходящихся на 100 сельских; число женщин, приходящихся на 100 мужчин, и т. п. Характеризуя соотношение между отдельными частями целого, относительные величины координации придают им наглядность и позволяют, если это возможно, контролировать соблюдение оптимальных пропорций. Так как числитель и знаменатель относительных величин координации имеют одинаковую единицу измерения, то эти величины выражаются не в именованных числах, а в процентах, промилле или кратных отношениях.

Относительными величинами интенсивности называются показатели, определяющие степень распространенности данного явления в какой-либо среде. Они рассчитываются как отношение абсолютной величины данного явления к размеру среды, в которой оно развивается. Относительные величины интенсивности находят широкое применение в практике статистики. Примером этой величины может быть отношение численности населения к площади, на которой оно проживает, фондоотдача, обеспеченность населения врачебной помощью (численность врачей на 10 000 населения), уровень производительности труда (выпуск продукции на одного работника или в единицу рабочего времени) и т. п.

Таким образом, относительные величины интенсивности характеризуют эффективность использования различного рода ресурсов (материальных, финансовых, трудовых), социальный и культурный уровень жизни населения страны, многие другие аспекты общественной жизни.

Относительные величины интенсивности вычисляются путем сопоставления разноименных абсолютных величин, находящихся в определенной связи друг с другом, и в отличие от других видов относительных величин являются обычно именованными числами и имеют размерность тех абсолютных величин, соотношение которых они выражают. Тем не менее в ряде случаев, когда полученные результаты расчетов слишком малы, их умножают для наглядности на 1000 или 10 000, получая характеристики в промилле и продецимилле.

Особый интерес представляет разновидность относительных величин интенсивности – валовой внутренний продукт на душу населения. Применяя этот показатель в различных отраслях или конкретных видах продукции, можно получать следующие относительные величины интенсивности: производство электроэнергии, топлива, машин, оборудования, услуг, товаров и т. д. на душу населения.

Относительными величинами сравнения называются относительные показатели, получающиеся в результате сравнения одноименных уровней, относящихся к различным объектам или территориям, взятым за один и тот же период или на один момент времени. Они также исчисляются в коэффициентах или процентах и показывают, во сколько раз одна сравнимая величина больше или меньше другой.

Относительные величины сравнения находят широкое применение при сравнительной оценке различных показателей работы отдельных предприятий, городов, регионов, стран. При этом, например, результаты работы конкретного предприятия и т. п. принимаются за базу сравнения и последовательно соотносятся с результатами аналогичных предприятий других отраслей, регионов, стран и т. д.

В статистическом изучении общественных явлений абсолютные и относительные величины дополняют друг друга. Если абсолютные величины характеризуют как бы статику явлений, то относительные величины позволяют изучить степень, динамику, интенсивность развития явлений. Для правильного применения и использования абсолютных и относительных величин в экономико-статистическом анализе необходимо:

• учитывать специфику явлений при выборе и расчете того или иного вида абсолютных и относительных величин (поскольку количественная сторона явлений, характеризуемая этими величинами, неразрывно связана с их качественной стороной);

• обеспечить сопоставимость сравниваемой и базисной абсолютной величины с точки зрения объема и состава представляемых ими явлений, правильности методов получения самих абсолютных величин;

• комплексно использовать в процессе анализа относительные и абсолютные величины и не отрывать их друг от друга (так как использование одних только относительных величин в отрыве от абсолютных может привести к неточным и даже ошибочным выводам).

Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака. Для выяснения сущности средней величины необходимо рассмотреть особенности формирования значений признаков тех явлений, по данным которых исчисляют среднюю величину.

Известно, что единицы каждого массового явления обладают многочисленными признаками. Какой бы из этих признаков мы ни взяли, его значения у отдельных единиц будут различными, они изменяются, или, как говорят в статистике, варьируют от одной единицы к другой. Так, например, заработная плата работника определяется его квалификацией, характером труда, стажем работы и целым рядом других факторов, поэтому изменяется в весьма широких пределах. Совокупное влияние всех факторов определяет размер заработка каждого работника, тем не менее можно говорить о среднемесячной заработной плате работников разных отраслей экономики. Здесь мы оперируем типичным, характерным значением варьирующего признака, отнесенным к единице многочисленной совокупности.

Средняя величина отражает то общее, что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень (или размер) любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное для всех единиц изучаемой совокупности, которое и отражается в средней величине. Другие являются индивидуальными, их действие выражено слабее и носит эпизодический, случайный характер. Они действуют в обратном направлении, обусловливают различия между количественными признаками отдельных единиц совокупности, стремясь изменить постоянную величину изучаемых признаков. Действие индивидуальных признаков погашается в средней величине. В совокупном влиянии типичных и индивидуальных факторов, которое уравновешивается и взаимно погашается в обобщающих характеристиках, проявляется в общем виде известный из математической статистики фундаментальный закон больших чисел.

В совокупности индивидуальные значения признаков сливаются в общую массу и как бы растворяются. Отсюда и средняя величина выступает как «обезличенная», которая может отклоняться от индивидуальных значений признаков, не совпадая количественно ни с одним из них. Средняя величина отражает общее, характерное и типичное для всей совокупности благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц, так как ее величина определяется как бы общей равнодействующей из всех причин.

Однако для того, чтобы средняя величина отражала наиболее типичное значение признака, она должна определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений. Следовательно, средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.

Определяя, таким образом, сущность средних величин, необходимо подчеркнуть, что правильное исчисление любой средней величины предполагает выполнение следующих требований:

• качественная однородность совокупности, по которой вычислена средняя величина. Это означает, что исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;

• исключение влияния на вычисление средней величины случайных, сугубо индивидуальных причин и факторов. Это достигается в том случае, когда вычисление средней основывается на достаточно массовом материале, в котором проявляется действие закона больших чисел, и все случайности взаимно погашаются;

• при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показа-телъ (свойство), на который она должна быть ориентирована. Определяющий показатель может выступать в виде суммы значений осредняемого признака, суммы его обратных значений, произведения его значений и т. п. Связь между определяющим показателем и средней величиной выражается в следующем: если все значения осредняемого признака заменить средним значением, то их сумма или произведение в этом случае не изменит определяющего показателя. На основе этой связи определяющего показателя со средней величиной строят исходное количественное отношение для непосредственного расчета средней величины. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.

Средняя величина, рассчитанная в целом по совокупности, называется общей средней; средние величины, рассчитанные для каждой группы, – групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику явления, складывающуюся в конкретных условиях данной группы.

Способы расчета могут быть разные, поэтому в статистике различают несколько видов средней величины, основными из которых являются средняя арифметическая, средняя гармоническая и средняя геометрическая.

В экономическом анализе использование средних величин является основным инструментом для оценки результатов научно-технического прогресса, социальных мероприятий, поиска резервов развития экономики. В то же время следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.

В статистике используют различные виды средних величин, которые делятся на два больших класса:

• степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадра-тическая, средняя кубическая);

• структурные средние (мода, медиана).

Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Мода и медиана определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.

Самый распространенный вид средней величины – средняя арифметическая. Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7, третий – 4, четвертый – 10, пятый– 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для опреде-

ления средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна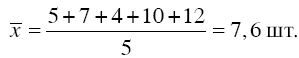

Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную. Например, рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где xi – варианты осредняемого признака, fi – частота, которая показывает, сколько раз встречается i-е значение в совокупности (табл. 5.1).

Таблица 5.1

Средний возраст студентов

Применяя формулу средней арифметической взвешенной, получаем: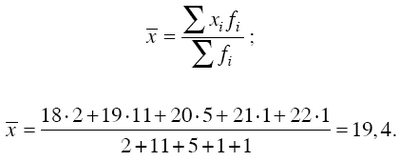

Для выбора средней арифметической взвешенной существует определенное правило: если имеется ряд данных по двум показателям, для одного из которых надо вычислить

среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя неизвестны, но могут быть найдены как произведение этих показателей, то средняя величина должна высчитывать-ся по формуле средней арифметической взвешенной.

В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины – средняя гармоническая. В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники. Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.

Например, пусть известно, что автомобиль прошел первые 210 км со скоростью 70 км/ч, а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 360 км, используя формулу средней арифметической, нельзя. Так как вариантами являются скорости на отдельных участках xj = 70 км/ч и Х2 = 75 км/ч, а весами (fi) считаются соответствующие отрезки пути, то произведения вариантов на веса не будут иметь ни физического, ни экономического смысла. В данном случае смысл приобретают частные от деления отрезков пути на соответствующие скорости (варианты xi), т. е. затраты времени на прохождение отдельных участков пути (fi/xi). Если отрезки пути обозначить через fi, то весь путь выразиться как ?fi, а время, затраченное на весь путь, – как ? fi/xi , Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени: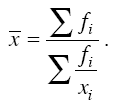

В нашем примере получим: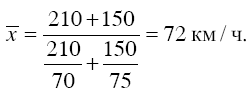

Если при использовании средней гармонической веса всех вариантов (f) равны, то вместо взвешенной можно использовать простую (невзвешенную) среднюю гармоническую:

где xi – отдельные варианты; n – число вариантов осредняемого признака. В примере со скоростью простую среднюю гармоническую можно было бы применить, если бы были равны отрезки пути, пройденные с разной скоростью.

Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина некоторого итогового, обобщающего показателя, который связан с осредняемым показателем. Так, при замене фактических скоростей на отдельных отрезках пути их средней величиной (средней скоростью) не должно измениться общее расстояние.

Форма (формула) средней величины определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым, поэтому итоговый показатель, величина которого не должна изменяться при замене вариантов их средней величиной, называется определяющим показателем. Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим. Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.

Кроме средней арифметической и средней гармонической в статистике используются и другие виды (формы) средней величины. Все они являются частными случаями степенной средней. Если рассчитывать все виды степенных средних величин для одних и тех же данных, то значения

их окажутся одинаковыми, здесь действует правило мажо-рантности средних. С увеличением показателя степени средних увеличивается и сама средняя величина. Наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в табл. 5.2.

Таблица 5.2

Виды степенных средних

Средняя геометрическая применяется, когда имеется n коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста. Средняя геометрическая простая рассчитывается по формуле

Формула средней геометрической взвешенной имеет следующий вид:

Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.

Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле

Средняя квадратическая взвешенная рассчитывается по другой формуле: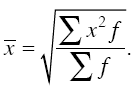

Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

Все рассмотренные выше средние величины могут быть представлены в виде общей формулы: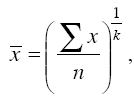

где – средняя величина; – индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.

При использовании одних и тех же исходных данных, чем больше k в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение: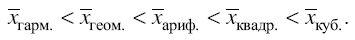

Средние величины, описанные выше, дают обобщенное представление об изучаемой совокупности и с этой точки зрения их теоретическое, прикладное и познавательное значение бесспорно. Но бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому кроме рассмотренных средних в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном (ранжированном) ряду значений признака вполне определенное положение. Среди таких величин наиболее употребительными являются структурные, или описательные, средние – мода (Мо) и медиана (Ме).

Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле

где х0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; fm_1 – частота предшествующего интервала; fm+1 – частота следующего интервала.

Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше ее. Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности. Задача нахождения медианы для дискретного вариационного ряда решается просто. Если всем единицам ряда придать порядковые номера, то порядковый номер медианного варианта определяется как (п +1) / 2 с нечетным числом членов п. Если же количество членов ряда является четным числом, то медианой будет являться среднее значение двух вариантов, имеющих порядковые номера n / 2 и n / 2 + 1.

При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле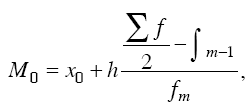

где X0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; f– число членов ряда;

?m-1 – сумма накопленных членов ряда, предшествующих данному.

Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 равных частей. Квартилей насчитывается три, а децилей – девять.

Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Эти, не очень характерные для совокупности значения вариантов, влияя на величину средней арифметической, не влияют на значения медианы и моды, что делает последние очень ценными для экономико-статистического анализа показателями.

Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения. Различают два типа рядов распределения – атрибутивные и вариационные, в зависимости от того, является ли признак, взятый за основу группировки, качественным или количественным.

Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности не постоянны, более или менее различаются между собой. Такое различие в величине признака носит название вариации. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений. Наличие вариации у отдельных единиц совокупности обусловлено влиянием большого числа факторов на формирование уровня признака. Изучение характера и степени вариации признаков у отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Для описания меры изменчивости признаков используют показатели вариации.

Другой важной задачей статистического исследования является определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности. Для решения такой задачи в статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых измеряется вариация. В практике исследователь сталкивается с достаточно большим количеством вариантов значений признака, что не дает представления о распределении единиц по величине признака в совокупности. Для этого проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда. Ранжированный ряд сразу дает общее представление о значениях, которые принимает признак в совокупности.

Недостаточность средней величины для исчерпывающей характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака. Использование этих показателей вариации дает возможность сделать статистический анализ более полным и содержательным и тем самым глубже понять сущность изучаемых общественных явлений.

Самыми простыми признаками вариации являются минимум и максимум – это наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения. Обозначим частоту повторения значения признака fi, сумма частот, равная объему изучаемой совокупности будет: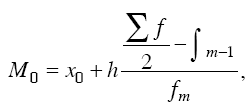

где k – число вариантов значений признака. Частоты удобно заменять частостями – wi. Частость – относительный показатель частоты – может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Формально имеем:

Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся среднее линейное отклонение, размах вариации, дисперсия, среднее квадратическое отклонение.

Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: R = Xmax – Xmin. Этот показатель дает лишь самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Он совершенно не связан с частотами в вариационном ряду, т. е. с характером распределения, а его зависимость может придавать ему неустойчивый, случайный характер только от крайних значений признака. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних величин. Область применения этого показателя ограничена достаточно однородными совокупностями, точнее, характеризует вариацию признака показатель, основанный на учете изменчивости всех значений признака.

Для характеристики вариации признака нужно обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины. Такие показатели

вариации, как среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

– абсолютное значение (модуль) отклонения варианта от средней арифметической; f– частота.

Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая – в рядах с неравными частотами.

Существует и другой способ усреднения отклонений вариантов от средней арифметической. Этот очень распространенный в статистике способ сводится к расчету квадратов отклонений вариантов от средней величины с их последующим усреднением. При этом мы получаем новый показатель вариации – дисперсию.

Дисперсия (?2) – средняя из квадратов отклонений вариантов значений признака от их средней величины: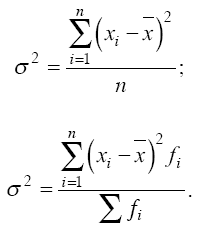

Вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).

В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение (?) представляет собой корень квадратный из дисперсии:

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражаются в тех же единицах измерения, что и варианты.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, большой интерес представляет сравнение вариаций возраста персонала и его квалификации, стажа работы и размера заработной платы и т. д. Для подобных сопоставлений показатели абсолютной колеблемости признаков – среднее линейное и среднее квадртическое отклонение – не пригодны. Нельзя, в самом деле, сравнивать колеблемость стажа работы, выражаемую в годах, с колеблемостью заработной платы, выражаемой в рублях и копейках.

При сравнении изменчивости различных признаков в совокупности удобно применять относительные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости: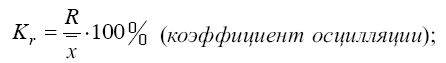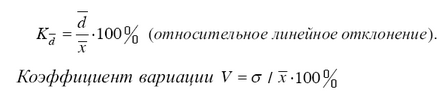

– наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному.

Статистическое наблюдение можно организовать как сплошное и несплошное. Сплошное предусматривает обследование всех единиц изучаемой совокупности явления, несплошное – лишь ее части. К несплошному относится и выборочное наблюдение.

Выборочное наблюдение является одним из наиболее широко применяемых видов несплошного наблюдения. В основе этого наблюдения лежит идея о том, что отобранная в случайном порядке некоторая часть единиц может представлять всю изучаемую совокупность явления по интересующим исследователя признакам. Целью выборочного наблюдения является получение информации прежде всего для определения сводных обобщающих характеристик всей изучаемой совокупности. По своей цели выборочное наблюдение совпадает с одной из задач сплошного наблюдения, и поэтому встает вопрос о том, какое из двух видов наблюдения – сплошное или выборочное – целесообразнее провести.

При решении этого вопроса необходимо исходить из следующих основных требований, предъявляемых к статистическому наблюдению:

• информация должна быть достоверной, т. е. максимально соответствовать реальной действительности;

• сведения должны быть достаточно полными для решения задач исследования;

• отбор информации должен быть проведен в максимально сжатые сроки для использования ее в оперативных целях;

• денежные и трудовые затраты на организацию и проведение должны быть минимальными.

При выборочном наблюдении эти требования обеспечиваются в большей мере, чем при сплошном. Преимущества этого метода по сравнению со сплошным можно оценить, если оно организовано и проведено в строгом соответствии с научными принципами теории выборочного метода, а именно обеспечение случайности отбора единиц и достаточного их числа. Соблюдение этих принципов позволяет получить такую совокупность единиц, которая представляет всю изучаемую совокупность по интересующим исследователя признакам, т. е. является репрезентативной (представительной).

При проведении выборочного наблюдения обследуются не все единицы изучаемого объекта, т. е. не все единицы совокупности, а лишь некоторая специально отобранная часть. Первый принцип отбора– обеспечение случайности – заключается в том, что при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку. Случайный отбор – это не беспорядочный отбор, а отбор при соблюдении определенной методики, например осуществление отбора по жребию, применение таблицы случайных чисел и т. д.

Второй принцип отбора – обеспечение достаточного числа отобранных единиц – тесно связан с понятием репрезентативности выборки. Так как любое выборочное наблюдение проводится с определенной целью и четко сформулированными конкретными задачами, то понятие репрезентативности как раз и связано с целью и задачами исследования. Отобранная из всей изучаемой совокупности часть должна быть репрезентативной прежде всего в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.

В выборочном наблюдении используются понятия «ге-нералъная совокупность» – изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» – случайно отобранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т. е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности. Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадрати-ческие отклонения, мода и медиана и др.

Исследователя могут интересовать и распределения единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.

Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.

Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения, для любой выборки заданного объема.

Таким образом, цель выборочного метода – сделать вывод о значении признаков генеральной совокупности на основе информации случайной выборки из этой совокупности.

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака происходит из-за ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими. Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения практически определить очень сложно, а иногда и невозможно, поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.

Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появление такой ошибки, необходимо соблюдать принцип случайности отбора единиц.

Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появление таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.

Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки является теория вероятностей и ее предельные теоремы.

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностями (~ —), которое не превышает ±. Предельной ошибкой выборки принято считать максимально возможное расхождение (~ —), т. е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П.Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле

– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле

В математической статистике употребляют коэффициент доверия t, значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности (табл. 6.1).

Таблица 6.1

Коэффициент доверия t и соответствующие уровни доверительной вероятности

Коэффициент доверия позволяет вычислить предельную ошибку выборки,

т. е. предельная ошибка выборки равна t-кратному числу средних ошибок выборки.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью. Как видно из последней графы табл. 6.1, вероятность появления ошибки равной или большей утроенной средней ошибки выборки, т. е. 

крайне мала и равна 0,003(1–0,997). Такие маловероятные события считаются практически невозможными, а потому величину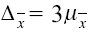

можно принять за предел возможной ошибки выборки.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней, которая показывает (с определенной вероятностью), насколько выборочная величина может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна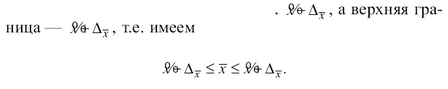

Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.

Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объем единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (А), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем: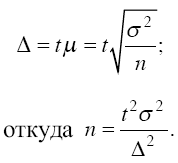

Суть этой формулы – в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t2) и дисперсии вариационного признака (?2) и обратно пропорционален квадрату предельной ошибки выборки (?2). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки может быть уменьшена в четыре раза. Из трех параметров два (t и ?) задаются исследователем. При этом исследователь исходя из цели

и задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (?), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, поэтому в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.

Наиболее сложно установить при проектировании выборочного наблюдения третий параметр в формуле (5.2) – дисперсию выборочной совокупности. В этом случае необходимо использовать всю информацию, имеющуюся в распоряжении исследователя, полученную в ранее проведенных подобных и пробных обследованиях.

Вопрос об определении необходимой численности выборки усложняется, если выборочное обследование предполагает изучение нескольких признаков единиц отбора. В этом случае средние уровни каждого из признаков и их вариация, как правило, различны, и поэтому решить вопрос о том, дисперсии какого из признаков отдать предпочтение, возможно лишь с учетом цели и задач обследования.

При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.

В целом формула предельной ошибки выборочной средней величины позволяет определять:

• величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;

• необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой заданной величины;

• вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.

В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.

В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки:

собственно случайную;

механическую;

типическую (стратифицированную, районированную);

серийную (гнездовую);

комбинированную;

многоступенчатую;

многофазную;

взаимопроникающую.

Собственно случайная выгборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц.

Случайный порядок подобен жеребьевке. На практике он чаще всего применяется при использовании специальных таблиц случайных чисел. Если, например, из совокупности, содержащей 1587 единиц, следует отобрать 40 единиц, то из таблицы отбирают 40 четырехзначных чисел, которые меньше 1587.

В том случае, когда собственно случайная выборка организуется как повторная, расчет стандартной ошибки производится в соответствии с формулой (6.1). При бесповторном способе отбора формула для расчета стандартной ошибки будет: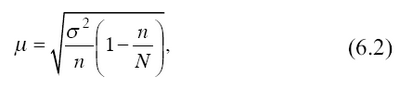

где 1 – n / N – доля единиц генеральной совокупности, не попавших в выборку. Так как эта доля всегда меньше единицы, то ошибка при бесповторном отборе при прочих равных условиях всегда меньше, чем при повторном. Бесповторный отбор организовать легче, чем повторный, и он применяется намного чаще. Однако величину стандартной ошибки при бесповторном отборе можно определять по более простой формуле (5.1). Такая замена возможна, если доля единиц генеральной совокупности, не попавших в выборку, большая и, следовательно, величина близка к единице.

Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности. Довольно часто генеральная совокупность такая большая, что провести подобную предварительную работу чрезвычайно сложно и нецелесообразно, поэтому на практике применяют другие виды выборок, каждая из которых не является строго случайной. Однако организуются они так, чтобы было обеспечено максимальное приближение к условиям случайного отбора.

При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения. Однако практически легче организовать механическую выборку, чем собственно случайную, и при проведении выборочных обследований чаще всего пользуются этим видом выборки. Стандартную ошибку при механической выборке определяют по формуле собственно случайной бесповторной выборки (6.2).

Типическая (районированная, стратифицированная) выборка преследует две цели:

• обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам;

• увеличить точность результатов выборочного обследования.

При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут содержать одинаковое или различное число единиц отбора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке, как с равной, так и неравной долей отбора, удается устранить влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть не от величины общей дисперсии ?2, а от величины средней из групповых дисперсий ?i2. Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки.

При определении стандартных ошибок типической выборки применяются следующие формулы:

• при повторном способе отбора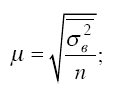

• при бесповторном способе отбора: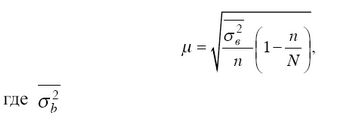

– средняя из групповых дисперсий в выборочной совокупности.

Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство. Стандартная ошибка серийной выборки определяется по формулам:

• при повторном способе отбора -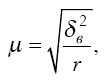

где ?– межсерийная дисперсия выборочной совокупности; r – число отобранных серий;

• при бесповторном способе отбора -

где R – число серий в генеральной совокупности.

В практике те или иные способы и виды выборок применяются в зависимости от цели и задач выборочных обследований, а также возможностей их организации и проведения. Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированные. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно случайной и т. д. К комбинированной выборке прибегают для обеспечения наибольшей репрезентативности с наименьшими трудовыми и денежными затратами на организацию и проведение обследования.

При комбинированной выборке величина стандартной ошибки выборки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле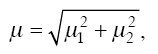

где ?1 и ?2 – стандартные ошибки соответственно механической и типической выборок.

Особенность многоступенчатой выгборки состоит в том, что выборочная совокупность формируется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного способа и вида отбора отбираются единицы первой ступени. На второй ступени из каждой единицы первой ступени, попавшей в выборку, отбираются единицы второй ступени и т. д. Число ступеней может быть и больше двух. На последней ступени формируется выборочная совокупность, единицы которой подлежат обследованию. Так, например, для выборочного обследования бюджетов домашних хозяйств на первой ступени отбираются территориальные субъекты страны, на второй – районы в отобранных регионах, на третьей – в каждом муниципальном образовании отбираются предприятия или организации и, наконец, на четвертой ступени – в отобранных предприятиях отбираются семьи.

Таким образом, выборочная совокупность формируется на последней ступени. Многоступенчатая выборка более гибкая, чем другие виды, хотя в общем она дает менее точные результаты, чем выборка того же объема, но сформированная в одну ступень. Однако при этом она имеет одно важное преимущество, которое заключается в том, что основу выборки при многоступенчатом отборе нужно строить на каждой из ступеней только для тех единиц, которые попали в выборку, а это очень важно, так как нередко готовой основы выборки нет.

Стандартную ошибку выборки при многоступенчатом отборе при группах разных объемов определяют по формуле

где ?1, ?2, ?3, ... – стандартные ошибки на разных ступенях;

n1, n2, n3, ... – численность выборок на соответствующих ступенях отбора.

В том случае, если группы неодинаковы по объему, то теоретически этой формулой пользоваться нельзя. Но если общая доля отбора на всех ступенях постоянна, то практически расчет по этой формуле не приведет к искажению величины ошибки.

Сущность многофазной выгборки состоит в том, что на основе первоначально сформированной выборочной совокупности образуют подвыборку, из этой подвыборки – следующую подвыборку и т. д. Первоначальная выборочная совокупность представляет собой первую фазу, подвыборка из нее – вторую и т. д. Многофазную выборку целесообразно применять в случаях, если:

для изучения различных признаков требуется неодинаковый объем выборки;

колеблемость изучаемых признаков неодинакова и требуемая точность различна;

в отношении всех единиц первоначальной выборочной совокупности (первая фаза) необходимо собрать менее подробные сведения, а в отношении единиц каждой последующей фазы – более подробные.

Одним из несомненных достоинств многофазной выборки является то обстоятельство, что сведениями, полученными на первой фазе, можно пользоваться как дополнительной информацией на последующих фазах, информацией второй фазы – как дополнительной информацией на следующих фазах и т. д. Такое использование сведений повышает точность результатов выборочного обследования.

При организации многофазной выборки можно применять сочетание различных способов и видов отбора (типическую выборку с механической и т. д.). Многофазный отбор можно сочетать с многоступенчатым. На каждой ступени выборка может быть многофазной.

Стандартная ошибка при многофазной выборке рассчитывается на каждой фазе в отдельности в соответствии с формулами того способа отбора и вида выборки, при помощи которых формировалась ее выборочная совокупность.

Взаимопроникающие выгборки – это две или более независимые выборки из одной и той же генеральной совокупности, образованные одним и тем же способом и видом. К взаимопроникающим выборкам целесообразно прибегать, если необходимо за короткий срок получить предварительные итоги выборочных обследований. Взаимопроникающие выборки эффективны для оценки результатов обследования. Если в независимых выборках результаты одинаковы, то это свидетельствует о надежности данных выборочного обследования. Взаимопроникающие выборки иногда можно применять для проверки работы различных исследователей, поручив каждому из них провести обследование разных выборок.

Стандартная ошибка при взаимопроникающих выборках определяется по той же формуле, что и типическая пропорциональная выборка (5.3). Взаимопроникающие выборки по сравнению с другими видами требуют больших трудовых затрат и денежных расходов, поэтому исследователь должен учитывать это обстоятельство при проектировании выборочного обследования.

Предельные ошибки при различных способах отбора и видах выборки определяются по формуле ? = t?, где ? – соответствующая стандартная ошибка.

В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, исследуется роль отдельных факторов в формировании важнейших экономических показателей, индексы используются также в международных сопоставлениях экономических показателей, определении уровня жизни, мониторинге деловой активности в экономике и т. д.

Индекс (лат. index) – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различия условий может проявляться во времени (индексы динамики), в пространстве (территориальные индексы) и в выборе в качестве базы сравнения какого-либо условного уровня.

По охвату элементов совокупности (ее объектов, единиц и их признаков) различают индексы индивидуальные (элементарные) и сводные (сложные), которые в свою очередь делятся на общие и групповые.

Индивидуальные индексы – это результат сравнения двух показателей, относящихся к одному объекту, например сравнение цен какого-либо товара, объема его реализации и т. д. В статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индивидуальные индексы качественных и количественных показателей. На-

пример, индекс цен ip = P1 / P0 характеризует относительное изменение уровня цены единицы каждого вида продукции в отчетном периоде по сравнению с базисным и является качественным показателем.

Индекс физического объема iq = q1 / q2 показывает, во сколько раз изменилось производство данного вида продукции в отчетном периоде по отношению к периоду, с которым проводилось сравнение, и является количественным показателем.

Сводный индекс характеризует соотношение уровней нескольких элементов совокупности (например, изменение объема выпуска нескольких видов продукции, имеющих различную натурально-вещественную форму, или изменение уровня производительности труда при производстве нескольких видов продукции). Если изучаемая совокупность состоит из нескольких групп, то сводные индексы, каждый из которых характеризует изменение уровней отдельной группы единиц, являются групповы1ми (субиндексами), а сводный индекс, охватывающий всю совокупность единиц, – общим (тотальныгм) индексом. Сводные индексы выражают соотношение сложных социально-экономических явлений и состоят из двух частей: индексируемой величины и соизмерителя, который называется весом.

Показатель, изменение которого характеризует индекс, называется индексируемым. Индексируемые показатели могут быть двоякого рода. Одни из них измеряют общий, суммарный размер (объем) того или иного явления и условно называются объемныгми, экстенсивныгми (физический объем продукции данного вида, численность работников, общие затраты труда на производство продукции, общая себестоимость продукции и т. п.). Эти показатели получаются как итог непосредственного подсчета или суммирования и являются исходными, первичными.

Другие показатели измеряют уровень явления или признака в расчете на ту или иную единицу совокупности и условно называются качественныжи, интенсивныши: выработка продукции в единицу времени (или на одного работника), затраты рабочего времени на единицу продукции, себестоимость единицы продукции и т. д. Эти показатели получаются путем деления объемных показателей, т. е. носят расчетный, вторичный характер. Они измеряют интенсивность, эффективность явления или процесса и, как правило, являются либо средними, либо относительными величинами.

При использовании индексного метода применяется определенная символика, т. е. система условных обозначений. Каждый индексируемый показатель обозначается определенной буквой (обычно латинской). Введем следующие условные обозначения:

Q – количество (объем) произведенной продукции (или количество проданного товара) данного вида в натуральном выражении;

Т – общие затраты рабочего времени (труда) на производство продукции данного вида, измеряемые в человеко-часах или человеко-днях; в некоторых случаях этой же буквой обозначается среднее списочное число работников;

z – себестоимость единицы продукции;

t – трудоемкость единицы продукции;

p – цена единицы продукции или товара;

– общий расход сырья, материала или топлива на производство продукции данного вида и объема.

Показатели за базисный период имеют в формулах подстрочный знак «0», а за сравниваемый (текущий, отчетный) период – знак «1». Индивидуальные индексы обозначаются буквой i и тоже снабжаются подстрочным знаком – обозначением индексируемого показателя. Так, iQ означает индивидуальный индекс количества (физического объема) произведенной продукции (или проданного товара) данного вида; iz – индивидуальный индекс себестоимости единицы продукции данного вида и т. п.

Сводные индексы обозначаются буквой I и также сопровождаются подстрочными значками показателей, изменение которых они характеризуют. Например, It – сводный индекс трудоемкости единицы продукции и т. д.

Индивидуальные индексы являются обычными относительными величинами, т. е. могут быть названы индексами только в широком понимании этого термина. Индексы в узком смысле, или собственно индексы, – это тоже показатели относительные, но особого рода. Они имеют более сложную методику построения и расчета, а специфические приемы их построения и составляют суть индексного метода.

Социально-экономические явления и характеризующие их показатели могут быть соизмеримыми, т. е. иметь общую меру, и несоизмеримыми. Так, объем продукции или товара одного и того же вида и сорта, произведенные на разных предприятиях или проданные в разных магазинах, соизмеримы и могут суммироваться, а объемы разных видов продукции или товаров несоизмеримы и непосредственно суммироваться не могут. Нельзя, например, складывать килограммы хлеба с литрами молока, метрами ткани и парами обуви. Несоизмеримость и невозможность непосредственного суммирования при построении и расчете сводного индекса объясняется здесь не столько различием натуральных единиц измерения, сколько различием потребительских свойств, неодинаковой натурально-вещественной формой этих продуктов или товаров.

В связи с этим для исчисления сводных индексов необходимо привести их составные части к сопоставимому виду. Единство различных видов продукции или разных товаров состоит в том, что они являются продуктами труда, имеют определенную стоимость и ее денежное выражение – цену (p). Каждый продукт имеет также ту или иную себестоимость (z) и трудоемкость (t). Эти качественные показатели и могут быть использованы в качестве общей меры – коэффициентов соизмерения разнородных продуктов. Умножая объем продукции каждого вида (Q) на соответствующую цену, себестоимость или трудоемкость единицы продукции, мы сведем различные продукты к одному и тому же единству и получим сравнимые показатели.

Аналогично обстоит дело и при построении сводных индексов качественных показателей. Пусть, например, нас интересует изменение общего уровня цен на различные проданные товары. Хотя формально цены разных товаров соизмеримы, однако непосредственное их суммирование без учета количества проданного товара каждого вида дает величину, лишенную самостоятельного практического значения. Поэтому сводный индекс цен нельзя построить как отношение простых сумм: ip = ?p1/?p2. Цены отдельных товаров не учитывают конкретного количества проданных товаров и их статистического веса и роли в процессе товарооборота. Простые суммы цен отдельных товаров непригодны для построения сводного индекса еще и потому, что цены зависят от единицы измерения товаров, изменение которых даст другие суммы и другую величину индекса.

Следовательно, при построении сводных индексов качественных показателей их нельзя рассматривать в отрыве от связанных с ними объемных показателей, в расчете на единицу которых вычислены эти качественные показатели. Только умножив тот или иной качественный показатель (p, z, t) на непосредственно связанный с ними объемный показатель (Q), мы сможем учесть роль и статистический вес каждого вида продукции (или товара) в том или ином экономическом процессе – процессе образования общей стоимости (pQ), общей себестоимости (zQ), общих затрат рабочего времени (tQ) и т. п. Вместе с тем мы получим показатели, суммирование которых имеет практическую значимость.

Таким образом, первая особенность индексного метода и собственно индексов состоит в том, что индексируемый показатель рассматривается не изолированно, а во взаимосвязи с другими показателями.

Умножая индексируемый показатель на другой, связанный с ним, мы сводим различные явления к их единству, обеспечиваем их количественную сравнимость и учитываем их вес в реальном экономическом процессе. Поэтому показатели-сомножители, связанные с индексируемыми показателями, принято называть весами индексов, а умножение на них – взвешиванием.

Однако умножение значений индексируемого показателя на связанные с ними значения другого показателя (веса) еще не решает проблему собственно индекса. Умножив, например, цены на соответствующие им количества товаров, мы найдем стоимость этих товаров в каждом периоде и тем самым решим проблему соизмерения и взвешивания. Однако сопостав-ление полученных сумм произведений (?p1Q1 и ?p0Q0) дает показатель, который характеризует изменение товарооборота, зависящего от двух факторов – цен и количества (объема) товаров, но не дает характеристику изменения уровня цен и уровня производства товаров:

Для того чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить в формуле (7.1) изменение другого фактора, зафиксировав его как в числителе, так и в знаменателе на уровне одного и того же периода. Например, для оценки объема разнородной продукции в двух сравниваемых периодах нужно оценить товары, проданные в обоих периодах по одним и тем же, например базисным, ценам (р0). Полученный показатель отразит изменение только одного фактора – физического объема продукции Q:

А для оценки изменения уровня цен на группу товаров нужно сопоставлять одинаковые объемы этих товаров, т. е. количество товаров (Q) зафиксировать и в числителе, и в знаменателе индекса на одном и том же уровне (либо на базисном, либо на отчетном). Таким образом, построенные сводные индексы цен будут характеризовать только изменение цен, т. е. индексируемого показателя, так как изменение весов (Q) будет устранено (элиминировано) благодаря их фиксированию: Ip =?p1q1/?p0q1; Ip =?p1q0/?p0q0.

В обоих случаях (Iq и Ip) индекс отразил изменение только одного фактора – индексируемого показателя благодаря фиксированию другого (весов) на одном и том же уровне. Элиминирование влияния изменения весов путем их фиксирования в числителе и знаменателе индекса на одном и том же уровне – вторая особенность индексов и индексного метода.

Рассматривая проблемы, возникающие при построении собственно индексов, ставилась задача дать сравнительную характеристику уровней сложного явления, состоящего из разнородных элементов (разные виды продукции и т. п.). Так, Ip должен показать, как изменился в целом уровень цен, т. е. измерить динамику цен различных товаров в виде одного обобщающего показателя. Исторически собственно индексы появились как результат решения именно этой экономической задачи – задачи обобщения, синтеза динамики отдельных элементов сложного явления в одном обобщающем показателе, сводном индексе.

Однако собственно индексы используются для решения и другой задачи – анализа влияния изменения отдельных показателей-факторов на изменение показателя, представляющего функцию этих факторов-аргументов. Так, общая стоимость проданных товаров (товарооборот – ?pq) есть функция их цен (р) и количеств (объемов – Q), поэтому можно поставить задачу измерить влияние каждого из этих факторов на изменение товарооборота, т. е. определить, как он изменился отдельно за счет изменения каждого фактора. Индексы, применяемые для решения подобных аналитических задач, также строятся с использованием специфических особенностей индексного метода – взвешивания и элиминирования изменения весов.

Таким образом, собственно индекс – это относительный показатель особого рода, в котором уровни социально-экономического явления рассматриваются в связи с другим (или другими) явлением, изменение которого при этом элиминируется. Показатели, связанные с индексируемым показателем, используются в качестве весов индекса, а взвешивание и элиминирование изменения весов (фиксирование в числителе и знаменателе индекса на одном и том же уровне) составляют специфику собственно индексов и индексного метода.

Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу измерения которого он исчисляется (или к единице измерения которого относится). Так, цена единицы товара связана с его количеством (Q); с объемом произведенной продукции связаны такие качественные показатели, как цена (р), себестоимость (z) и трудоемкость (t = T / Q) единицы продукции, а также удельный расход сырья, материалов (m = M / Q).

Сводные индексы качественных показателей должны характеризовать не их изменение вообще применительно к какому-либо произвольному набору товаров или продукции, а изменение цен, себестоимости, трудоемкости или удельных расходов вполне определенного количества произведенной продукции или проданных товаров. Это и достигается путем взвешивания – умножения уровней индексируемого качественного показателя на значения связанного с ним объемного показателя (веса) – и фиксирования весов в числителе и знаменателе индекса на одном и том же уровне. Сопоставление сумм таких произведений дает агрегатный индекс. Аналогично могут быть построены агрегатные индексы динамики себестоимости и трудоемкости единицы продукции, а также индекс удельного расхода сырья или материала.

Основной проблемой при построении этих сводных индексов является экономически обоснованный выбор уровня, на котором нужно зафиксировать веса индекса, т. е. в данном случае объем продукции (или товаров) – Q.

Обычно перед сводным индексом динамики качественного показателя ставится задача измерить не только относительное изменение уровня, но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения: сумму экономии покупателей за счет снижения цен (или сумму их дополнительных расходов, если цены повысились), сумму экономии (или дополнительных затрат) за счет изменения себестоимости и т. п.

Такая постановка задачи приводит к индексам динамики качественных показателей с весами текущего периода:

• во-первых, исследователя интересует изменение себестоимости или трудоемкости той продукции, которая выпущена в настоящее время, а не в прошлом;

• во-вторых, экономический эффект должен быть увязан с фактическими результатами текущего, отчетного, а не предыдущего (базисного) периода.

В качестве примера приведем агрегатный индекс себестоимости: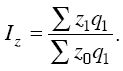

Таким образом, в этом индексе числитель представляет собой сумму фактических затрат на продукцию в отчетном периоде, а знаменатель – условную величину, которая показывает, сколько средств было бы затрачено на продукцию отчетного периода, если бы себестоимость единицы каждого вида продукции сохранялась на базисном уровне.

Реальный экономический эффект, полученный за счет изменения себестоимости единицы продукции, выражается абсолютной величиной, которая вычисляется как разность между суммами в числителе и знаменателе индекса: (?z1Q1 ??z0Q1) или (? z1?z0 Q1).

Следовательно, взвешивание по весам отчетного (текущего) периода увязывает индекс качественного показателя с показателем экономического эффекта, который получен за счет изменения индексируемого показателя. Поэтому агре-гатныге индексы! динамики качественный показателей строятся и вычисляются обычно с весами отчетного периода: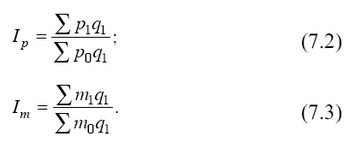

Формула (7.2) представляет собой сводный индекс цен, а формула (7.3) – расчет сводного индекса расхода материалов. В этих индексах разность между числителем и знаменателем характеризует в первом случае уменьшение либо увеличение затрат на приобретение одного и того же набора товаров в зависимости от знака разности; во втором случае – увеличение или уменьшение расхода материалов на производство одного и того же объема продукции.

Объемные показатели могут быть соизмеримыми (Т, рQ, zQ) и несоизмеримыми (объем продукции или товаров разного вида – Q). Соизмеримые объемные показатели могут непосредственно суммироваться, и построение агрегатных индексов не вызывает трудностей.

Для получения общего итога и построения агрегатного индекса несоизмеримого объемного показателя нужно предварительно соизмерить отдельные значения этого показателя. Исходя из экономической сущности явления, нужно найти общую меру и использовать ее в качестве коэффициента соизмерения. Такой общей мерой для объемных показателей являются связанные с ними качественные показатели. Так, объемы различных видов продукции могут быть соизмерены с помощью цены (р), себестоимости (z) и трудоемкости (t) этих продуктов. Умножая индексируемый объемный показатель на тот или иной качественный показатель, не только обеспечивается возможность суммирования, но одновременно учитывается также роль каждого элемента, например продукта, в реальном экономическом процессе, т. е. его статистический вес в этом процессе.

Поскольку в индексе объемного показателя в качестве весов могут выступать различные качественные показатели, возникает вопрос о том, какой же именно их них следует использовать. Этот вопрос в каждом конкретном случае должен решаться в соответствии с той познавательной экономической задачей, которая ставится перед индексом, т. е. выбор тех или иных весов-соизмерителей должен быть обоснован экономически.

В практике экономической и статистической работы в качестве весов агрегатного индекса объема продукции обычно используются цены. Так строятся индексы объема промышленной и сельскохозяйственной продукции, а также индексы физического объема товарооборота.

В ряде случаев изменение объема продукции интересует не само по себе, а с точки зрения его влияния на изменение показателя более сложного порядка: общей стоимости продукции, общей ее себестоимости, общих затрат рабочего времени, общего объема производства на данном его участке и т. п. В таких случаях выбор весов-соизмерителей определяется взаимосвязью показателей-факторов, от которых зависит более сложный показатель.

Чтобы индекс отражал только изменение индексируемого объемного показателя, веса в его числителе и знаменателе фиксируются на уровне одного и того же периода. В практике экономической работы в индексах динамики объемных показателей веса обычно фиксируются на уровне базисного периода (см. формулу 7.2). Это обеспечивает возможность построения систем взаимосвязанных индексов.

Для индивидуальных объемных показателей (объем реализации, объем производительности продукции, посевная площадь) веса выбираются на уровне базисного периода. Например:

где In– сводный индекс урожайности; I – сводный индекс стоимости товарооборота; Iq – сводный индекс себестоимости.

В отличие от индексов качественных показателей, которые исчисляются по сравнимому кругу единиц (сравнимой продукции), сводные индексы объемных показателей в целях полноты и точности должны охватывать весь круг единиц, произведенных (или проданных) в каждом периоде. В связи с этим возникает вопрос о том, какие значения весов следует брать для тех видов продукции, которые в одном из сравниваемых периодов не производились.

В практике статистики в таких случаях применяются два способа. При расчете индексов объема промышленной продукции новые ее виды, для которых нет цен базисного периода, оцениваются условно по ценам текущего периода. При расчете же индексов объема проданных товаров используется метод, основанный на условном предположении, что и цены на новые товары изменились в той же степени, что цены на сравниваемый круг аналогичных товаров.

При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисныгх индексов сравнение индексируемого показателя в каждом индексе производится с уровнем одного и того же периода, а в ряду цепныгх индексов индексируемый показатель сопоставляется с уровнем предыдущего периода.

В каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне. Если же строится ряд индексов, то веса в нем могут быть либо постоянными для всех индексов ряда, либо переменными.

Ряд базисных индексов объема продукции ?q1p0/?q0p0,?q2p0/?q0p0,?q3p0/?q0p0 и т. д. имеет постоянные веса (р0). Постоянные веса (р0) имеет и ряд цепных индексов: ?q1p0/?q0p0,?q2p0/?q1p0,?q3p0/?q2p0 и т. д.

Ряд цепных индексов цен ?p1q1/?p1q0,?p2q2/?p2q0, ?p3q3 /?p3q2 и т. д. построен с переменными весами (в 1-м индексе – q1 во 2-м – q2 и т. д.).

Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):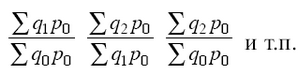

Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных индексов к базисным, и наоборот. Поэтому ряды индексов объема продукции и объема проданных товаров строятся в статистической практике с постоянными весами. Так, в индексах объема продукции в качестве постоянных весов используются цены, зафиксированные на уровне, который был установлен на 1 января какого-либо базисного года. Такие цены, используемые в течение ряда лет, называются сопо-ставимыгми (фиксированнылми).

Использование в индексах объема продукции (товаров) сопоставимых цен позволяет путем простого суммирования получать итоги за несколько лет. Сопоставимые цены не должны сильно отличаться от действующих (текущих) цен, поэтому их периодически пересматривают, переходя к новым сопоставимым ценам. Чтобы иметь возможность исчислять индексы объема продукции за длительные периоды, в течение которых применялись различные сопоставимые цены, продукцию одного года оценивают как в прежних, так и в новых фиксированных ценах. Индекс за длительный период исчисляют цепным методом, т. е. путем перемножения индексов за отдельные отрезки этого периода.

Ряды индексов качественных показателей, которые экономически правильно взвешивать по весам текущего периода, строятся с переменными весами.

При построении территориальных индексов, т. е. при сравнении показателей в пространстве (межрайонные, сравнение между разными предприятиями и др.), возникают вопросы о выборе базы сравнения и района (объекта), на уровне которого следует зафиксировать веса индекса. В каждом конкретном случае эти вопросы нужно решать исходя из задач исследования. Выбор базы сравнения зависит, в частности, от того, будут ли сравнения двусторонними (например, сравнение показателей двух соседних территориальных единиц) или многосторонними (сравнение показателей нескольких территорий, объектов).

При двусторонних сравнениях каждая территория или объект с одинаковым основанием может быть принят как в качестве сравниваемого, так и в качестве базы сравнения. В связи с этим возникает вопрос о фиксировании весов сводного индекса на уровне того или иного района (объекта). Пусть, например, нужно определить, в какой из двух областей и насколько процентов ниже себестоимость единицы продукции и больше объем ее производства.

Если сравнивать область А с областью Б, достаточно обоснованный и простой путь состоит в том, чтобы зафиксировать в индексе себестоимости в качестве весов объемы продукции в целом по обеим территориям (Q = QA + QБ), тогда получим: Iz =?zQ/?zQ.

При многосторонних сравнениях, например при сравнениях качественных показателей по нескольким областям, нужно, соответственно, расширить и границы территории, на уровне которой фиксируются веса.

В сводных территориальных индексах объемных показателей в качестве весов могут быть приняты средние уровни соответствующих качественных показателей, вычисленные в целом по сравниваемым территориям. Так, в нашем примере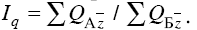

В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.

Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема: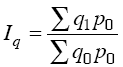

(агрегатная форма индекса Ласпейреса).

Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс: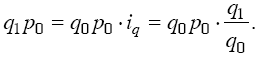

Тогда формула сводного индекса примет вид:

т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.

Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (г^) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше: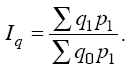

Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq , тогда: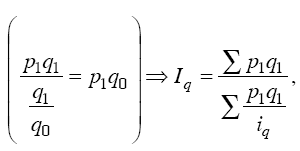

таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругу единиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).

Явления общественной жизни, изучаемые социально-экономической статистикой, находятся в непрерывном изменении и развитии. С течением времени – от месяца к месяцу, от года к году – изменяются численность населения и его состав, объем производимой продукции, уровень производительности труда и т. д., поэтому одной из важнейших задач статистики является изучение изменения общественных явлений во времени – процесса их развития, их динамики. Эту задачу статистика решает путем построения и анализа рядов динамики (временных рядов).

Ряд динамики (хронологический, динамический, временной ряд) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд включает два обязательных элемента: время и конкретное значение показателя (уровень ряда).

Каждое числовое значение показателя, характеризующее величину, размер явления, называется уровнем ряда. Кроме уровней каждый ряд динамики содержит указания о тех моментах либо периодах времени, к которым относятся уровни.

При подведении итогов статистического наблюдения получают абсолютные показатели двух видов. Одни из них характеризуют состояние явления на определенный момент времени: наличие на этот момент каких-либо единиц сово-

купности или наличие того или иного объема признака. К таким показателям относится численность населения, парк автомобилей, жилищный фонд, товарные запасы и т. д. Величину таких показателей можно определить непосредственно только по состоянию на тот или иной момент времени, а потому эти показатели и соответствующие ряды динамики и называются моментными.

Другие показатели характеризуют итоги какого-либо процесса за определенный период (интервал) времени (сутки, месяц, квартал, год и т. п.). Такими показателями являются, например, число родившихся, количество произведенной продукции, ввод в действие жилых домов, фонд заработной платы и др. Величину этих показателей можно подсчитать только за какой-нибудь интервал (период) времени, поэтому такие показатели и ряды их значений называются интервальными.

Из различного характера интервальных и моментных абсолютных показателей вытекают некоторые особенности (свойства) уровней соответствующих рядов динамики. В интервальном ряду величина уровня, представляющего собой итог какого-либо процесса за определенный интервал (период) времени, зависит от продолжительности этого периода (длины интервала). При прочих равных условиях уровень интервального ряда тем больше, чем больше длина интервала, к которому этот уровень относится.

В моментных же рядах динамики, где тоже есть интервалы – промежутки времени между соседними в ряду датами, – величина того или иного конкретного уровня не зависит от продолжительности периода между соседними датами.

Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени. При этом единица совокупности, входящая в состав одного уровня, не входит в состав других уровней, поэтому в интервальном ряду динамики уровни за примыкающие друг к другу периоды времени можно суммировать, получая итоги (уровни) за более продолжительные периоды (так, суммируя месячные уровни, получим квартальные, суммируя квартальные, получим годовые, суммируя годовые – многолетние).

Иногда путем последовательного сложения уровней интервального ряда за примыкающие друг к другу интервалы времени строится ряд нарастающих итогов, в котором каждый уровень представляет собой итог не только за данный период, но и за другие периоды, начиная с определенной даты (с начала года и т. д.). Такие нарастающие итоги нередко приводятся в бухгалтерских и других отчетах предприятий.

В моментном динамическом ряду одни и те же единицы совокупности обычно входят в состав нескольких уровней, поэтому суммирование уровней моментного ряда динамики само по себе не имеет смысла, так как получающиеся при этом итоги лишены самостоятельной экономической значимости.

Выше говорилось о рядах динамики абсолютных величин, являющихся исходными, первичными. Наряду с ними могут быть построены ряды динамики, уровни которых являются относительными и средними величинами. Они также могут быть либо моментными, либо интервальными. В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются путем деления других величин.

При построении и перед анализом ряда динамики нужно прежде всего обратить внимание на то, чтобы уровни ряда были сопоставимы между собой, так как только в этом случае динамический ряд будет правильно отражать процесс развития явления. Сопоставимость уровней ряда динамики – это важнейшее условие обоснованности и правильности выводов, полученных в результате анализа этого ряда. При построении динамического ряда надо иметь в виду, что ряд может охватывать большой период времени, в течение которого могли произойти изменения, нарушающие сопоставимость (территориальные изменения, изменения круга охвата объектов, методологии расчетов и т. д.).

При изучении динамики общественных явлений статистика решает следующие задачи:

• измеряет абсолютную и относительную скорость роста либо снижения уровня за отдельные промежутки времени;

• дает обобщающие характеристики уровня и скорости его изменения за тот или иной период;

• выявляет и численно характеризует основные тенденции развития явлений на отдельных этапах;

• дает сравнительную числовую характеристику развития данного явления в разных регионах или на разных этапах;

• выявляет факторы, обусловливающие изменение изучаемого явления во времени;

• делает прогнозы развития явления в будущем.

При изучении динамики используются различные показатели и методы анализа, как элементарные, более простые, так и более сложные, требующие соответственно применения более сложных разделов математики.

Простейшими показателями анализа, которые используются при решении ряда задач, в первую очередь при измерении скорости изменения уровня ряда динамики, являются абсолютный прирост, темпы роста и прироста, а также абсолютное значение (содержание) одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, называется базисным, так как он является базой сравнения. Обычно за базу сравнения принимается либо предыдущий, либо какой-либо предшествующий уровень, например первый уровень ряда.

Если каждый уровень сравнивается с предыдущим, то полученные при этом показатели называются цепными, так как они представляют собой как бы звенья «цепи», связывающей между собой уровни ряда. Если же все уровни связываются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.

Часто построение ряда динамики начинают с того уровня, который будет использован в качестве постоянной базы сравнения. Выбор этой базы должен быть обоснован историческими и социально-экономическими особенностями развития изучаемого явления. В качестве базисного целесообразно брать какой-либо характерный, типичный уровень, например конечный уровень предыдущего этапа развития (или средний его уровень, если на предыдущем этапе уровень то повышался, то понижался).

Абсолютныш прирост показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, т. е. за тот или иной промежуток (период) времени. Абсолютный прирост равен разности между сравниваемыми уровнями и измеряется в тех же единицах, что и эти уровни:

? =yi?yi?1;

? =yi ?y0 ,

где уi – уровень i-го года; yi-1 – уровень предшествующего года; y0 – уровень базисного года. Если уровень уменьшился по сравнению с базисным, то ? ‹ 0; он характеризует абсолютное уменьшение уровня.

Абсолютный прирост за единицу времени (месяц, год) измеряет абсолютную скорость роста (или снижения) уровня. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных приростов равна соответствующему базисному приросту, т. е. общему приросту за весь период.

Более полную характеристику роста можно получить только тогда, когда абсолютные величины дополняются относительными. Относительными показателями динамики являются темпы роста и темпы прироста, характеризующие интенсивность процесса роста.

Темп роста (Тр) – статистический показатель, который отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень; измеряется отношением текущего уровня к предыдущему или базисному:

Как и другие относительные величины, темп роста может быть выражен не только в форме коэффициента (простого отношения уровней), но и в процентах. Как и абсолютные приросты, темпы роста для любых рядов динамики сами по себе являются интервальными показателями, т. е. характеризуют тот или иной промежуток (интервал) времени.

Между цепными и базисными темпами роста, выраженными в форме коэффициентов, существует определенная взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста за весь соответствующий период, например: y2/ y1 y3/ y2 = y3/ y1.

Темп прироста (Тпр) характеризует относительную величину прироста, т. е. представляет собой отношение абсолютного прироста к предыдущему или базисному уровню: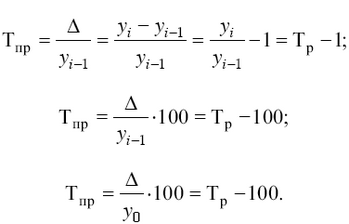

Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился (или уменьшился) уровень по сравнению с базисным, принятым за 100 %.

При анализе темпов развития никогда не следует упускать из виду, какие абсолютные величины – уровни и абсолютные приросты – скрываются за темпами роста и прироста. Нужно, в частности, иметь в виду, что при снижении (замедлении) темпов роста и прироста абсолютный прирост может возрастать.

В связи с этим важно изучать еще один показатель динамики – абсолютное значение (содержание) 1 % прироста, который определяется как результат деления абсолютного прироста на соответствующий темп прироста: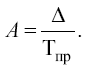

Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста. Иногда уровни явления за одни годы несопоставимы с уровнями за другие годы из-за территориальных, ведомственных и иных изменений (изменения методологии учета и исчисления показателей и т. п.). Чтобы обеспечить сопоставимость и получить пригодный для анализа временной ряд, нужно произвести прямой пересчет уровней, несопоставимых с другими. Однако иногда нет необходимых для этого данных. В таких случаях можно использовать особый прием, называемый смыканием рядов динамики.

Пусть, например, произошло изменение границ территории, по которой изучалась динамика развития какого-то явления в i-м году. Тогда данные, полученные до этого года, окажутся несопоставимы с данными за последующие годы. Чтобы сомкнуть эти ряды и получить возможность анализа динамики ряда за весь период, примем в каждом из них за базу сравнения уровень i-го года, за который есть данные как в прежних, так и в новых границах территории. Эти два ряда с одинаковой базой сравнения можно затем заменить одним сомкнутым рядом динамики. По данным сомкнутого ряда можно вычислить темпы роста по сравнению с любым годом, можно рассчитать и абсолютные уровни за весь период в новых границах. Тем не менее надо иметь в виду, что результаты, полученные путем смыкания рядов динамики, содержат в себе некоторую погрешность.

Графически динамика явлений наиболее часто изображается в виде столбиковых и линейных диаграмм. Применяются и другие формы диаграмм: фигурные, квадратные, секторные и т. п. Аналитические графики обычно строятся в виде линейных диаграмм.

С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития, поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и закономерностей и решения других задач анализа используются средние показатели временного ряда – средние уровни, средние абсолютные приросты и средние темпы динамики.

К расчету средних уровней ряда динамики часто приходится прибегать уже при построении временного ряда – для обеспечения сопоставимости числителя и знаменателя при расчете средних и относительных величин. Пусть, например, нужно построить ряд динамики производства электроэнергии на душу населения в Российской Федерации. Для этого за каждый год необходимо количество произведенной электроэнергии в данном году (интервальный показатель) разделить на численность населения в том же году (момент-ный показатель, величина которого непрерывно меняется на протяжении года). Ясно, что численность населения на тот или иной момент времени в общем случае несопоставима с объемом производства за весь год в целом. Для обеспечения сопоставимости нужно и численность населения как-то приурочить ко всему году, а это можно сделать, лишь рассчитав среднюю численность населения за год.

Часто приходится прибегать к средним показателям динамики и потому, что уровни многих явлений сильно колеблются от периода к периоду, например от года к году, то повышаясь, то понижаясь. Особенно это относится ко многим показателям сельского хозяйства, где год на год не приходится, поэтому при анализе развития сельского хозяйства чаще оперируют не годовыми показателями, а более типичными и устойчивыми среднегодовыми показателями за несколько лет.

При вычислении средних показателей динамики необходимо иметь в виду, что к этим средним показателям полностью относятся общие положения теории средних величин. Это означает прежде всего, что динамическая средняя будет типичной, если она характеризует период с однородными, более или менее стабильными условиями развития явления. Выделение таких периодов – этапов развития – в определенном отношении аналогично группировке. Если же динамическая средняя величина исчислена за период, в течение которого условия развития явления существенно менялись, т. е. период, охватывающий разные этапы развития явления, то такой средней величиной нужно пользоваться с большой осторожностью, дополняя ее средними величинами за отдельные этапы.

Средние показатели динамики должны также удовлетворять логико-математическому требованию, согласно которому при замене средней величиной тех фактических величин, из которых получена средняя, не должна изменяться величина определяющего показателя, т. е. некоторого обобщающего показателя, связанного с осредняемым показателем. Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежащего в основе ряда, т. е. от вида временного ряда.

Наиболее просто вычисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической: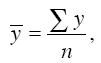

где n – число фактических уровней за последовательные равные отрезки времени.

Сложнее обстоит дело с вычислением среднего уровня моментного ряда динамики абсолютных величин. Момент-ный показатель может изменяться почти непрерывно, поэтому чем более подробны и исчерпывающи данные о его изменении, тем более точно можно вычислить средний уровень. Более того, сам метод расчета зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи.

При наличии исчерпывающих данных об изменении мо-ментного показателя его средний уровень вычисляется по формуле средней арифметической взвешенной для интервального ряда с разностоящими уровнями:

где t – число периодов времени, в течение которых уровень не изменялся.

Если промежутки времени между соседними датами равны друг другу, т. е. когда мы имеем дело с равными (или примерно равными) интервалами между датами (например, когда известны уровни на начало каждого месяца или квартала, года), тогда для моментного ряда с равностоящими уровнями расчет среднего уровня ряда производим по формуле средней хронологической: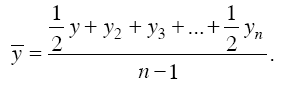

Для моментного ряда с разностоящими уровнями расчет среднего уровня ряда производится по формуле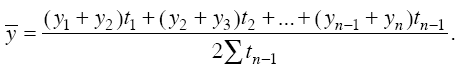

Выше шла речь о среднем уровне рядов динамики абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно вычислять исходя из содержания и смысла этих средних и относительных показателей.

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежемесячно, ежегодно и т. д.). Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:

• расчет среднего абсолютного цепного прироста: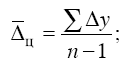

• расчет среднего абсолютного базисного прироста:

где – цепные абсолютные приросты за последовательные промежутки времени; n – число цепных приростов; У0 – уровень базисного периода.

В качестве основы и критерия правильности исчисления среднего темпа роста (как и среднего абсолютного прироста) можно использовать в роли определяющего показателя произведение цепныгх темпов роста, которое равно темпу роста за весь рассматриваемый период. Таким образом, перемножив n цепных темпов роста, мы получим темп роста за весь период: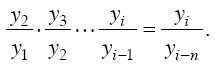

Поставим задачу найти такой средний темп роста (р), чтобы при замене им фактических цепных темпов в формуле 8.11 остался без изменения темп роста за весь период (у1 / у1 -1). Следовательно, должно соблюдаться равенство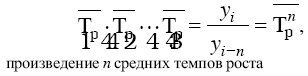

из которого следует: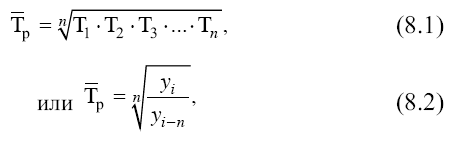

где n – число уровней ряда динамики; Т1, Т2, Тп – цепные темпы роста.

Формула (8.1) носит название простой средней геометрической, (8.2) – средней геометрической в неявном виде.

Средний темп роста, выраженный в форме коэффициента, показыгвает, во сколько раз увеличивается уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.).

Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:

Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.). Средний темп прироста характеризует среднюю интенсивность роста, т. е. среднюю относительную скорость изменения уровня.

Из двух видов формулы среднего темпа роста чаще используется формула (8.2), так как она не требует вычисления всех цепных темпов роста. По формуле (8.1) расчет целесообразно производить лишь в тех случаях, когда неизвестны ни уровни ряда динамики, ни темп роста за весь период, а известны только цепные темпы роста (или прироста).

Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. Для этого необходимо выделить такие периоды (этапы) развития, которые достаточно однородны в отношении взаимосвязи данного явления с другими и условий его развития.

Выделение этапов развития – это задача, находящаяся на стыке науки, изучающей данное явление (экономики, социологии и т. п.), и статистики. Решение этой задачи осуществляется не только и даже не столько с помощью статистических методов (хотя и они могут принести определенную пользу), сколько на базе содержательного анализа сущности, природы явления и общих законов его развития.

Для каждого этапа развития нужно выявить и численно охарактеризовать основную тенденцию изменения уровня явления. Под тенденцией понимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Если уровень непрерывно растет или непрерывно снижается, то тенденция к росту или снижению наблюдается отчетливо: она легко обнаруживается визуально по графику временного ряда. Следует, однако, иметь в виду, что и рост, и снижение уровня могут происходить по-разному: либо равномерно, либо ускоренно, либо замедленно. Под равномерным ростом (или снижением) понимается рост (или снижение) с постоянной абсолютной скоростью, когда цепные абсолютные приросты (;) одинаковы. При ускоренном росте или снижении цепные приросты систематически увеличиваются по абсолютной величине, а при замедленном росте или снижении – уменьшаются (тоже по модулю). Практически уровни ряда динамики очень редко растут (или снижаются) строго равномерно. Нечасто встречается и систематическое, без единого отклонения, увеличение или снижение цепных приростов.

Такие отклонения объясняются либо изменением с течением времени всего комплекса основных причин и факторов, от которых зависит уровень явления, либо изменением направления и силы действия второстепенных, в том числе случайных, обстоятельств и факторов, поэтому при анализе динамики идет речь не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении данного этапа развития. В некоторых случаях эта закономерность, общая тенденция развития объекта вполне четко отображаются уровнями динамического ряда.

Основной тенденцией (трендом) называется достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. Выявление основной тенденции развития (тренда) называется в статистике также выравниваем временного ряда, а методы выявления основной тенденции – методами выравнивания.

Одними из самых распространенных способов выявления основных тенденций (тренда) ряда динамики являются методы:

• укрупнения интервалов;

• скользящей средней (суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды). Расчет средних ведется способом скольжения, т. е. постепенным исключением из принятого периода первого уровня и включение следующего;

• аналитического выравнивания. При этом уровни ряда динамики выражаются в виде функций времени:

1) f (t) = a0 + a1t – линейная зависимость;

2) f (t) = a0 + a1t + a2t2– параболическая зависимость. Способ укрупнения интервалов и их характеристики средними уровнями заключается в переходе от интервалов менее продолжительных к более продолжительным, например от суток – к неделям или декадам, от декад – к месяцам, от месяцев – к кварталам или годам, от годовых интервалов – к многолетним. Если уровни ряда динамики колеблются с более или менее определенной периодичностью (волнообразно), то укрупненный интервал целесообразно взять равным периоду колебаний (длине «волны» цикла). Если же такая периодичность отсутствует, то укрупнение производят постепенно от малых интервалов к все более крупным, пока общее направление тренда не станет достаточно отчетливым.

Если ряд динамики является моментным, а также в тех случаях, когда уровень ряда является относительной или средней величиной, суммирование уровней не имеет смысла, и следует охарактеризовать укрупненные периоды средними уровнями.

При укрупнении интервалов число членов динамического ряда сильно сокращается, в результате чего движение уровня внутри укрупненного интервала выпадает из поля зрения. В связи с этим для выявления основной тенденции и более детальной ее характеристики используется сглаживание ряда с помощью скользящей средней.

Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее, начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.

Каждое звено скользящей средней – это средний уровень за соответствующий период. При графическом изображении и при некоторых расчетах каждое звено принято условно относить к центральному интервалу того периода, за который сделан расчет (для моментального ряда – к центральной дате).

Вопрос о том, за какой период следует вычислять звенья скользящей средней, решается в зависимости от конкретных особенностей динамики. Как и при укрупнении интервалов, если в колебаниях уровня есть определенная периодичность, то период сглаживания целесообразно принять равным периоду колебаний или кратной его величине. Так, при наличии квартальных уровней, испытывающих ежегодно сезонные спады и повышения, целесообразно применять четырех– или восьмиквартальную среднюю и т. п. Если же колебания уровней являются беспорядочными, то целесообразно постепенно укрупнять интервал сглаживания, пока не выявится отчетливая картина тренда.

Аналитическое выравнивание ряда динамики позволяет получить аналитическую модель тренда. Оно производится следующим образом.

• На основе содержательного анализа выделяется этап развития и устанавливается характер динамики на этом этапе.

• Исходя из предположения о той или иной закономерности роста и из характера динамики выбирается форма аналитического выражения тренда, вид аппроксимирующей функции, которой графически соответствует определенная линия: прямая, парабола, показательная кривая и т. п. Эта линия (функция) выражает предполагаемую закономерность плавного изменения уровня во времени, т. е. основную тенденцию. При этом каждый уровень ряда динамики условно рассматривается как сумма двух составляющих (компонент): yt=f(t)+?t. Одна из них (yt = f (t)), выражающая тренд, характеризует влияние постоянно действующих, основных факторов и называется систематический регулярной компонентой. Другая составляющая (8t) отражает влияние случайных факторов и обстоятельств и называется случайной компонентой. Эту компоненту называют также остаточной (или просто остатком), так как она равна отклонению фактического уровня от тренда. Таким образом, допускается (условно предполагается), что основная тенденция (тренд) формируется под влиянием постоянно действующих главных факторов, а второстепенные, случайные факторы вызывают отклонение уровня от тренда.

Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области. Наиболее простой эмпирический прием – визуальный: выбор формы тренда на основе графического изображения ряда – ломаной линии. На практике линейная зависимость используется чаще, чем параболическая, в силу ее простоты.