Глава 13: Внеземная мудрость: Геометрия, вибрация и более высокие измерения

К настоящему моменту следует быть более чем готовыми к полному раскрытию значения и важности геометрии Платоновых Тел для понимания многомерных свойств “единиц сознания”, какими мы их наблюдали на Земле. Термин “единица сознания” (ЕС) означает: энергетический сознательный “эфир” или энергия нулевой точки просачивается в физическое пространство и время, принимая форму светящейся сферы электромагнитной энергии с отверстием в середине, формирующим ось вращения север-юг. Их двух последних глав мы узнали, что такие сферические энергетические образования обладают геометрическими вихрями. Эта информация приходит из научных исследований поведения планет и математического анализа углов “тетраэдра” и отношений между различными объектами, расположенными в области Сидония на Марсе, имеющими, как полагают, искусственное происхождение.

Обычно считают, что прямолинейные структуры присущи только искусственным объектам и не являются частью природы. Поэтому бОльшая часть информации этой главы будет очень специфической. Мы никогда не пытались внушить, что любая планета обладает внутри себя гигантскими физическими кристаллами, наоборот, мы настаивали на том, что такая форма создается энергией, текущей в ЕС, и формирует планету. Мы не привыкли думать, что в своей вибрации звук или цвет обладают скрытыми геометрическими формами, и все же, именно к такому выводу подводит наше исследование.

В последних двух главах мы убедились в том, что все планеты демонстрируют признаки восхождения энергии в конкретных геометрических точках, определяемых такими формами как икосаэдр, додекаэдр и тетраэдр. Энергетические потоки, втекающие и вытекающие из полюсов в виде двух полей, вращающихся в противоположных направлениях, соединяются для формирования геометрических паттернов на поверхности планеты. (Как и почему они соединяются, мы обсудим в последующих главах.) Внутри планет существуют ядра из светящегося вещества, похожего на вещество Солнца, и проблемы модели динамо активно взывают к лучшему решению. Возвращаясь к обсуждению самих геометрий, мы видели, что они могут оказывать мощное влияние, как на “вибрационное состояние” физической материи, так и на условия пространства и времени. Короче говоря, представляется, что:

В точках геометрических узлов находятся “межпространственные” вихри энергии.

Мы уже говорили о том, что “более высокие измерения” пребывают вокруг нас, просто энергия в них вибрирует на более высокой частоте, чем уровень нашего фокуса. Сейчас, когда мы убедились в том, что геометрия тетраэдра, икосаэдра и других форм присуща всей Солнечной Системе, следует ожидать, что все планеты одним и тем же способом создаются гравитационными и межпространственными вихрями пространства и времени.

Интересно, что в книгах серии Закона Одного, переданных в 1981 году инопланетной группой, известной как Ра, предоставляется очень конкретная информация о понимании вибрации как ключевой “упущенной связи” для понимания более высоких измерений. Им не нравится слово “измерение”, они предпочитают пользоваться словом “плотность”. Это означает, что разные измерения — это разные плотности Одного Единого Эфирного Энергетического Источника, о котором мы уже писали в этой книге. Первая цитата рассматривает плотности как вибрации звука, вторая — как вибрации цвета.

Ра: Термин “плотность” — это то, что математически вы называете единицей. Если хотите, самая тесная аналогия обнаруживается в музыке, где у западной музыкальной шкалы имеется семь нот, а восьмая нота начинает новую октаву.

Ра: Природа вибрации такова, что ее можно считать имеющей математически прямые или узкие ступени. Эти ступени можно рассматривать как имеющие границы. Внутри каждой границы существует бесконечное число градаций вибрации или цвета. Однако при приближении к границе следует совершить усилие для ее пересечения. Цвета — самый простой способ выражения пограничных перегородок вашей плотности. (Книга 2, стр. 42)

Из нижеследующих цитат Ра можно видеть, что они осведомлены о геометрических энергиях, наблюдаемых на планетах, в сочетании с идеей о том, что более высокие измерения связаны с вибрацией жидкообразной среды:

Ра: Если хотите, представляйте многочисленные силовые поля Земли в виде геометрически точной паутины. Энергии втекают в то, что вы бы назвали планами Земли, из магнетически определенных точек. (Книга 1, стр. 81–82.)

Ра: Сотворяющая свет Любовь превращается в потоки любви/света в планетарной сфере, в соответствии с точками электромагнитной паутины или звеньями входа. Далее эти потоки поступают в распоряжении индивидуума, который, как и планета, представляет собой паутину электромагнитных энергетических полей с точками или звеньями входа.

Цитаты из книги Джейн Робертс Говорит Сетх, написанной на основе ченнелинговых сеансов в 1969 году, тоже четко указывают на вершины геометрических объектов как на межпространственные “точки потока” и еще больше детализируют высказывания Ра:

“В “пространстве” вашего мира существуют и другие формы реальности. Вы не воспринимаете их, а они, вообще говоря, не чувствуют вас. Это общее утверждение того, что разные точки ваших реальностей могут совмещаться и реально совмещаются.

Эти точки не осознаются как таковые, но являются точками, которые вы назвали бы двойной реальностью. У двойной реальности существуют точки пересечения. Координатные точки, в которых сливаются реальности, обладают огромным энергетическим потенциалом. Чисто математически, есть основные координатные точки, наделенные фантастической по интенсивности энергией, и множество второстепенных”.

[Примечание: “Математически безупречные” точки, о которых говорит Сетх, — на самом деле вершины Платоновых геометрий, которые мы обсуждали. А слияние реальностей четко прослеживается в Бермудском Треугольнике. Возможно, Сетх имеет в виду, что для сотворения вихревых качеств в этих точках сливаются два разных поля, отсюда использование слова “двойной”.]

(Долгая пауза в 9:29) Существуют четыре абсолютные точки пересечения всех реальностей.

[Примечание: Единственное Платоново Тело, обладающее четырьмя вершинами, — тетраэдр. Цитата Сетха утверждает, что тетраэдр почему-то важнее всех других геометрий. Хоагленд тоже верит в это, основываясь на Послании Сидонии. Позже мы увидим, почему это так.]

Также, они служат энергетическими каналами и искривлениями, сквозь которые возможен переход в другие реальности. Эти точки трансформируют энергию и предоставляют бо льшую часть порождающей энергии, обеспечивая непрерывность созидательного процесса (в ваших терминах). (Много пауз)

[Примечание: Как показали труды Ричарда С. Пасичника и Миссии Энтерпрайз, вершины тетраэдра являются источником огромных энергетических восхождений на планетах, таких как Огромное Красное Пятно на Юпитере. И вновь, вершины икосаэдра на Земле четко демонстрируют искривления из одной реальности в другую. Как правило, когда в речевых паттернах Джейн как Сетха много пауз, это означает, что она погружается в более глубокий уровень транса, чтобы донести информацию.]

В вашей реальности есть масса второстепенных точек. И как вы увидите позже, они играют важную роль в превращении мыслей и эмоций в физическую материю. Когда мысль или эмоция обретает определенную интенсивность, она автоматически притягивает энергию одной из второстепенных точек, интенсивно заряжается и намагничивается, хотя и не увеличивается в размерах.

Эти точки находятся и во времени, и в пространстве. Следовательно, существуют определенные точки пространства и времени (вновь в ваших терминах), более благоприятные, чем другие, в которых идеи и материя обретают более высокий заряд. Практически, это значит, что в менее благоприятных точках материализация займет больше времени (в вашем контексте), а в более благоприятных точках сочетание идей и формы будет относительно вечным. Например, пирамиды — именно такой случай.

[Примечание: Сейчас это может сбивать с толку, но позже мы убедимся, что эти геометрии влияют и на время, о чем и говорит Сетх. Слова Сетха о том, что в этих точках материя становится прочнее, совпадают с нашими наблюдениями того, что материя намного более гибкая, чем мы о ней думали. При определенных обстоятельствах, таких как торнадо, материя может сдвигаться по фазе и становиться менее твердой. Сейчас Сетх говорит о том, что те же самые силы, только в менее хаотической форме, могут укреплять материю.]

(Медленно в 9:43) Эти координатные точки — абсолютные, основные и второстепенные — представляют собой скопления или признаки чистой энергии. Если думать в терминах величины, они бесконечно малы, меньше, чем любая частица, известная вашим ученым, но состоят из чистой энергии. И все же эту энергию можно активировать. До тех пор она спит и не может быть активирована физически.

[Примечание: Именно это мы обнаружим в третьей книге: на мельчайших субатомных уровнях, геометрия — скрытый ключ к “чистой энергии” эфира.]

(9:50) А сейчас несколько подсказок, которые могли бы помочь вам или математикам. В окрестностях основных и даже второстепенных точек, гравитация и прочие так называемые физические законы будут нестабильны. Второстепенные точки также служат опорами для усиления структуры внутри невидимого полотна энергии, формирующего все реальности и проявления. Поскольку они являются признаками или скоплениями чистой энергии, во второстепенных точках существует большая разница в количестве доступной энергии, точно такая же разница прослеживается между основными и абсолютными точками”. [42] (Сеанс 524)

[Примечание: Это предсказание относится к Вихрю Орегона, который, бесспорно, является областью такого энергетического заряда. Гравитация в нем вызывает заметное изменение внутри вихря, влияет на ход времени и размеры физических объектов.]

Отсюда, полученная от инопланетян информация говорит о том, в местах, таких как двенадцать вихрей икосаэдра Сандерсона, жидкообразный вибрирующий эфир истекает в нашу реальность с более высоким уровнем плотности, чем окружающая привычная энергия. И поскольку эта энергия обладает более высокой “плотностью”, она будет преобразовывать в более высокую плотность всю окружающую ее материю, включая человеческую жизнь. Здесь у нас есть очень удачное новое объяснение явлений, которые мы уже исследовали.

Идея Ра, что “более высокие измерения” являются частью Октавы плотностей, реально обретает смысл и отвечает на многие парадоксы науки. Тогда, все, что нужно сделать, — это понять, что во всей Вселенной существует один единый “эфир”, который для дифференциации себя следует паттернам музыки и вибрации. Это исчерпывающе объясняет многие давно существующие загадки, и мы будем исследовать это в следующей главе. Сетх тоже освещает это положение:

“Что бы ни появилось в физических условиях, существует и в других условиях, которые вы не воспринимаете. Вы воспринимаете реальности только тогда, когда они достигают определенной “высоты тона”, когда они сливаются с материей. Но они существуют и действуют и на других уровнях”. (Сеанс 530)

[Примечание: Отметьте использование выражения “высота тона”. Это не просто метафора, это очень точное утверждение о Гармонической Вселенной и ее функционировании в виде эфирных энергетических плотностей.]

Поэтому ваша реальность не является системой реальности, сформированной са мой интенсивной концентрацией энергии. Просто это та реальность, на которую вы настроены, неотъемлемая часть Всего, Что Есть. И именно по этой причине вы ее воспринимаете.

Другие части вас, которые вы сознательно не осознаете, обитают в том месте, которое вы бы назвали суперсистемой реальности. В ней сознание учится справляться и воспринимать более сильные концентрации энергии и создавать “формы” другой природы” (сеанс 530)

И еще одна цитата:

“Вы знаете, что есть спектры света. Точно так же, есть и спектры материи. В сравнении с некоторыми другими системами реальности, ваша реальность не столь уж плотна. Ваши измерения физической материи лишь слегка намекают на все разнообразие (возможных) измерений”. (Сеанс 567) (Стр.77)

Итак, вновь имеется аналогия “спектров” измерений, существующих в структуре Октавы. Будучи сформирована из эфира, сама материя должна подвергаться изменяющимся уровням вибрации эфира, то есть, потенциально быть способной двигаться из одной реальности в другую. Это могло бы объяснить, почему торнадо может сплавлять твердые объекты, и почему в вихрях икосаэдра Земли происходят исчезновения. Кроме того, и Сетх и Ра настаивают на том, что наше сознание — ключевое звено, соединяющее нас со всеми другими уровнями реальности. На самом деле, мы — многомерные существа, утерявшие осознание “большой картины”.

Если иметь это в виду, тогда исследование свойств света, звука и геометрических вибраций, и как они работают вместе, заслуживает нашего обсуждения. Это будет общий материал, но очень важно иметь этот материал даже в такой форме прежде, чем мы продолжим обсуждение измерений в следующей главе. И Сетх и Ра настаивают на том, что необходимо более подробно исследовать эти взаимосвязанные свойства вибрации, чтобы обнаружить самые глубокие ответы.

Самый легкий и знакомый способ познакомиться с вибрацией — посредством звука. Любой музыкант скажет, что все вибрации звука сгруппированы в октавы. А мы знаем, что слово “окт” означает число восемь. В октаве существуют семь основных “узлов” вибрации, за ними следует восьмой. Восьмая нота играет двоякую роль, она не только завершает одну октаву, но и начинает новую.

Греческий математик и философ Пифагор, посредством процесса последовательного деления частоты на пять, впервые разработал восемь “чистых” тонов октавы, известных как диатоническая шкала. Он взял однострунный “монохорд” [43], и измерил точные длины волны при проигрывании разных нот.

Земной монохорд с его пропорциями и интервалами

Играя как на гитаре и двигаясь сверху вниз, он прижимал палец на различных длинах струны, и бренчал, чтобы получить разные ноты. Каждая проигранная нота делила струну на две разные части, затем для каждой ноты измерялись и записывались длины разных частей струны. Пифагор показал, что частоту (или скорость вибрации) каждой ноты можно представить в виде отношения между двумя частями струны, или двумя числами, отсюда термин “диатонические отношения”. Дальнейшее исследования деления на пять привели к созданию Октавы как самому простому группированию различных отношений, таких как 1:1, 2:1, 3:2, 5:3, 13:8 и 23:13.

Диатоническую шкалу можно видеть на пианино как белые клавиши, где первая нота октавы — до. У пианино есть еще и черные клавиши, и если включить и их, то получается Октава из тринадцати нот, где тринадцатая нота является началом следующей октавы. Тринадцать нот известны как хроматическая шкала, и бОльшая часть музыки всего мира будет состоять только из нот октавы. Поэтому все песни можно играть на пианино. (Как исключение: Индийская музыка пользуется нотами, не укладывающимися в хроматическую шкалу, их называют квотертонами или микротонами).

Математика считает, что основная причина выбора восьми нот вместо тринадцати “для группирования музыкальных нот октавы” в том, что все восемь “диатонических” нот будут приятно звучать вместе; иными словами, они будут гармоничны. Вы можете играть песню на белых клавишах пианино, и она всегда будет звучать как музыка, не зависимо от того, какие ноты вы берете. Однако если вы экспериментируете с хроматической шкалой, не зная, что делаете, вы получите болезненный диссонанс, и любой, находящийся в комнате, очень быстро попросит вас прекратить.

Математически, самая высокая нота в Октаве обладает скоростью вибрации или частотой вдвое большей, чем самая низкая нота. И это самый основной способ убедиться, что Октава образует одну полную группу звуковых вибраций.

Каждая нота, будь то ля, си, до, ре, фа, ми или соль, будет дублироваться в следующей октаве. Поскольку октавы постоянно дублируются, полоса частот, воспринимаемая человеческим слухом, ограничивается определенным числом октав. Выше определенного уровня, вибрации станут настолько быстрыми, что перестанут восприниматься человеческим ухом, хотя и будут существовать вокруг нас.

Итак, как из алфавита можно составить все возможные слова нашего языка, так и структура октавы содержит все возможные вибрации звука и раскрывает простой способ, как они сочетаются вместе. Теория Хаоса могла бы назвать Октаву “аттрактором”, что означает: все вибрации звука, как бы “хаотично” или случайно они не связывались друг с другом, могут “притягиваться” в структуру Октавы. Но вы можете спросить: “ Как насчет других немузыкальных звуков, таких как ветер?” Как звук ветра может увязываться с Октавой музыкальных нот? “Белый шум” — технический термин, обозначающий высокоскоростные, случайно рассеянные колебания звуковой частоты, не производящие любого отдельного тона, а создающие шипящий шум, который можно слышать, когда воздух выходит из шины. Хотя в этом звуке могут присутствовать тысячи перекрывающихся частот, мы знаем: если их надлежащим образом отделить друг от друга, каждая из них должна автоматически превращаться в часть октавы, на том или иной уровне. Просто когда слишком много разных звуков звучат слишком быстро, наше ухо не может отличить их друг от друга.

С научной точки зрения, звук — не более чем вибрация молекул воздуха. Математически, мы меряем звуки в терминах того, сколько раз воздух вибрирует в секунду времени. Это дает математическую величину, и любой, кто когда-нибудь играл на струнном инструменте, знает, что средний настроечный камертон покажет: нота ля — это 440 колебаний воздуха в секунду. Разная нота будет иметь разную величину колебаний в секунду, поэтому 440 колебаний в секунду будут всегда давать ноту ля. И это все, что есть. Позже мы убедимся, что, что эти “гармонические” числовые величины чрезвычайно важны для измерения и анализа поведения эфира.

Диатоническая числовая шкала частот

(Примечание: немного подогнано — объяснение позже)

Поскольку вы не пребываете в полном вакууме, плотность или состав вибрирующего воздуха значения не имеют, то есть, музыкальный инструмент будет звучать одинаково на вершине горы Эверест, где воздух разряжен, и на уровне моря, где воздух намного плотнее. Однако если сам воздух не имеет значения, тогда необходимо нечто другое, нечто, что вибрирует. Например, те же самые звуки мы можем слышать и под водой, такие как песни китов. Если ударить по металлу настроечного камертона, он может издать звук, и если держать основание камертона возле черепа, звук будет резонировать с вашим телом.

Таким образом, сама по себе среда не влияет на тон или высоту звука; вибрация может происходить в чистом воздухе, грязном воздухе, чистой воде, грязной воде, металле, плоти, кости или других формах, как в случае старомодного “телефона”, состоящего из двух оловянных банок, соединенных длинной струной. В этом случае, когда струна туго натянута между двумя банками, и один человек говорит в банку, а другой слушает, струна будет переносить звуковые вибрации, хотя, они и будут искажаться. Короче говоря, звуковые вибрации происходят не только в воздухе, они вибрируют во всем. Слышать звук — значит напрямую воспринимать и ощущать вибрации.

Хотя мы привыкли считать, что основные звуковые вибрации значимы и важны только для наших ушей, эта книга уже начала демонстрировать, что простые вибрации Октавы лежат в основе всей реальности, какой мы ее знаем. Невидимая “несжимаемая жидкость” эфира или “сознательная энергия”, формирующая Первичное Существо нашей Вселенной, может определенно представляться вибрирующей согласно этим принципам, что мы уже наблюдали на планетах. Именно поэтому индусы предложили идею, что АУМ является первичным звуком, сформировавшим Творение. И сейчас мы можем видеть, что звук строит Вселенную, а музыка — это способ физически услышать и ощутить суть самого Бога. Мы сами — творения Бога — состоим из живых, танцующих музыкальных волновых форм. Без музыки в своей жизни мы отвергаем само внутреннее знание и наслаждение своим существованием.

Идентичный уровень октавы вибраций содержится и в спектре видимого света. У нас есть белый свет, который с помощью призмы мы можем разложить на радугу из семи цветов — красный, оранжевый, желтый, зеленый, голубой, индиго и фиолетовый — прежде, чем начнется более высокий уровень октавы вибраций — инфракрасный и ультрафиолетовый. Сейчас мы знаем, что частота видимого света как пульсирующее “возбуждение” жидкообразной эфирной энергии — более высокая октава вибрации, чем частоты звука в музыкальной октаве. В целях упрощения, вы можете взять числовые отношения между каждой нотой музыкальной диатонической шкалы, удваивать их много раз, и со временем обнаружите те же отношения между скоростями вибрации светового спектра. Единственная разница между ними — величина; звук вибрирует намного медленнее, в то время как свет вибрирует намного быстрее.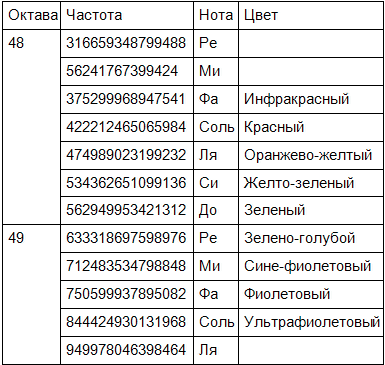

Из книги Дэйла Понда Физика любви: “Вышеприведенные отношения выведены из вычислений Пифагоровых частот и интервалов, начиная со слышимой полосы звука. Хотя существует много оттенков, скажем, зеленый цвет лежит в полосе от си до ре, на самом деле только нота до имеет 512 колебаний в секунду в более низкой слуховой октаве. Эти цвета имеют отношения к пигментам, а не к цветам света, которые были бы: до — красный, ре — оранжевый, ми — желтый, фа — зеленый, соль — голубой, ля — индиго и си — фиолетовый.

Когда любые частоты света или длины волны движутся в пространстве, они движутся с тем, что считается постоянной скоростью — грубо говоря, 300.000 км с секунду. Однако это наблюдение не рассматривает свет, как движущийся через эфирную среду с данной скоростью. Большинство людей уверено, что ничто во Вселенной не может превысить эту скорость. Поэтому скорость света или “с” — самое быстрое движение или вибрация, которую с нашей точки зрения мы обычно распознаем здесь на Земле, в третьем измерении. Как опубликовано в газете Нью-ЙоркТаймс в мае 2000 года, необычные условия в лаборатории, такие как трубка с цезием под высоким давлением, освещаемая светом, падающим “сбоку”, может создать скорость света в триста раз быстрее, чем “с”. По сути этот эксперимент идентичен экспериментам Бирдена со “скалярной волновой интерферометрией”.

Отсюда, если бы мы сгруппировали все возможные вибрации в таблицу, то получили бы полное отсутствие движения внизу таблицы, а скорость света — наверху. Скорость света определяет границу вибраций в нашей реальности. Вопреки положению Эйнштейна, объект, движущийся со скоростью света, не может создавать в материи бесконечную плотность; источники, такие как Ра, рассматривают скорость света как вершину вибраций в третьей плотности или измерении. Если мы двигаемся в область или “домен”, в котором эфир движется с более высокой скоростью, скорость света меняется, и материя естественно “фокусируется” в этом новом вибрационном уровне. Это подтверждается наблюдениями торнадо и других аномалий, а также аномалиями вихрей, демонстрирующих изменения пространства, времени и материи.

Самые первые слова Книги Бытия в Библии таковы: “В начале Бог сказал: “Да будет свет”, и стал свет”. Мы можем продемонстрировать, что все вибрации, сотворяющие нашу Вселенную, являются разными формами одной единой сознательной энергии. Без наблюдения ярко-красного, голубого, зеленого, желтого, фиолетового и оранжевого Света в повседневной жизни, мы отказываем себе во внутреннем знании и наслаждении своим существованием. Жизнь без цвета “скучная”, “серая”, “унылая” и “черная”.

Геометрия завершает основную триаду нашего восприятия фундаментальных строительных блоков вибрации во Вселенной — эта триада: свет, звук и геометрия. Наряду с геометрией, которую мы уже обсуждали, в физической форме вдруг появляются звуки музыки и цвета радуги. Внезапно, абстрактные концепции гармонии и цвета раскрывают структуры, состоящие из прямых и кривых линий, которые затем мы можем моделировать и строить вещи. Хотя мы можем видеть цвет и слышать звук, обычно мы не думаем о физической геометрической форме в двух или трех измерениях, которая будут точно представлять эти вибрации. Однако многие исследователи, такие как Джеральд Хокинс, Бакминстер Фуллер и Ганс Дженни, показали, что звуковые вибрации будут образовывать определенные геометрические паттерны. Также они доказали: мы видим то, что вибрирует, вместо воздуха, который обычно мы не видим.

На самом деле Джеральд Хокинс не совершил свои открытия, изучая вибрацию. В его случае, он пришел к своим выводам после многих лет исследования явления “кругов на полях”, когда сложные геометрические паттерны появляются буквально за одну ночь на различных полях всего мира. Обычно они видны только с воздуха. Изучив сотни такие образований, Хокинс осознал, что некоторые паттерны повторяются, и общность всех паттернов выражается простыми двумерными формами, такими как треугольник, квадрат и шестиугольник, совершенно вписанными в окружность так, что все вершины формы касаются окружности. К его изумлению, площадь поверхностей внутренних геометрий, будучи разделена на площадь внешних кругов, демонстрировала отношения, ответственные за вибрации музыки в Октаве, — “диатонические отношения”, о которых мы упоминали выше. Именно это показал Пифагор на однострунном “монохорде”, только вместо отношения длин струны, у нас есть отношение геометрии, указывающее на то же самое. Хокинс осознал, что это абсолютно новая и нераспознанная серия теорем в геометрии, и ни один ученый, с которым он консультировался, не знаком с этими концепциями. Итак, в двух измерениях мы можем понимать звук как “плоскую” геометрическую вибрацию (такую как треугольник), появляющуюся внутри “плоской” окружности.

Диатонические геометрические доказательства Хокинса

Хотя работа Хокинса выполнена в 1980-х годах и затрагивает только два измерения, эксперименты, проведенные студентами д-ра Бакминстера Фуллера, десятью годами раньше, впервые доказали, что звуковые вибрации трехмерны по своей структуре. Позднее, чтобы доказать этот эффект, студенты Фуллера использовали белый воздушный шар, помещенный в ванну с темными чернилами и вибрирующий на чистых диатонических звуковых частотах. Как и ожидалось, чернила собирались и окрашивали те области шара, которые подвергались самому меньшему количеству движения. Эти области оказались равномерно распределенными “узлами” или точками, где все искажающие движения на поверхности шара взаимно уничтожались до “нулевой зоны”, поэтому там могли легко накапливаться чернила. Более того, узлы связывались вместе не четкими и совершенно прямыми линиями чернил. То есть, звуки наблюдались как простые трехмерные геометрические формы, образующие линии, которые пересекались на самом шаре.

Октаэдр Звездный тетраэдр Куб Додекаэдр Икосаэдр

В экспериментах, вдохновленных Бакминстером Фуллером, “Платоновы” Тела раскрываются как звуковые вибрации.

Наблюдая эти формы, мы помним: все они идеально вписываются в сферу, а их вершины — впервые обнаруженные “узлы”. Также, важно помнить, что сфера является самой гармонической формой и образует внутри себя все другие геометрии.

Находками Фуллера и его студентов, что вибрации трехмерны, увлекся Ганс Дженни. Он искал способ доказать это более просто и менее громоздко, чем использование погруженного в чернила шара. В научном исследовании д-ра Дженни, известном как “Киматика”, он продемонстрировал геометрию звуковых вибраций, используя тонкие контейнеры, наполненные следующими средами: песком, спорами грибка Лигодеум, мокрым гипсом и разными формами жидкости, обладающими крошечными частицами или плавающими в них “коллоидами”. В этой книге особый интерес представляет коллоидная жидкость. Находясь в состоянии покоя, коллоиды равномерно распределяются в жидкости, и вода становится мутной. Д-р Дженни называет такое состояние “гидродинамическим рассеиванием”. Однако когда контейнер вибрировал на чистых диатонических звуках, частицы в жидкости собирались в упорядоченные и изолированные видимые геометрические паттерны, многие из которых обладали двумерной и трехмерной структурой. Иными словами, в них можно было наблюдать сформировавшуюся и ясно воспринимаемую глубину, то есть, они не были “плоскими. В этой книге, это одно из самых важных положений, которое следует изучить и помнить, ибо оно предоставляет неопровержимое, визуальное доказательство концепций, которые мы обсуждали.

Ганс Дженни: Пример звуковых вибраций в коллоидной воде

На рисунке можно видеть только пять основных трехмерных форм, и мы знаем их как Платоновы Тела, ибо честь их открытия принадлежит греческому философу Платону. Важно, чтобы было предельно ясно: наблюдая эти формы, на самом деле мы наблюдаем вибрацию. Сами формы могут не “существовать” как физический объект, а быть голограммой. Если вы попытаетесь их схватить или нарушить, они просто исчезнут и превратятся в рябь вокруг ваших пальцев. Тем не менее, не будучи нарушенными, формы будут существовать как очень реальная вибрация, и оказывать точно такое же давление на тело, которое вы ощущаете от очень громкого звука или раската грома. Сейчас, когда мы увидели формы вибраций, работающие в жидкообразном эфире, мы знаем, что созданные их давлением силовые линии позволяют по-новому взглянуть на динамику гравитации. Имея неопровержимые свидетельства того, как эти геометрии формируют структурные особенности поверхности Земли, такие как континенты, подводные хребты и горные образования, нас больше не ослепит истина. И только дело времени, когда простые наблюдения превратятся в общеизвестное знание основной массы человечества.

Также, очень важно упомянуть следующее: когда студенты Фуллера повышали частоту в шаре, или Дженни повышал частоту в воде, старые формы растворялись и исчезали, а на их месте появлялась более сложная геометрическая форма. Такое явление работало и наоборот: когда частота понижалась до первоначального значения, вновь появлялись геометрии той же самой формы. Поэтому, изучая динамику эфира, мы увидим: при повышении вибрационной частоты (или напряжения) энергии в данной области, сама геометрия этой области, например, формирующая Землю, будет спонтанно преобразовываться в более высокий порядок сложности. И эффекты повышения и понижения частоты происходят во всем Творении, включая все тела нашей Солнечной Системы, когда она двигается в Галактике. Работа д-ра Спилхауса продемонстрировала, что со времени первичного “мега-континента” Пангеи, гравитационное поле Земли уже прошло через несколько подобных преобразований. В то время Земля имела единую кору. Это было до движения расширения, которое сейчас рассматривается в Теории Глобального Тектонического Расширения, созданной в 1933 году Отто Хильгенбергом.

Итак, простые геометрические паттерны, формирующиеся вибрациями звука (и высокочастотными вибрациями света), можно рассматривать в двух и трех измерениях; причем двумерные формы, такие как треугольник, квадрат или шестиугольник, обсуждаемые Хокинсом, нам знакомы больше, чем трехмерные формы, открытые Фуллером и Дженни. Хотя к настоящему моменту мы уже наблюдали, как эти геометрии работают на планетах. Очень важно: вибрационные геометрии могут увеличиваться и уменьшаться в размерах, и эти простые движения организовываются и контролируются видимыми геометрическими структурами. Когда мы начинаем помещать формы одну в другую, они становятся “загнездованными”, причем каждая последующая форма гармонически растет и становится больше, чем предыдущая. По мере продолжения книги, мы расскажем об этом больше. Геометрия “сферы внутри сферы” уже наблюдалась в различных экспериментах, и сейчас следует ожидать, что внутри расширяющихся сфер существуют различные геометрические гармонии.

Самый простой способ смоделировать геометрическое расширение одной формы в другую — это проследить движение узлов относительно друг друга. Мы помним, что на Земле Спилхаус и другие назвали расширяющиеся геометрические движения “радиальными” или “спиралевидными”. Самый простой способ изобразить движение от узла к узлу между двумя различными формами — спиралевидная линия, которую Ра называет “спиралевидной линией света”. Такие спирали включают Спираль Фибоначчи или “Золотое Сечение” и спирали, образованные квадратными корнями из двух, трех и пяти. Сейчас с помощью математики мы продемонстрируем, что эти спирали напрямую связаны с музыкальными частотами.

Самое главное и самое важное из всех учений о спиралях известно как “Золотое Сечение”, Спираль Фибоначчи или спираль “фи”. Чтобы лучше понять эту спираль, мы начнем с гармонического вибрационного способа, который создается суммированием чисел. По существу, мы убедимся, что каждое новое число — это сумма двух предыдущих. Мы начинаем с единицы, прибавляем к ней единицу и получаем два. Затем мы берем два, складываем его с предыдущим числом, единицей, и получаем три. Затем мы берем три, складываем с предыдущим числом, два, и получаем пять. Продолжаем:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89….

Итак, числа продолжают возрастать простым гармоническим способом, где каждое новое число представляет собой сумму двух предыдущих. Если мы разделим пары чисел друг на друга, то на ранних стадиях увидим все общие диатонические музыкальные отношения, открытые Пифагором, такие как 3/2, 5/3, 8/5, 13/8 и 21/13. Это не должно удивлять, ибо музыка — это вибрационное движение, а техника суммирования, используемая в отношении фи, тоже является формой вибрации. Элегантная природа этой вибрации легко видна на рисунке “спирали фи”, приведенном ниже. Чтобы лучше понять, как спираль работает с Платоновыми Телами, ее следует рассматривать как трехмерный объект, как будто она наворачивается вокруг конуса с вершиной в точке G и нижней точкой А. Такой вид трехмерной спиралевидной формы называется “конической спиралью”.

Спираль Фибоначчи или “фи” и геометрические дополнения

Хотя на ранних этапах числовые серии “фи” будут образовывать между собой музыкальные отношения, по мере роста пары чисел, отношения между ними становятся все более и более одинаковыми, и процесс роста стабилизируется. По мере продолжения процесса, каждая пара чисел в серии будет делиться друг на друга и образовывать одно и то же число, а это значит, что отношение между всеми числами остается постоянным. Именно по этой причине само отношение называется “константой”, поскольку это всегда будет одно и то же число (и так до бесконечности), равное:

1,618033988749894484820….

Еще один интересный факт: мы можем начать с любых двух чисел, не смотря на их различие, и складывать их, используя простую приведенную выше формулу. Не смотря на то, какими разными они могут быть, через небольшой промежуток времени, мы снова получим отношение между ними, равное константе “фи”. Эта концепция вдохновила многие поколения математиков, музыкантов, ученых и философов, поскольку загадочно появляется под многими разными обличиями, включая пропорции роста растений, животных и человеческих существ. Как мы говорили, музыкальные отношения “фи” создают структуру простой геометрии в двух и трех измерениях, которая, как мы сейчас знаем, представляет собой форму вибрации. Это ясно показывает вышеприведенный рисунок, ибо, пока спираль продолжает расширяться, мы можем видеть шесть равнобедренных треугольников идентичных пропорций. Величина отношения между каждыми из двух треугольников будет константой “фи” или 1,618… приведенной выше.

Спирали показывают, как простые геометрические формы могут становиться все больше и больше или все меньше и меньше. В то время как спираль разворачивается или сворачивается, то же самое делают и геометрические формы, образовывающиеся внутри нее, — увеличиваются или уменьшаются. Иными словами, если спираль расширяется вовне, треугольники становятся больше. Если спираль сжимается вовнутрь, по направлению к точке F, треугольники становятся меньше.

Именно такой принцип спирали позволяет наличие простых расширяющихся паттернов роста в Природе, чтобы выражать себя, будь то в кристаллических структурах или живых организмах. Если бы мы могли изобразить геометрию того, как более простые геометрии сферического шара Фуллера расширялись в более сложные формы, когда он повышал вибрацию, мы бы увидели, что их расширения можно точно изобразить с помощью упомянутых выше простых гармонических спиралей.

Сферическое шестиренчатое расширение тетраэдральной формы, связанное с траекториями спирали, основанными на фракталах

Вышеприведенный рисунок появился на очень большом образовании “круга на полях”, названным “Тройная Серия Юлии”. В 1996 году оно появилось буквально за одну ночь на пшеничном поле в Англии. Это модель того, как выглядит система взаимосвязанных спиралей и Платоновой геометрии, расширенная в три измерения. Сам круг на полях состоял только из трех спиралей, образующих отдельные круги. А все прямые линии, внешняя сфера и экватор добавлены для того, чтобы лучше проиллюстрировать наблюдаемое. Это модель вибрации эфира, создающей видимые планетарные энергетические напряжения и четко измеряемые структуры времени. Сейчас следует визуализировать каждый треугольник как тетраэдр, обладающий своим сферическим полем и превращающий эту геометрическую схему в “матрешку” или сферу энергии “загнездованных кукол”, которую мы видели во многих экспериментах, таких как проведенных д-ром Чернобровом.

Итак, уже можно понять, почему древние рассматривали прямые и изогнутые линии как две противоположности во Вселенной, хотя на самом деле они являются единой вибрацией. Мы чувствуем, что согласно одному образу мышления, прямые линии и геометрии могут представлять собой пространство, а изогнутые линии и спирали — время. Но сейчас мы будем выражать это в более знакомых терминах и скажем, что прямые линии создают форму, а изогнутые — движение и рост этой формы. Иными словами, прямые линии формируют геометрические структуры самих вибраций, а изогнутые — пути для расширения и сжатия этих структурированных частот. Хотя обычно мы не думаем об изогнутой геометрии в связи со звуком и светом, мы знаем, что именно спирали управляют движением между одной нотой октавы и следующей более высокой нотой, или между одним цветом спектра и следующим более высоким цветом.

Попробуем выразить все вышесказанное в более духовном контексте. Во многих древних мистических традициях прямая линия считалась мужской силой и ассоциировалась с Солнцем, а изогнутая — женской силой и ассоциировалась с Луной. Мужские/женские энергии очень легко и интуитивно работают в наших умах. В состоянии покоя клетка спермы образует прямую линию, а яйцеклетка обладает круглой структурой. Тела мужчин по своему строению более тяжелые или прямолинейные, в то время как тела женщин — более плавные и округлые. Тенденция мужского ума — думать более линейно, жестко, посредством математических паттернов “левого полушария”, ум женщин более изогнутый, текучий, с эмоциональными паттернами “правого полушария”. Первобытные мужчины охотились и строили при свете Солнца, используя прямые копья и стрелы для добычи пищи, или позднее прямые доски, молотки и гвозди для строительства сооружений. Женщины готовили еду в плавных, круглых керамических или деревянных горшках, кормили детей плавной, округлой грудью в уединенной темноте пещеры, иглу или типи, укрываясь от дневного света, под которым когда-то бродили хищники и злодеи. Кроме того, женщины напрямую связаны с Луной так, как никогда не были связаны мужчины, — своим месячным циклом, демонстрируя еще один уровень, почему древние связывали женский дух с нашим Полуночным Солнцем.

Учение о различных геометрических формах и спиралях, включая их духовные связи с человечеством (как частично продемонстрировано выше), известно как “сакральная геометрия”.Одноименная книга Роберта Лолора — бесспорно, самая лучшая книга по этой теме. На протяжении истории многие великие ученые детально изучали принципы сакральной геометрии. Их потрясло открытие, что все разнообразные жизненные формы на Земле демонстрировали вибрационные принципы музыки, включая взаимодействие пространства и времени — прямые и изогнутые линии. Простые ракушки являются совершенным представлением спирали Фибоначчи, то же самое относится к паттерну роста растений, отпечаткам пальцев, рогам быка, внутренней части подсолнуха или лотоса, и многим-многим различным пропорциям в структурах скелета животных и человеческих существ. Очевидно, нет ограничений тому, как далеко будут заходить эти принципы, побуждая людей математически изучать каждое растение или организм по отдельности в поисках этих связей. Поскольку ученые не дают основания верить, что такие гармонические принципы необходимы для роста жизненных форм, тогда почему они существуют? Если бы эти пропорции не были важны, тогда почему мы все время их видим? А может, мы просто игнорируем существующее вокруг нас свидетельство — свидетельство, указывающее на то, что все во Вселенной — продукт вибрации? Если фундаментальная энергия, создающая всю реальность, вибрирует в гармоническом резонансе, может ли быть так, чтобы что-то не обладало гармонической основой?

Только что мы убедительно продемонстрировали, что спирали связывают воедино все Платоновы Тела. Чтобы подтвердить это положение, мы приводим таблицу из книги Сдвиг Эпох. Из книги Роберта Лолора Сакральная геометрия мы узнаем, что индусы сводили геометрии Платоновых Тел в структуру октавы, которую мы видим для звука и света. Нижеприведенная таблица перечисляет геометрию в определенном порядке. Это дает полную и законченную картину, как работают вместе различные вибрации, которые мы увидим в следующей главе. Сейчас достаточно знать, что такая таблица существует. Она основана на присвоении ребрам куба длины, равной “1”. Затем мы сравниваем с этой величиной ребра всех других форм, больше они или меньше. Мы помним, что в Платоновых Телах каждая грань имеет одинаковую форму, каждый угол идентичен, каждый узел находится на одинаковом расстоянии от всех других узлов, и каждая линия имеет одинаковую длину.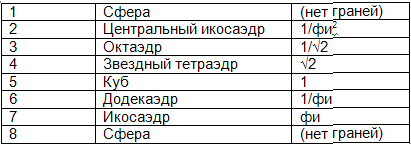

Гармонические пропорции Платоновых Тел

В следующей главе мы приведем бесспорный пример того, что древние индусы знали все и даже больше об энергетических полях, которые мы обсуждали. Нам повезло обнаружить редкую книгу Рамы Прасада, изданную в 1894 году и озаглавленную Тончайшие силы природы: Наука дыхания и философия таттв[44]. Мы увидим, что значение слова “таттва” аналогично значению нашего слова “вибрация”. Количество соответствий между тем, что мы уже наблюдали, и данными книги Прасада воистину потрясает, ибо почти каждый ключевой аспект эфирной модели, которую мы описали, содержится на страницах этой книги в той или иной форме. Также, мы посмотрим, как древняя эфирная концепция “октавы” измерений соотносится с современными научными учениями, и покажем, что примирить два мнения легче, чем мы думали. Кроме того, посредством осознания того, как геометрия пересекается с более высокими измерениями, что мы уже наблюдали на планетах, мы поймем, что идея “гиперпространственной физики” переходит из сферы умозаключений в область прикладной науки. И научившись применять эти концепции, мы откроем дверь во Вселенную.

Примечания:

4

4 http://www.disclosureproject.org

42

42 Говорит Сетх. Ченнелинг vi. К.: “София”, 1999. стр. 34-35

43

43 Монохорд — однострунный музыкальный инструмент, распространенный в Древней Греции и Риме, в Западной Европе до 19 века.

44

44 Сноска приводится в следующей главе