Перед программистом нередко возникает задача вычисления арифметических или иных выражений, не известных на этапе компиляции программы. Готовых средств для этого в Delphi нет. В Интернете можно найти компоненты и законченные примеры вычисления выражений, но нередко требуется создать что-то свое. В этой главе мы рассмотрим способы программного разбора и вычисления арифметических выражений. Кроме самих примеров будут изложены основы теории синтаксического анализа, с помощью которой эти примеры написаны. Эти сведения не только помогут лучше понять приведенные примеры, но и позволят легко написать код для синтаксического разбора любых выражений, которые подчиняются некоторому формальному описанию синтаксиса.

Синтаксический анализатор мы будем создавать поэтапно, переходя от простых примеров к сложным. Сначала научимся распознавать вещественное число и напишем простейший калькулятор, который умеет выполнять четыре действия арифметики над числами без учета приоритета операций. Затем наша программа научится учитывать приоритет этих операций, а чуть позже — использовать скобки для изменения этого приоритета. Далее калькулятор обретет способность работать с переменными, вычислять функции и возводить в степень, т.е. станет вполне полноценным. И на последнем этапе мы добавим лексический анализатор — средство, которое формализует разбор выражений со сложной грамматикой и тем самым существенно облегчает написание синтаксических анализаторов.

Прежде чем двигаться дальше, введем базовые определения. Языком мы будем называть множество строк (в большинстве случаев это будет бесконечное множество). Каждое выражение (в некоторых источниках вместо "выражение" употребляются термины "предложение" или "утверждение") может принадлежать или не принадлежать языку. Например, определим язык так: любая строка произвольной длины, состоящая из нулей и единиц. Тогда выражения "000101001" и "1111" принадлежат языку, а выражения "5х" и "R@8" — нет.

Синтаксисом называется набор правил, которые позволяют сделать заключение о том, принадлежит ли заданное выражение языку или нет.

С практической точки зрения наиболее интересны те языки, выражения которых не только подчиняются каким-либо синтаксическим правилам, но и несут смысловую нагрузку. Например, выражения языка Delphi — программы — приводят к выполнению компьютером тех или иных действий. В данном случае семантика языка Delphi — это правила, определяющие, к выполнению каких именно действий приведет то или иное выражение. В более общем смысле семантика языка — это описание смысла языковых выражений.

Другими словами, синтаксические правила позволяют понять, допустимо ли в выражении, принадлежащем заданному языку, появление в указанной позиции данного символа, а семантические — что означает появление этого символа в данной позиции.

Чтобы подчеркнуть разницу между синтаксисом и семантикой, рассмотрим такой оператор присваивания в Delphi:

X := Y + Z;

X

Таким образом, синтаксический анализ арифметических выражений — это всего лишь выяснение, корректно ли выражение. Мы же говорили о вычислении выражений, а это уже относится к семантике, т.е., строго говоря, мы здесь будем заниматься не только синтаксическим, но и семантическим анализом. С точки зрения теории синтаксический и семантический анализ разделены, т. е. анализировать семантику можно начинать "с нуля" после того, как анализ синтаксиса закончен. Но на практике легче объединить эти два процесса в один, чтобы пользоваться результатами синтаксического разбора при семантическом анализе. Из-за этого, как мы увидим в дальнейшем, иногда приходится вводить сложные синтаксические правила, которые в итоге описывают тот же язык, что и более простые, чтобы упростить семантический анализ.

На примере выражения

X := Y + Z;

Что касается семантики, то формальные правила ее описания отсутствуют. Поэтому семантика описывается словами, или же язык использует интуитивно понятную семантику. Например, арифметическое выражение "2+2" выглядит очень понятно в силу того, что мы к нему привыкли, хотя с точки зрения математики объяснить, что такое число и что такое операция сложения двух чисел, не так-то просто.

Кроме синтаксического и семантического анализа существует еще и лексический анализ — разделение выражения на отдельные лексемы. Лексемами называются последовательности символов языка, которые имеют смысл только как единое целое. Например, выражение "2+3" не относится к лексемам, т.к. его части — "2", "3" и "+" — имеют значение и вне выражения, а смысл всего выражения будет суперпозицией значений этих частей. А вот идентификатор

TForm

Для разбора простого синтаксиса нет нужды проводить отдельный лексический анализ, лексемы выделяются непосредственно при синтаксическом анализе. Поэтому большинство примеров, приведенных далее, будет обходиться без лексического анализатора.

Существует несколько различных (но, тем не менее, эквивалентных) способов описания синтаксиса. Мы здесь познакомимся только с самой употребляемой из них — расширенной формой Бэкуса-Наура. Эта форма была предложена Джоном Бэкусом и немного модифицирована Питером Науром, который использовал ее для описания синтаксиса языка Алгол. (Примечательно, что практически идентичная форма была независимо изобретена Ноамом Хомски для описания синтаксиса естественных языков.) В русскоязычной литературе форму Бэкуса-Наура обычно обозначают аббревиатурой БНФ (Бэкуса-Наура Форма). Несколько неестественный для русского языка порядок слов принят, чтобы сохранилось сходство с английской аббревиатурой BNF (Backus-Naur Form). Со временем в БНФ были добавлены новые правила описания синтаксиса, и эта форма получила название РБНФ — расширенная БНФ (далее для краткости мы не будем делать различия между БНФ и РБНФ). Совокупность правил, записанных в виде БНФ (или другом формализованным способом), называется грамматикой языка.

Основные понятия БНФ — терминальные и нетерминальные символы. Терминальные символы — это отдельные символы или их последовательности, являющиеся с точки зрения синтаксиса неразрывным целым, не сводимым к другим символам. Другими словами, терминальные символы — это лексемы. Терминальные символы могут состоять из одного или нескольких символов в обычном понимании этого слова. Примером терминальных символов, состоящих из нескольких символов, могут служить зарезервированные слова языка Паскаль и символы операций

>=

<=

<>.

Нетерминальный символ — это некоторая абстракция, которая по определенным правилам сводится к комбинации терминальных и/или других нетерминальных символов. Правила должны быть такими, чтобы существовала возможность выведения из них выражения, полностью состоящего из терминальных символов, за конечное число шагов, хотя рекурсивные определения терминальных символов друг через друга или через самих себя допускаются. Нетерминальные символы имеют имена, которые принято обрамлять угловыми скобками:

<Operator>

Операция

::=

<Separator> ::= '.'

В данном примере мы определили нетерминальный символ

<Separator>

<Separator>

В более сложных случаях нетерминальному символу ставится в соответствие не один символ, а их цепочка, в которую могут входить как терминальные, так и нетерминальные символы. Примером такого определения может служить описание синтаксиса оператора присваивания в Delphi:

<Assignment> ::=<Var> ':=' <Expression>

При записи синтаксиса в БНФ часто сначала дают определение абстракции самого верхнего уровня, описывающей все выражение в целом, и только потом — определения абстракций нижнего уровня, которые необходимы при ее определении, т.е. порядок определения абстракций может отличаться от принятого в языках программирования определения идентификаторов, согласно которому идентификатор должен быть сначала описан, и лишь затем использован. В частности, в данном примере символы

<Var>

<Expression>

<Assignment>

Операция

|

<Sign>

+

-

<Sign> ::= '+' | '-'

Если альтернатив больше, чем две, они записываются в ряд, разделенные символом

|

<Digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

Здесь мы определили нетерминальный символ <Digit> (цифра), под которым можем понимать один из символов диапазона

'0'..'9'

Операция

|

|

<for> ::= 'for' <Var> ':=' <Expression>

 ('to' | 'downto') <Expression> 'do' <Operator>

Здесь с помощью БНФ описан синтаксис оператора

for

<if> ::= 'if' <Condition> 'then' <Operator> ['else' <Operator>]

Здесь дано определение условного оператора

if

else

Примечание

Строго говоря, определения операторов

if

и

for

в Delphi сложнее, чем те, которые мы здесь привели. Это связано с тем, что

<if>

и

<for>

— это альтернативы символа

<Operator>

. Поэтому может возникнуть конструкция типа

if Condition1 then if Condition2 then Operator1 else Operator2

. Из нашего определения невозможно сделать вывод о том, к какому из двух

if

в данном случае относится

else

. В языках программирования принято, что

else

относится к последнему из

if

, который еще не имеет

else

. Чтобы описать это правило, требуется более сложный синтаксис, чем мы здесь привели. Однако этот вопрос выходит за рамки данной книги и более подробно рассмотрен в [5].

Фигурные скобки означают повторение того, что в них стоит, ноль или более раз. Например, целое число без знака записывается повторением несколько раз цифр, т.е. соответствующий нетерминальный символ можно определить так:

<Unsigned> ::= {<Digit>}

Это простое определение не совсем верно, т.к. фигурные скобки указывают на повторение ноль или большее число раз, т.е. пустая строка также будет соответствовать нашему определению

<Unsigned>

<Unsigned> ::= <Digit> {<Digit>}

Теперь синтаксическое правило, определяемое символом

<Unsigned>

В некоторых случаях после закрывающей фигурной скобки ставят символ "+" в верхнем индексе, чтобы показать, что содержимое скобок должно повторяться не менее одного раза. Например, следующее определение

<Unsigned>

<Unsigned> ::= {<Digit>}⁺

Однако это обозначение не является общепризнанным, поэтому мы не будем им пользоваться.

Этим исчерпывается набор правил БНФ. Далее мы будем использовать эти правила для описания различных синтаксических конструкций. При этом мы увидим, что, несмотря на простоту, БНФ позволяет описывать очень сложные конструкции, и это описание просто для понимания.

Попытаемся описать синтаксис вещественного числа с помощью БНФ. Сначала опишем этот синтаксис словами: "Перед числом может стоять знак — плюс или минус. Затем идет одна или несколько цифр. Потом может следовать точка, после которой будет еще одна или несколько цифр. Затем может быть указан показатель степени "Е" (большое или малое), после которого может стоять знак плюс или минус, а затем должна быть одна или несколько цифр". Указанные правила описывают синтаксис записи вещественных чисел, принятый в Delphi. Согласно им, правильными вещественными числами считаются, например, выражения "10", "0.1", "+4", "-3.2", "8.26е-5" и т.п. Такие выражения, как, например, ".6" и "-.5", этим правилам не удовлетворяют, т.к. перед десятичной точкой должна стоять хотя бы одна цифра. В некоторых языках программирования такая запись допускается, но Delphi требует обязательного наличия целой части.

Теперь переведем эти правила на язык БНФ (листинг 4.1).

<Number> ::= [<Sign>] <Digit> {<Digit>}

 [<Separator> <Digit> {<Digit>}]

 [<Exponent> [<Sign>] <Digit> {<Digit>}]

<Digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

<Sign> ::= '+' | '-'

<Separator> ::= '.'

<Exponent> ::= 'E' | 'e'

На основе этих правил можно написать функцию

IsNumber

True

False

// Проверка символа на соответствие <Digit>

function IsDigit(Ch: Char): Boolean;

begin

 Result := Ch in ['0'..'9'];

end;

// Проверка символа на соответствие <Sign>

function IsSign(Ch: Char): Boolean;

begin

 Result := (Ch = '+') or (Ch = '-');

end;

// Проверка символа на соответствие <Separator>

function IsSeparator(Ch: Char): Boolean;

begin

 Result := Ch='.';

end;

// Проверка символа на соответствие <Exponent>

function IsExponent(Ch: Char): Boolean;

begin

 Result := (Ch = 'E') or (Ch = 'e');

end;

function IsNumber(const S: string): Boolean;

var

 P: Integer; // Номер символа выражения, который сейчас проверяется

begin

 Result := False;

 // Проверка, что выражение содержит хотя бы один символ — пустая строка

 // не является числом

 if Length(S) = 0 then Exit;

 // Начинаем проверку с первого символа

 Р := 1;

 // Если первый символ — <Sign>, переходим к следующему

 if IsSign(S[Р]) then Inc(Р);

 // Проверяем, что в данной позиции стоит хотя бы одна цифра

 if (Р > Length(S)) or not IsDigit(S[Р]) then Exit;

 // Переходим к следующей позиции, пока не достигнем конца строки

 // или не встретим не цифру

 repeat

  Inc(Р);

 until (Р > Length(S)) or not IsDigit(S[Р]);

 // Если достигли конца строки, выражение корректно — число.

 // не имеющее дробной части и экспоненты

 if Р > Length(S) then

 begin

  Result := True;

  Exit;

 end;

 // Если следующей символ — <Separator>, проверяем, что после него

 // стоит хотя бы одна цифра

 if IsSeparator(S[P]) then

 begin

  Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then Exit;

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

  // Если достигли конца строки, выражение корректно — число

  // без экспоненты

  if Р > Length(S) then

  begin

   Result := True;

   Exit;

  end;

 end;

 // Если следующий символ — <Exponent>, проверяем, что после него

 // стоит все то, что требуется правилами

 if IsExponent(S[Р]) then

 begin

  Inc(P);

  if P > Length(S) then Exit;

  if IsSign(S[P]) then Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then Exit;

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

  if P > Length(S) then

  begin

   Result := True;

   Exit;

  end;

 end;

 // Если выполнение дошло до этого места, значит, в выражении остались

 // еще какие-то символы. Так как никакие дополнительные символы

 // синтаксисом не предусмотрены, такое выражение не считается

 // корректным числом.

end;

Для каждого нетерминального символа мы ввели отдельную функцию, разбор начинается с символа самого верхнего уровня —

<Number>

Пример использования функции

IsNumber

В заключение рассмотрим альтернативный способ записи грамматики вещественного числа — графический (такой способ называется синтаксическим графом, или рельсовой диаграммой). Это направленный граф, узлами которого являются терминальные (круги) и нетерминальные (прямоугольники) символы. Двигаться от одного узла к другому можно только по линиям в направлениях, указанных стрелками. В таком графе достаточно легко разобраться, а по возможностям описания синтаксиса он эквивалентен БНФ. На рис. 4.1 показана запись синтаксиса вещественного числа с помощью рельсовой диаграммы.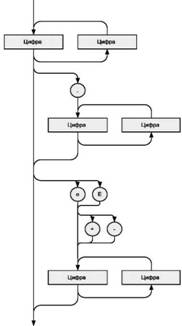

Рис. 4.1. Диаграмма синтаксиса вещественного числа

В качестве самостоятельного упражнения рекомендуем нарисовать с помощью рельсовой диаграммы грамматику символа "Цифра", используемого на рис. 4.1.

Теперь у нас уже достаточно знаний, чтобы создать простейший калькулятор, т. е. функцию, которая будет на входе принимать выражение, а на выходе, если это выражение корректно, возвращать результат его вычисления. Для начала ограничимся простым калькулятором, который умеет работать только с числовыми константами и знает только четыре действия арифметики. Изменение порядка вычисления операторов с помощью скобок также оставим на потом.

Таким образом, наш калькулятор будет распознавать и вычислять цепочки чисел, между которыми стоят знаки операции, которые над этими числами выполняются. В вырожденном случае выражение может состоять из одного числа и, соответственно, не содержать ни одного знака операции. Опишем эти правила с помощью БНФ и ранее определенного символа

<Number>

<Expr> ::= <Number> {<Operation> <Number>}

<Operation> ::= '+' | '-' | '*' | '/'

Примечание

В нашей грамматике не предусмотрено, что между оператором и его операндами может находиться пробел, т.е. выражение "2 + 2", в отличие от "2+2", не удовлетворяет данной грамматике. В отсутствие лексического анализатора игнорирование пробелов и прочих разделителей (переводов строки, комментариев) является трудоемкой рутинной операцией, поэтому во всех примерах без лексического анализатора мы будем требовать, чтобы выражения не содержали пробелов.

Для написания калькулятора нам понадобятся две новых функции —

IsOperator

Expr

IsNumber

Number

Number

Expr

Number

Number

ESyntaxError

Сама по себе задача преобразования строки в вещественное число достаточно сложна, и чтобы не отвлекаться на ее решение, мы воспользуемся функцией

StrToFloat

SysUtils

Number

StrToFloat

StrToFloat

IsSeparator

DecimalSeparator

StrToFloat

Extended

EConvertError

Extended

Новые функции приведены в листинге 4.3.

// Выделение из строки подстроки, соответствующей

// определению <Number>, и вычисление этого числа

// S — строка, из которой выделяется подстрока

// Р — номер позиции в строке, с которой должно

// начинаться число. После завершения работы функции

// этот параметр содержит номер первого после числа

function Number(const S: string; var P: Integer): Extended;

var

 InitPos: Integer;

begin

 // InitPos нам понадобится для выделения подстроки,

 // которая будет передана в StrToFloat

 InitPos := Р;

 if (Р <= Length(S)) and IsSign(S[P]) then Inc(P);

 if (P > Length(S)) or not IsDigit(S[P]) then

  raise ESyntaxError.Create(

   'Ожидается цифра в позиции ' + IntToStr(Р));

 repeat

  Inc(P);

 until (P > Length(S)) or not IsDigit(S[P]);

 if (P <= Length(S)) and IsSeparator(S[P]) then begin

  Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then

   raise ESyntaxError.Create(

    'Ожидается цифра в позиции ' + IntToStr(Р));

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

 end;

 if (P <= Length(S)) and IsExponent(S[P]) then

 begin

  Inc(P);

  if Р > Length(S) then

   raise ESyntaxError.Create('Неожиданный конец строки');

  if IsSign(S[P]) then Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then

   raise ESyntaxError.Create(

    'Ожидается цифра в позиции ' + IntToStr(Р));

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

 end;

 Result := StrToFloat(Copy(S, InitPos, P - InitPos));

end;

// Проверка символа на соответствие <Operator>

function IsOperator(Ch: Char): Boolean;

begin

 Result := Ch in ['+', '-', '*', '/'];

end;

// Проверка строки на соответствие <Expr>

// и вычисление выражения

function Expr(const S: string): Extended;

var

 P: Integer;

 OpSymb: Char;

begin

 P := 1;

 Result := Number(S, P);

 while (P <= Length(S)) and IsOperator(S[P]) do

 begin

  OpSymb := S[P];

  Inc(P);

  case OpSymb of

  '+': Result := Result + Number(S, P);

  '-': Result := Result - Number(S, P);

  '*': Result := Result * Number(S, P);

  '/': Result := Result / Number(S, P);

  end;

 end;

 if P <= Length(S) then

  raise ESyntaxError.Create(

   'Heкорректный символ в позиции ' + IntToStr(Р));

end;

Код приведен практически без комментариев, т.к. он очень простой, и все моменты, заслуживающие упоминания, мы уже разобрали в тексте. На прилагаемом компакт-диске находится программа SimpleCalcSample, которая демонстрирует работу нашего калькулятора. Калькулятор выполняет действия над числами слева направо, без учета приоритета операций, т.е. вычисление выражения "2+2*2" даст 8.

Грамматика выражения является простой для разбора, т.к. разбор выражения идет слева направо, и для соотнесения очередной части строки с тем или иным нетерминальным символом на любом этапе анализа достаточно знать только следующий символ. Такие грамматики называются LR(1)-грамматиками (в более общем случае требуется не один символ, а одна лексема). Класс этих грамматик был исследован Кнутом.

Грамматика Паскаля не относится к классу LR(1)-грамматик из-за уже упоминавшейся проблемы отнесения

else

if

if

else

else

if

else

if

for

while

with

else

Другое достоинство нашей простой грамматики — ее однозначность. Любая синтаксически верная строка не допускает неоднозначной трактовки. Неоднозначность могла бы возникнуть, например), если бы какая-то операция обозначалась символом "." (точка). Тогда было бы непонятно, должно ли выражение "1.5" трактоваться как число "одна целая пять десятых" или как выполнение операции над числами 1 и 5. Этот пример выглядит несколько надуманным, но неоднозначные грамматики, тем не менее, иногда встречаются на практике. Например, если запятая служит для отделения дробной части числа от целой и для разделения значений в списке параметров функций, то выражение

f(1,5)

f

"++",

а+++b

(а++)+b

а+(++b)

а+(+(+b))

Следующим нашим шагом станет модификация калькулятора таким образом, чтобы он учитывал приоритет операций, т. е. чтобы умножение и деление выполнялись раньше сложения и умножения.

Дня примера рассмотрим выражение "2*4+3*8/6". Наш синтаксис должен как-то отразить то, что аргументами операции сложения в данном случае являются не числа 4 и 3, а "2*4" и "3*8/6". В общем случае это означает, что выражение — это последовательность из одного или нескольких слагаемых, между которыми стоят знаки "+" или "-". А слагаемые — это, в свою очередь, последовательности из одного или нескольких чисел, разделенных знаками "*" и "/". А теперь запишем то же самое на языке БНФ (листинг 4.4).

<Expr> ::= <Term> {<Operator1> <Term>}

<Term> ::= <Number> {<Operator2> <Number>}

<Operator1> ::= '+' | '-'

<Operator2> ::= '*' | '/'

Определение символа

<Operator1>

<Sign>

<Sign>

<Expr>

<Operator1>

<Number>

<Sign>

Чтобы приспособить калькулятор к новым правилам, нужно заменить функцию

Operator

Operator1

Operator2

Term

Expr

Number

// Проверка символа на соответствие <Operator1>

function IsOperator1(Ch: Char): Boolean;

begin

 Result := Ch in ['+', '-'];

end;

// Проверка символа на соответствие <Operator2>

function IsOperator2(Ch: Char): Boolean;

begin

 Result := Ch in ['*', '/'];

end;

// Выделение подстроки, соответствующей <Term>,

// и ее вычисление

function Term(const S: string; var P: Integer): Extended;

var

 OpSymb: Char;

begin

 Result := Number(S,P);

 while (P <= Length(S)) and IsOperator2(S[P]) do

 begin

  OpSymb := S[P];

  Inc(P);

  case OpSymb of

  '*': Result := Result * Number(S, P);

  '/': Result := Result / Number(S, P);

 end;

end;

// Проверка строки на соответствие <Expr>

// и вычисление выражения

function Expr(const S: string): Extended;

var

 P: Integer;

 OpSymb: Char;

begin

 P := 1;

 Result := Term(S, P);

 while (P <= Length(S)) and IsOperator1(S[P]) do

 begin

  OpSymb := S[P];

  Inc(P);

  case OpSymb of

  '+': Result := Result + Term(S, P);

  '-': Result := Result - Term(S, P);

  end;

 end;

 if P <= Length(S) then

  raise ESyntaxError.Create(

   'Некорректный символ в позиции ' + IntToStr(Р));

end;

Если вы разобрались с предыдущими примерами, приведенный здесь код будет вам понятен. Некоторых комментариев требует только функция

Term

<Term>

Expr

Term

Number

P

Пример калькулятора, учитывающего приоритет операций, находится на компакт-диске под именем PrecedenceCalcSample. Поэкспериментировав с ним, легко убедиться, что теперь вычисление "2+2*2" дает правильное значение 6.

В заключение заметим, что язык, определяемый такой грамматикой, полностью совпадает с языком, определяемым грамматикой из предыдущего примера, т.е. любое выражение, принадлежащее первому языку, принадлежит и второму, и наоборот. Усложнение синтаксиса, которое мы здесь ввели, требуется именно для отражения семантики выражений, а не для расширения самого языка.

Порядок выполнения операций в выражении может меняться с помощью скобок. Внутри них должно находиться выражение, которое, будучи выделенным в отдельную строку, само по себе отвечает требованиям синтаксиса к выражению в целом.

Выражение, заключенное в скобки, допустимо везде, где допускается появление отдельного числа (из этого, в частности, следует, что допускаются вложенные скобки). Таким образом, мы должны расширить нашу грамматику так, чтобы аргументом операций сложения и умножения могли служить не только числа, но и выражения, заключенные в скобки. Это автоматически позволит использовать такие выражения и в качестве слагаемых, потому что слагаемое — это последовательность из одного или нескольких множителей, разделенных знаками умножения и деления. На языке БНФ все сказанное иллюстрирует листинг 4.6.

<Expr> ::= <Term> {<Operation1> <Term>}

<Term> ::= <Factor> {<Operation2> <Factor>}

<Factor> ::= <Number> | ' (' <Expr> ')'

В этих определениях появилась рекурсия, т.к. в определении

<Expr>

<Term>

<Factor>

<Term>

Наша грамматика не учитывает, что перед скобками может стоять знак унарной операции "

+

-

3*-(2+4)

<Factor>

<Factor> ::= <Number> | [Sign] '(' <Expr> ')'

Однако такой подход страдает отсутствием общности. В дальнейшем мы усложним наш синтаксис, введя другие типы множителей (функции, переменные). Перед каждым из них, в принципе, может стоять знак унарной операции, поэтому логичнее определить синтаксис таким образом, чтобы унарная операция допускалась вообще перед любым множителем. В этом случае можно будет слегка упростить определение

<Number>

+

-

С учетом этого новая грамматика запишется следующим образом (листинг 4.7).

<Expr> ::= <Term> {<Operation1> <Term>}

<Term> ::= <Factor> {<Operation2> <Factor>}

<Factor> ::= <UnaryOp> <Factor> | <Number> | '(' <Expr> ')'

<Number> ::= <Digit> {<Digit>} [<Separator> <Digit> {<Digit>}]

 [<Exponent> [<Sign>] <Digit> {<Digit>}]

<UnaryOp> ::= '+' | '-'

Здесь опущены определения некоторых вспомогательных символов, которые не изменились.

Мы видим, что грамматика стала "более рекурсивной", т.е. в определении символа

<Factor>

Factor

Символ

<UnaryOp>

<Operator1>

<Sign>

not

Побочным эффектом нашей грамматики стало то, что, например,

-5

--5

-(-5)

--5

2+-+-2

2+(-(+(-2)))

// Так как грамматика рекурсивна, функция Expr

// должна быть объявлена заранее

function Expr(const S: string; var Р: Integer): Extended; forward;

// Выделение подстроки, соответствующей <Factor>,

// и ее вычисление

function Factor(const S: string; var P: Integer): Extended;

begin

 if P > Length(S) then

  raise ESyntaxError.Create('Неожиданный конец строки');

 // По первому символу подстроки определяем,

 // какой это множитель

 case S[Р] of

 '+': // унарный "+"

 begin

  Inc(Р);

  Result := Factor(S, P);

 end;

 '-': // унарный "-"

 begin

  Inc(P);

  Result := -Factor(S, P);

 end;

 '(': // выражение в скобках

 begin

  Inc(P);

  Result := Expr(S, P);

  // Проверяем, что скобка закрыта

  if (Р > Length(S)) or (S[P] <> ')') then

   raise ESyntaxError.Create(

    'Ожидается ")" в позиции ' + IntToStr(P));

  Inc(P);

 end;

 '0'..'9': // Числовая константа

  Result := Number(S, P);

 else

  raise ESyntaxError.Create(

   'Некорректный символ в позиции ' + IntToStr(Р));

 end;

end;

// Выделение подстроки, соответствующей <Term>,

// и ее вычисление

function Term(const S: string; var P: Integer): Extended;

var

 OpSymb: Char;

begin

 Result := Factor(S, P);

 while (P <= Length(S)) and IsOperator2(S[P]) do

 begin

  OpSymb := S[P];

  Inc(P);

  case OpSymb of

  '*': Result := Result * Factor(S, P);

  '/': Result := Result / Factor(S, P);

  end;

 end;

end;

// Выделение подстроки, соответствующей <Expr>,

// и ее вычисление

function Expr(const S: string; var Р: Integer): Extended;

var

 OpSymb: Char;

begin

 Result := Term(S, P);

 while (P <= Length(S)) and IsOperator1(S[P]) do

 begin

OpSymb := S[P];

  Inc(P);

  case OpSymb of

  '+': Result := Result + Term(S, P);

  '-': Result := Result - Term(S, P);

  end;

 end;

end;

// Вычисление выражения

function Calculate(const S: string): Extended;

var

 P: Integer;

begin

 P := 1;

 Result := Expr(S, P);

 if P <= Length(S) then

  raise ESyntaxError.Create(

   'Некорректный символ в позиции ' + IntToStr(Р));

end;

По сравнению с предыдущим примером функция

Term

Number

Factor

Factor

Factor

Функция

Expr

P

Функция

Expr

Calculate

P

Пример калькулятора со скобками записан на компакт-диске под названием BracketsCalcSample. Анализируя его код, можно заметить, что по сравнению с предыдущим примером незначительно изменена функция

Number

Последняя версия нашего калькулятора может считать сложные выражения, но чтобы он имел практическую ценность, этого мало. В этом разделе мы научим наш калькулятор использовать функции и переменные. Также будет введена операция возведения в степень, обозначающаяся значком "

^

Имена переменных и функций — это идентификаторы. Идентификатор определяется по общепринятым правилам: он должен начинаться с буквы латинского алфавита или символа "

_

_

<Letter> ::= 'А' | ... | ' Z' | 'а' ... | ' z' | '_'

<Identifier> ::= <Letter> {<Letter> | <Digit>}

Примечание

Следствием этой грамматики является то, что отдельно взятый символ "

_

" считается корректным идентификатором. И хотя это может на первый взгляд показаться абсурдным, тем не менее, именно таковы общепринятые правила. Легко убедиться, что, например, Delphi допускает объявление переменных с именами "

_

", "

__

" и т.п.

В нашей грамматике переменной будет называться отдельно стоящий идентификатор, функцией — идентификатор, после которого в скобках записан аргумент, в качестве которого может выступать любое допустимое выражение (для простоты мы будем рассматривать только функции с одним аргументом, т.к. обобщение грамматики на большее число аргументов очевидно). Другими словами, определение будет выглядеть так:

<Variable> ::= <Identifier>

<Function> ::= <Identifier> ' (' <Expr> ')'

Из приведенных определений видно, что грамматика, основанная на них, не относится к классу LR(1)-грамматик, т.к. обнаружив в выражении идентификатор, анализатор не может сразу решить, является ли этот идентификатор переменной или именем функции, это выяснится только при проверке следующего символа — скобка это или нет. Тем не менее реализация такой грамматики достаточно проста, и это не будет доставлять нам существенных неудобств.

Переменные и функции, так же, как и выражения, заключенные в скобки, выступают в роли множителей. Соответственно, их появление в грамматике учитывается расширением смысла символа

<Factor>

<Factor> ::= <UnaryOp> <Factor> |

 <Variable> |

 <Function> |

 <Number> |

 '(' <Expr> ')'

Теперь рассмотрим свойства оператора возведения в степень. Во-первых, его приоритет выше, чем у операций сложения и деления, т.е. выражение

a*b^c

a*(b^c)

a^b*c

(a^b)*c

a^b^c

a^(b^c)

(a^b)^c

-a^b

-(a^b)

(-а)^b

a^-b

a^(-b)

Таким образом, мы видим, что показателем степени может быть любой отдельно взятый множитель, а основанием — число, переменная, функция или выражение в скобках, т.е. любой множитель, за исключением начинающегося с унарного оператора. Запишем это в виде БНФ.

<Factor> ::= <UnaryOp> <Factor> | <Base> ['^' <Factor>]

<Base> ::= <Variable> | <Function> | <Number> | '(' <Expr> ')'

Правая ассоциативность также заложена в этих определениях. Рассмотрим, как будет разбираться выражение

a^b^c

Factor

Base

b^c

b^c

Так как определения символов

<Expr>

<Term>

Factor

Base

Identifier

Func

function

Для простоты обойдемся тремя функциями:

sin

cos

ln

Если у нас появились переменные, то мы должны как-то хранить их значения, чтобы при вычислении выражения использовать их. В нашем примере мы будем хранить их в объекте типа

TStrings

Values

// вычисление функции, имя которой передается через FuncName

function Func(const FuncName, S: string; var Integer): Extended;

var

 Arg: Extended;

begin

 // Вычисляем аргумент

 Arg := Expr(S, P);

 // Сравниваем имя функции с одним из допустимых

 if AnsiCompareText(FuncName, 'sin') = 0 then

  Result := Sin(Arg)

 else if AnsiCompareText(FuncName, 'соs') = 0 then

  Result := Cos(Arg)

 else if AnsiCompareText(FuncName, 'ln') = 0 then

  Result := Ln(Arg)

 else

  raise ESyntaxError.Create('Неизвестная функция ' + FuncName);

end;

// Выделение из строки идентификатора и определение,

// является ли он переменной или функцией

function Identifier(const S: string: var P: Integer): Extended;

var

 InitP: Integer;

 IDStr, VarValue: string;

begin

 // Запоминаем начало идентификатора

 InitP := P;

 // Первый символ был проверен ещё в функции Base.

 // Сразу переходим к следующему

 Inc(P);

 while (P <= Length(S)) and

  (S[P] in ('A'..'Z', 'a'..'z', '_', '0'..'9']) do

  Inc(P);

 // Выделяем идентификатор из строки

 IDStr := Copy(S, InitP, P - InitP);

 // Если за ним стоит открываемая скобка — это функция

 if (Р <= Length(S)) and (S[P) - '(' then

 begin

  Inc(P);

  Result := Func(IDStr, S, P);

  // Проверяем, что скобка закрыта

  if (Р > Length(S)) or (S[P] <> ')') then

   raise ESyntaxError.Create(

    'Ожидается ")" в позиции ' + IntToStr(P));

  Inc(P);

 end

 // если скобки нет - переменная

 else

 begin

  VarValue := Form1.ListBoxVars.Items.Values[IDStr];

  if VarValue = '' then

   raise ESyntaxError.Create(

    'Необъявленная переменная ' + IDStr +

    ' в позиции ' + IntToStr(P))

  elsе Result := StrToFloat(VarValue);

 end;

end;

// Выделение подстроки, соответствующей <Base>,

// и ее вычисление

function Base(const S: string; var P: Integer): Extended;

begin

 if P > Length(S) then

  raise ESyntaxError.Create('Неожиданный конец строки');

 // По первому символу подстроки определяем,

 // какое это основание

 case S[P] of

 '(': // выражение в скобках

 begin

  Inc(Р);

  Result := Expr(S, Р);

  // Проверяем, что скобка закрыта

  if (Р > Length(S)) or (S[P) <> ')') then

   raise ESyntaxError.Create(

    'Ожидается ")" в позиции ' + IntToStr(Р));

  Inc(Р);

 end;

'0'..'9': // Числовая константа

  Result := Number(S, P);

 'A'..'Z', 'a'..'z', '_': // Идентификатор (переменная или функция)

  Result := Identifier(S, P);

 else

  raise ESyntaxError.Create(

   'Некорректный символ в позиции ' + IntToStr(Р));

 end;

end;

// Выделение подстроки, соответствующей <Factor>,

// и ее вычисление

function Factor(const S: string; var P: Integer): Extended;

begin

 if P > Length(S) then

  raise ESyntaxError.Create('Неожиданный конец строки');

 // По первому символу подстроки определяем,

 // какой это множитель

 case S[P] of

 '+'; // унарный "+"

 begin

  Inc(Р);

  Result := Factor(S, P);

 end;

 '-': // унарный "-"

 begin

  Inc(P);

  Result := -Factor(S, P);

 end;

 else

 begin

  Result := Base(S, P); 

  if (P <= Length(S)) and (S[P] = '^') then

  begin

   Inc(P);

   Result := Power(Result, Factor(S, P));

  end;

 end;

 end;

end;

Пример калькулятора называется FullCalcSample. Его интерфейс (рис. 4.2) содержит новые элементы, с помощью которых пользователь может задавать значения переменных. В левой нижней части окна находится список переменных с их значениями (при запуске программы этот список пустой). Правее расположены поля ввода Имя переменной и Значение переменной, а также кнопка Установить. В первое поле следует ввести имя переменной, во второе — ее значение. При нажатии на кнопку Установить переменная будет внесена в список, а если переменная с таким именем уже есть в списке, то ее значение будет обновлено. Все переменные, которые есть в списке, могут использоваться в выражении. Если требуемая переменная в списке не найдена, попытка вычислить выражение приводит к ошибке.

Рис. 4.2. Главное окно программы FullCalcSample

Заметим, что символ

<Factor>

<Factor> ::= [<UnaryOp>] <Base> ['^' <Factor>]

В нашем случае, когда есть только два унарных оператора и применение срезу двух (разных или одинаковых) практически бессмысленно, такой синтаксис реализовать было бы проще (пример реализации такого синтаксиса дан в программе FullCalcSample в виде комментария). При этом исчезла бы возможность ставить несколько знаков унарных операций подряд. В общем случае такой подход неверен, т.к. при большем количестве унарных операций это может пригодиться, да и выглядит естественно. Поэтому в качестве основного был выбран несколько более сложный, но и более функциональный вариант.

Прежде чем двигаться дальше, рассмотрим недостатки последней версии нашего калькулятора. Во-первых, бросается в глаза некоторое дублирование функций. Действительно, с одной стороны, выделением числа из подстроки занимается функция

Number

Base

Identifier

Base

Второй недостаток — нельзя вставлять разделители, облегчающие чтение выражения. Например, строка "2 + 2" не является допустимым выражением — следует писать "2+2" (без пробелов). Если же попытаться учесть возможность вставки пробелов, придется в разные функции добавлять много однотипного рутинного кода, который существенно усложнит восприятие программы.

Третий недостаток — сложность введения новых операторов, которые обозначаются не одним символом, а несколькими, например,

>=

and

div

Expr

Term

Решить все эти проблемы позволяет лексический анализатор, который выделяет из строки все лексемы, пропуская пробелы и иные разделители, и определяет тип каждой лексемы, не заботясь о том, насколько уместно ее появление в данной позиции выражения. А после лексического анализа начинает работать анализатор синтаксический, который будет иметь дело не с отдельными символами строки, а с целыми лексемами

В качестве примера рассмотрим реализацию следующей грамматики (листинг 4.10).

<Expr> ::= <MathExpr> [<Comparison> <MathExpr>]

<Comparison> ::= '=' | '>' | '<' | '>=' | '<=' | '<>'

<MathExpr> ::= <Term> {<Operator1> <Term>}

<Operator1> ::= '+' | '-' | 'or' | 'xor'

<Term> ::= <Factor> {<Operator2> <Factor>}

<Operator2> ::= '*' | '/' | 'div' | 'mod' | 'and'

<Factor> ::= <UnaryOp> <Factor> | <Base> ['^' <Factor>]

<UnaryOp> ::= '+' | '-' | 'not'

<Base> ::= <Variable> | <Function> | <Number> | '(' <MathExpr> ')'

<Function> ::= <FuncName> '(' <MathExpr> ')'

<FuncName> ::= 'sin' | 'cos' | 'ln'

<Variable> ::= <Letter> {<Letter> | <Digit>}

<Letter> ::= 'A' | ... | 'Z' | 'a' | ... | 'z' | '_'

<Digit> ::= '0' | ... | '9'

<Number> ::= <Digit> {<Digit>} [<DecimalSeparator> <Digit> {<Digit>}]

 (('E' | 'e') ['+' | '-'] <Digit> {<Digit>)]

Примечание

Здесь используется нетерминальный символ

<DecimalSeparator>

, который мы не определили. Он полагается равным точке или запятой в зависимости от системных настроек.

Эта грамматика на первый взгляд может показаться существенно более сложной, чем все, что мы реализовывали ранее, но это не так: просто здесь приведены определения всех (за исключением

<DecimalSeparator>

<Number>

<Expr>

<MathExpr>

<Expr>

<MathExpr>

<MathExpr>

<Expr>

<MathExpr>

<MathExpr>

True

False

В новой грамматике также расширен набор операторов. Операторы

or

xor

and

not

div

mod

Лексический анализатор должен выделять из строки следующие лексемы:

1. Все знаки операций, которые используются в определении символов

<Comparison>

<Operator1>

<Operator2>

<UnaryOp>

^

2. Открывающую и закрывающую скобки.

3. Имена функций.

4. Идентификаторы (т.е. переменные).

5. Числовые константы.

Напомним, что лексический анализатор не должен определять допустимость появления лексемы в данном месте строки. Он просто сканирует строку, выделяет из нее последовательности символов, распознаваемые как отдельные лексемы, и сохраняет информацию о них в специальном списке, которым потом пользуется синтаксический анализатор. Так, например, встретив цифру, лексический анализатор выделяет числовую константу. Встретив букву, он выделяет последовательность буквенно-цифровых символов. Затем сравнивает эту последовательность с одним из зарезервированных слов (

and

div

Из нашей грамматики следует, что имена функций являются зарезервированными словами, т.е. объявить переменные с именами

sin

cos

ln

Отдельные лексемы выделяются по следующему алгоритму: сначала, начиная с текущей позиции, пропускаются все разделители — пробелы и символы перевода строки. Затем по первому символу определяется лексема — знак, слово (которое потом может оказаться зарезервированным словом или идентификатором) или число. Дальше лексический анализатор выбирает из строки все символы до тех пор, пока они удовлетворяют правилам записи соответствующей лексемы. Следующая лексема ищется с позиции, идущей непосредственно за предыдущей лексемой.

В зависимости от типа лексем разделители между ними могут быть обязательными или необязательными. Например, в выражении "2+3" разделители между лексемами "2", "+" и "5" не нужны, потому что они могут быть отделены друг от друга и без этого. А в выражении

6 div 3

6div

Чтобы продемонстрировать возможности лексического анализатора, добавим поддержку комментариев. Комментарий — это последовательность символов, начинающаяся с "{" и заканчивающаяся "}", которая может содержать внутри себя любые символы, кроме "}". Комментарий считается разделителем, он допустим в любом месте, где возможно появление других разделителей, т.е. в начале и в конце строки и между лексемами.

Пример калькулятора с лексическим анализатором также находится на компакт-диске и называется LexicalSample.

Лексический анализатор на входе получает строку, на выходе он должен дать список структур, каждая из которых описывает одну лексему. В нашем примере эти структуры выглядят следующим образом (листинг 4.11).

TLexemeType = (

 ltEqual, ltLess, ltGreater, ltLessOrEqual,

 ltGreaterOrEqual, ltNotEqual, ltPlus, ltMinus,

 ltOr, ltXor, ltAsterisk, ltSlash, ltDiv, ltMod,

 ltAnd, ltNot, ltCap,

ltLeftBracket, ltRightBracket,

 ltSin, ltCos, ltLn,

 ltIdentifier, ltNumber, ltEnd);

TLexeme = record

 LexemeType: TLexemeType;

 Pos: Integer;

 Lexeme: string;

end;

LexemeType

TLexemeType

Pos

Поле

Lexeme

ltIdentifier

ltNumber

LexemeType

Лексический анализатор реализован в виде класса

TLexicalAnalyzer

Lexeme

Next

type

 TLexicalAnalyzer = class

 private

  FLexemeList: TList;

  // Номер текущей лексемы в списке

  FIndex: Integer;

  function GetLexeme: PLexeme;

  // Пропуск всего, что является разделителем лексем

  procedure SkipWhiteSpace(const S: string; var P: Integer);

  // Выделение лексемы, начинающейся с позиции P

  procedure ExtractLexeme(const S: string; var P: Integer);

  // Помещение лексемы в список

  procedure PutLexeme(LexemeType: TLexemeType; Pos: Integer; const Lexeme: string);

  // Выделение лексемы-числа

  procedure Number(const S: string; var P: Integer);

  // Выделение слова и отнесение его к идентификаторам

  // или зарезервированным словам

  procedure Word(const S: string; var P: Integer);

 public

  constructor Create(const Expr: string);

  destructor Destroy; override;

  // Переход к следующей лексеме

  procedure Next;

  // Указатель на текущую лексему

  property Lexeme: PLexeme read GetLexeme;

 end;

constructor TLexicalAnalyzer.Create(const Expr: string);

var

 P: Integer;

begin

 inherited Create;

 // Создаем список лексем

 FLexemeList := TList.Create;

 // И сразу же заполняем его

 Р := 1;

 while Р <= Length(Expr) do

 begin

  SkipWhiteSpace(Expr, P);

  ExtractLexeme(Expr, P);

 end;

 // Помещаем в конец списка специальную лексему

 PutLexeme(ltEnd, Р, '');

 FIndex := 0;

end;

destructor TLexicalAnalyzer.Destroy;

var

 I: Integer;

begin

 for I := 0 to FLexemeList.Count - 1 do

  Dispose(PLexeme(FLexemeList[I]));

 FLexemeList.Free;

 inherited Destroy;

end;

// Получение указателя на текущую лексему

function TLexicalAnalyzer.GetLexeme: PLexeme;

begin

 Result := FLexemeList[FIndex];

end;

// Переход к следующей лексеме

procedure TLexicalAnalyzer.Next;

begin

 if FIndex < FLexemeList.Count - 1 then Inc(FIndex);

end;

// Помещение лексемы в список. Параметры метода задают

// одноименные поля типа TLexeme.

procedure TLexicalAnalyzer.PutLexeme(LexemeType: TLexemeType; Pos: Integer; const Lexeme: string);

var

 NewLexeme: PLexeme;

begin

 New(NewLexeme);

 NewLexeme^.LexemeType := LexemeType;

 NewLexeme^.Pos := Pos;

 NewLexeme^.Lexeme := Lexeme;

 FLexemeList.Add(NewLexeme);

end;

// пропускает пробелы, символы табуляции, комментарии и переводы строки,

// которые могут находиться в начале и в конце строки и между лексемами

procedure TLexicalAnalyzer.SkipWhiteSpace(const S: string; var P: Integer);

begin

 while (P <= Length(S)) and (S[P] in [' ', #9, #13, #10, '{']) do

  if S[P] = '{' then

  begin

   Inc(P);

   while (P <-=Length(S)) and (S[P) <> '}') do Inc(P);

   if P > Length(S) then

    raise ESyntaxError.Create('Незавершенный комментарий');

   Inc(P);

  end

  else Inc(P);

end;

// Функция выделяет одну лексему и помещает ее в список

procedure TLexicalAnalyzer.ExtractLexeme(const S: string; var P: Integer);

begin

 if P > Length(S) then Exit;

 case S[P] of

 '(': begin

  PutLexeme(ltLeftBracket, P, '');

  Inc(P);

 end;

 ')': begin

  PutLexeme(ltRightBracket, P, '');

  Inc(P);

 end;

 '*': begin

  PutLexeme(ltAsterisk, P, '');

  Inc(P);

 end;

 '+': begin

  PutLexeme(ltPlus, P, '');

  Inc(P);

 end;

 '-': begin

  PutLexeme(ltMinus, P, '');

  Inc(P);

 end;

 '/': begin

  PutLexeme(ltSlash, P, '');

  Inc(P);

 end;

 '0'..'9': Number(S, P);

 '<':if (P < Length(S)) and (S[P + 1] = '=') then

 begin

  PutLexeme(ltLessOrEqual, P, '');

  Inc(P, 2);

 end

 else

  if (P < Length(S)) and (S[P + 1] = '>') then

  begin

   PutLexeme(ltNotEqual, P, '');

   Inc(P, 2);

  end

  else

  begin

   PutLexeme(ltLess, P, '');

   Inc(P);

  end;

 '=': begin

  PutLexeme(ltEqual, P, '');

  Inc(P);

 end;

 '>': if (P < Length(S)) and (S[P + 1] = '=') then

 begin

  PutLexeme(ltGreaterOrEqual, P, '');

  Inc(P, 2);

 end

 else

 begin

  PutLexeme(ltGreater, P, '');

  Inc(P);

 end;

 'A'..'Z, 'a'..'z', '_': Word(S, P);

 '^': begin

  PutLexeme(ltCap, P, '');

  Inc(P);

 end;

 else

  raise ESyntaxError.Create('Некорректный символ в позиции ' +

   IntToStr(Р));

 end;

end;

// Выделение лексемы-числа

procedure TLexicalAnalyzer.Number(const S: string; var P: Integer);

var

 InitPos, RollbackPos: Integer;

 function IsDigit(Ch: Char): Boolean;

 begin

  Result := Ch in ['0'..'9'];

 end;

begin

 InitPos := P;

 // Выделяем целую часть числа

 repeat

  Inc(P);

 until (P < Length(S)) or not IsDigit(S[P]);

 // Проверяем наличие дробной части и выделяем её

 if (Р <= Length(S)) and (S[P] = DecimalSeparator) then

 begin

  Inc(P);

  if (Р > Length(S)) or not IsDigit(S[P]) then Dec(P)

  else repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S(P));

 end;

 // Выделяем экспоненту

 if (P <= Length(S)) and (UpCase(S[P]) = 'E') then

 begin

  // Если мы дошли до этого места, значит, от начала строки

  // и до сих пор набор символов представляет собой

  // синтаксически правильное число без экспоненты.

  // Прежде чем начать выделение экспоненты, запоминаем

  // текущую позицию, чтобы иметь возможность вернуться к ней

  // если экспоненту выделить не удастся.

  RollBackPos := P;

  Inc(Р);

  if Р > Length(S) then P := RollBackPos

  else

  begin

   if S[P] in ['+', '-'] then Inc(P);

   if (P > Length(S)) or not IsDigit(S(P)) then P := RollbackPos

   else repeat

    Inc(P);

   until (P > Length(S)) or not IsDigit(S[P]);

  end;

 end;

 PutLexeme(ltNumber, InitPos, Copy(S, InitPos, P- InitPos));

end;

// Выделение слова из строки и проверка его на совпадение

// с зарезервированными словами языка

procedure TLexicalAnalyzer.Word(const S: string; var P: Integer);

var

 InitPos: Integer;

 ID: string;

begin

 InitPos := P;

 Inc(P);

 while (P <= Length(S)) and

(S[P] in ['0'..'9', 'A'..'Z', 'a'..'z', '_']) do

  Inc(P);

 ID := Copy(S, InitPos, P - InitPos);

 if AnsiCompareText(ID, 'or') = 0 then

  PutLexeme(ltOr, InitPos, '')

 else if AnsiCompareText(ID, 'xor') = 0 than

  PutLexeme(ltXor, InitPos, '')

 else if AnsiCompareText(ID, 'div') = 0 then

  PutLexeme(ltDiv, InitPos, '')

 else if AnsiCompareText(ID, 'mod') = 0 then

  PutLexeme(ltMod, InitPos, '')

 else if AnsiCompareText(ID, 'and') = 0 then

  PutLexeme(ltAnd, InitPos, '')

 else if AnsiCompareText(ID, 'not') = 0 then

  PutLexeme(ltNot, InitPos, '')

 else if AnsiCompareText(ID, 'sin') = 0 then

  PutLexeme(ltSin, InitPos, '')

 else if AnsiCompareText(ID, 'cos') = 0 then

  PutLexeme(ltCos, InitPos, '')

 else if AnsiCompareText(ID, 'ln') = 0 then

  PutLexeme(ltLn, InitPos, '')

 else PutLexeme(ltIdentifier, InitPos, ID);

end;

В конец списка лексем помещается специальная лексема типа

ltEnd

P

S

ltEnd

ltEnd

Expr

Примечание

Аналогичный алгоритм возможен и в предыдущих версиях калькулятора: достаточно добавить в конец строки символ, который в ней заведомо не должен был появляться (например,

#1

), и проверять в функции

Expr

или

Calculate

, что разбор выражения остановился именно на этом символе.

Лексический анализ выражения заключается в чередовании вызовов функций

SkipWhiteSpace

ExtractLexeme

Обратите внимание, как в лексическом анализаторе реализован метод

Number

Number

Отметим, что для нашей грамматики непринципиально, зафиксирует ли в таком выражении ошибку лексический или синтаксический анализатор. Но в общем случае может существовать грамматика, в которой такое выражение допустимо, поэтому лексический анализатор должен действовать именно так, т.е. выполнять откат, если попытка выделить число зашла на каком-то этапе в тупик (самый простой пример — наличие в языке бинарного оператора, начинающегося с символа "е" — тогда пользователь сможет написать этот оператор после числа без пробела, и чтобы справиться с такой ситуацией, понадобится откат). Функция

Number

ExtractLexeme

ltNumber

Number

Term

const

 Operator2 = (ltAsterisk, ltSlash, ltDiv, ltMod, ltAnd);

function Term(LexicalAnalyzer: TLexicalAnalyzer): Extended;

var

 Operator: TLexemeType;

begin

 Result := Factor(LexicalAnalyzer);

 while LexicalAnalyzer.Lexeme.LexemeType in Operator2 do

 begin

  Operator := LexicalAnalyzer.Lexeme.LexemeType;

  LexicalAnalyzer.Next;

  case Operator of

  ltAsterisk: Result := Result * Factor(LexicalAnalyzer);

  ltSlash: Result := Result / Factor(LexicalAnalyzer);

  ltDiv: Result := Trunc(Result) div Trunc(Factor(LexicalAnalyzer));

  ltMod: Result := Trunc(Result) mod Trunc(Factor(LexicalAnalyzer));

  ltAnd: Result := Trunc(Result) and Trunc(Factor(LexicalAnalyzer));

  end;

 end;

end;

Если сравнить этот вариант

Term

Использование лексического анализатора может повысить скорость многократного вычисления одного выражения при разных значениях входящих в него переменных (например, при построении графика функции, ввезенной пользователем). Действительно, лексический анализ в этом случае достаточно выполнить один раз, а потом пользоваться готовым списком. Можно сделать такие операции еще более эффективными, переложив вычисление числовых констант на лексический анализатор. Для этого в структуру

TLexeme

Number

Extended

Number

StrToFloat

Base

TLexicalAnalyzer.Number

В предыдущем примере выражение сначала от начала до конца просматривается лексическим анализатором и переводится в иную форму (список лексем). Затем этот список обрабатывается синтаксическим анализатором. Таким образом, калькулятор получается двухпроходным, хотя из синтаксиса и семантики выражения необходимость нескольких проходов не вытекает. Попробуем переделать его так, чтобы он стал однопроходным.

Примечание

В некоторых языках многопроходность — обязательное требование к реализации компилятора. Например, в языке C++ реализацию функций класса можно вставлять в само описание класса. При этом внутри этих функций можно обращаться к тем полям и функциям класса, которые объявлены ниже. Таким образом, откомпилировать подобный код может только компилятор как минимум с двумя проходами, чтобы на первом проходе можно было найти все поля класса, а на втором — откомпилировать функции класса.

В предыдущей реализации калькулятора синтаксический анализатор работал с лексическим через процедуру

Next

Lexeme

Next

Lexeme

Next

В реализации лексического анализатора требуются следующие изменения. Во-первых, теперь конструктор не запускает полный цикл лексического анализа, а только сохраняет переданную строку и выделяет из нее первую лексему. Во-вторых, выражение и позиция в выражении теперь должны сохраняться между вызовами методов лексического анализатора и поэтому становятся полями этого класса. В-третьих, метод

Next

Lexeme

Пример однопроходного калькулятора с лексическим анализатором находится на компакт-диске в папке

SinglePassSample

TLexicalAnalyzer

type

 TLexicalAnalyzer = class

 private

  // Выражение для вычисления

  FExpr: string;

  // Текущая позиция

  FP: Integer;

  // Текущая лексема

  FCurrLexeme: TLexeme;

  function GetLexeme: PLexeme;

  procedure SkipWhiteSpace;

  procedure ExtractLexeme;

  procedure PutLexeme(LexemeType: TLexemeType; Pos: Integer; const Lexeme: string);

  procedure Number;

  procedure Word;

 public

  constructor Create(const Expr: string);

  procedure Next;

  property Lexeme: PLexeme read GetLexeme;

 end;

constructor TLexicalAnalyzer.Create(const Expr: string);

begin

 inherited Create;

 FP := 1;

 FExpr := Expr;

 Next;

end;

// Получение указателя на текущую лексему

function TLexicalAnalyzer.GetLexeme: PLexeme;

begin

 Result := @FCurrLexeme;

end;

// Получение следующей лексемы

procedure TLexicalAnalyzer.Next;

begin

 if FP <= Length(FExpr) then

 begin

  SkipWhiteSpace;

  ExtractLexeme;

 end

 else PutLexeme(ltEnd, FP, '');

end;

// Замещение текущей лексемы новой лексемой

procedure TLexicalAnalyzer.PutLexeme(LexemeType: TLexemeType; Pos: Integer; const Lexeme: string);

begin

 FCurrLexeme.LexemeType := LexemeType;

 FCurrLexeme.Pos := Pos;

 FCurrLexeme.Lexeme := Lexeme;

end;

Теперь класс

TLexicalAnalyzer

PutLexeme

Next

SkipWhiteSpace

ExtractLexeme

Синтаксический анализатор при этом остается без изменений, т.к. интерфейс лексического анализатора не изменился.

Чтобы не реализовывать дважды одну и ту же грамматику, введем в наш синтаксис еще одну возможность — поддержку функций с несколькими аргументами. Конкретно — функцию с двумя аргументами

Log(а, x)

x

a

<Function> ::= <FuncName> '(' <MathExpr> {<ListSeparator> <MathExpr>} ')'

<FuncName> ::= 'sin' | 'cos' | 'ln' | 'log' | 'mean'

Отдельного комментария требует символ

<ListSeparator>

f(1,5)

f

Особенность нашего нового синтаксиса в том, что он допускает любое число аргументов для любой функции, т.е., например, выражение

sin(0, 1, 2, 4)

Для реализации новых синтаксических и семантических правил в код вносятся следующие изменения. Во-первых, появляются новые лексемы

ltLog

ltMean

ltListSeparator

Func

Для лучшего понимания работы лексического и синтаксического анализатора рекомендуем самостоятельно выполнить следующие задания (или хотя бы просто подумать, как их выполнить).

1. Расширить определение

<Expr>

or

and

xor

2. Изменить грамматику таким образом, чтобы имя функции стало идентификатором, а не зарезервированным словом.

3. Сделать комментарии вложенными. Сейчас в последовательности символов "{a{b}c}" считается, что комментарий заканчивается перед символом "с", т.к. лексический анализатор игнорирует все открывающие фигурные скобки в комментариях. Сделать так, чтобы комментарий считался закрытым только тогда, когда число закрывающих скобок сравняется с числом открывающих.

4. Добавить поддержку шестнадцатеричных целых констант. Для их записи использовать, как и в Delphi, символ "$", после которого должна идти последовательность из одной или нескольких шестнадцатеричных цифр.

5. Добавить возможность изменения приоритета операций с помощью не только круглых, но и квадратных скобок. Рассмотреть два варианта: когда круглые и квадратные скобки полностью взаимозаменяемы (т.е., например, допустимо выражение

2*(2+2]

Еще одна возможность, которую даст лексический анализатор — это обработка ошибок без исключений (иногда это может быть полезно). Пусть в анализаторе есть флаг, который взводится при обнаружении ошибки. Пока этот флаг сброшен, лексический анализатор работает обычным образом. Но если он взведен, вызов функции

Next

Lexeme

ltEnd

Примечание

Флагом можно сделать строковое поле, хранящее сообщение об ошибке. Пока эта строка пуста, флаг считается сброшенным, когда строка не пуста, считается, что флаг взведен. Таким образом, синтаксический анализатор формирует при необходимости сообщение об ошибке и помещает его в это поле лексического анализатора, и тот переходит в "ошибочный" режим. Так мы обеспечиваем и реализацию флага, и передачу сообщения об ошибке. В этом случае в структуре

ТLexeme

можно избавиться от поля

Pos

— позицию последней выделенной лексемы можно сделать внутренним полем лексического анализатора, и тот сам добавит номер позиции к сообщению, сформированному синтаксическим анализатором.

Теперь, познакомившись с синтаксическим анализом на практике, вернемся к теории и немного поговорим о типах грамматик и об альтернативных методах синтаксического анализа и вычисления выражений. Эти вопросы мы здесь рассмотрим только ознакомительно, а более детальное их описание можно найти в [6–8].

Грамматики языков по способу описания можно разделить на четыре типа, причем каждый следующий тип является подмножеством предыдущего.

1. Общие грамматики. Синтаксические правила в этих грамматиках имеют вид

a ::= b

а

b

2. Контекстно-зависимые грамматики. Здесь правила имеют следующий вид

a<X>b ::= acb

а

b

c

<X>

<X>

c

a

b

3. Контекстно-свободные грамматики. Это контекстно-зависимые грамматики, из которых убран контекст, т.е. правила записываются в виде

<X> ::= с

<X>

c

4. Регулярные (они же — автоматные) грамматики. Это контекстно-свободные грамматики, в которых запрещены любые формы рекурсивных определений.

Из этих определений легко сделать вывод, что в данной главе, пока мы не ввели в выражения скобки, наши грамматики относились к классу регулярных, а со скобками — к классу контекстно-свободных грамматик. Что же касается первых двух классов грамматик, то они неудобны ни для распознавания человеком, ни для написания анализаторов, поэтому данные грамматики применяются, в основном, только для описания естественных языков.

Регулярные грамматики описывают множество синтаксических правил, встречающихся в жизни, поэтому их часто применяют. Существует также альтернативный способ записи регулярной грамматики — регулярные выражения (мы их здесь рассматривать не будем). Различные библиотеки для распознавания регулярных выражений очень популярны, классы для распознавания регулярных выражений входят в .NET. Функция поиска в Delphi (меню Search/Find…. и т.п.) включает в себя возможности поиска последовательностей символов, заданных регулярным выражением (опция Regular expressions в диалоговом окне), поэтому краткое описание синтаксиса регулярных выражений можно найти в справке Delphi.

Примечание

Рекурсии в регулярных выражениях очень не хватает, когда нужно описать, например, возможность бесконечной вложенности скобок. Поэтому в некоторых анализаторах к регулярным выражениям добавляется возможность описывать бесконечное вложение структур. Эти выражения строго говоря, уже не являются регулярными, хотя их обычно продолжают так называть.

С регулярными грамматиками тесно связаны конечные автоматы. Конечный автомат — это устройство (виртуальное), с входом, на который подаются данные, набором состояний и набором правил перехода из одного состояния в другое. Правила перехода определяются символами, подаваемыми на вход, и формулируются следующим образом: "Если автомат находится в состоянии А, и на вход поступил символ X, автомат переходит в состояние В". Таким образом, выражение посимвольно передается на вход конечного автомата, и каждый символ вызывает переход автомата из одного состояния в другое (допустима ситуация, когда символ оставляет текущее состояние неизменным). Если при поступлении очередного символа автомат не находит правила, которое определяет очередной переход, считается, что на вход подан некорректный символ, т.е. выражение ошибочно. Допустимость выражения определяется также тем, в каком состоянии оказывается автомат после того, как все выражение подано на его вход. Часть состояний считается допустимыми в качестве конечного состояния, часть — недопустимыми. Если по окончании своей работы автомат оказывается в недопустимом состоянии, выражение также признается ошибочным.

Можно доказать, что для каждой регулярной грамматики можно построить конечный автомат, и, наоборот, для каждого конечного автомата можно (построить регулярную грамматику. Именно поэтому регулярные грамматики напиваются также автоматными.

Конечный автомат очень наглядно представляется с помощью графа, углами которого служат состояния автомата, ребрами — переходы между состояниями. Каждое ребро помечается символами, при поступлении на вход которых этот переход становится возможным. На рис. 4.3 показан пример такого изображения конечного автомата, соответствующего грамматике вещественного числа. Кружки с одинарной границей изображают состояния, недопустимые в качестве конечного, с двойной границей — допустимые. До начала работы автомат находится в состоянии 0, каждый следующий символ переводит его в соответствующее состояние. Конечное состояние 1 соответствует числу без дробной части и экспоненты, состояние 3 — числу с дробной частью без экспоненты, состояние 6 — числу с экспонентой.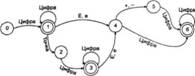

Рис. 4.3. Конечный автомат для грамматики вещественного числа

Контекстно-свободные автоматы не пригодны для распознавания контекстно-свободных грамматик с рекурсией. Для этого класса грамматик можно применить МП-автоматы (автоматы с магазинной памятью). Эти автоматы обладают стеком, и символ, поступающий на вход, не только определяет правило перехода, но и может быть сохранен в стеке, а правила перехода могут учитывать не только поступивший на вход символ, но и символ, лежащий на вершине стека. Если символ на вершине стека учитывается правилом, при применении этого правила символ извлекается из стека.

Главное достоинство МП-автоматов по сравнению с методом рекурсивного спуска (так называется метод построения синтаксического анализатора, который мы использовали) является то, что код автомата универсален и может быть применен к любому набору правил. Таким образом, появляется возможность создавать анализаторы, правила для которых хранятся, например, во внешнем файле или в базе данных, и грамматика может быть изменена без перекомпиляции анализатора. Недостатки МП-автоматов — малая наглядность кода и медленная работа из-за возможности захода в тупиковые ветки. Поэтому метод рекурсивного спуска применяется всегда, когда нет нужды менять грамматику во время работы программы.

В книге [6] описана интересная разновидность МП-автоматов — табличный анализатор, который в некоторых случаях может оказаться предпочтительнее метода рекурсивного спуска.

Арифметические выражения, которые мы разбирали в этой главе, записаны в привычной нам инфиксной форме, т.е. когда знак бинарной операции ставится между операндами. Кроме инфиксной, существует также префиксная и постфиксная формы записи выражения, в которых оператор записывается, соответственно, перед и после операндов. Например выражение "2+2" в префиксной форме запишется как "+2 2", в постфиксной — "2 2+". Префиксная форма называется польской записью, постфиксная — польской инверсной записью (в честь польского математика Яна Лукасевича, который разработал эти формы записи).

Достоинства префиксной и постфиксной форм записи — отсутствие скобок и одинаковый приоритет всех операций. Например, выражение "2+(2*2)" в постфиксной записи имеет вид "2 2 * 2 +", а выражение "(2+2)*2", соответственно, "2 2 + 2 *". Операции всегда выполняются в том порядке, в котором они следуют в выражении.

Примечание

Префиксная запись имеет много общего принятым обозначением функций. Представим, что в некотором языке программирования нет встроенной инфиксной операции сложения, но есть функция +, которая принимает два аргумента и возвращает их сумму и аналогичные функции для других бинарных операторов. В привычной форме записи функций, когда аргументы заключаются в скобки, приведенное выражение будет выглядеть так "

+(2, +(2, 2)

". Теперь достаточно убрать из него скобки и запятые, чтобы получить префиксную запись выражения в классическом виде. Постфиксная запись получается из функциональной подобным образом, надо только ввести правило, что имя функции пишется не перед списком аргументов, а после него.

По своим выразительным возможностям постфиксная и префиксная записи равноценны, но при вычислении выражения, заданного префиксной записью, требуется рекурсивный алгоритм, а при вычислении выражения в постфиксной записи достаточно линейного алгоритма и стека, поэтому чаще встречается постфиксная форма. Алгоритм вычисления постфиксного выражения очень прост. Если очередная лексема — это число, кладем его в стек. Если очередная лексема — бинарный оператор, выталкиваем из стека два верхних значения, применяем к ним операцию и результат помещаем обратно в стек. Алгоритм легко обобщается на операторы с любым количеством операндов: соответствующая операция выталкивает из стека не два, а нужное ей число параметров. Функция от N аргументов рассматривается как операция, применяющаяся к N операндам.

Простота постфиксной записи делает ее очень привлекательной для низкоуровневого программирования. Метолом рекурсивного спуска достаточно легко создать код, переводящий выражение из инфиксной формы в постфиксную, а затем вычислить выражение уже в постфиксной форме. В простейшем случае такой промежуточный перевод только замедляет вычисления, и поэтому не используется, но иногда (например, при многократном вычислении одного выражения) перевод в постфиксную запись может сильно ускорить вычисления, тем более что выражение в постфиксной форме можно хранить не в виде строки, а в виде списка лексем, что еще больше ускорит его вычисление. В частности, код для стековой Java-машины, вычисляющий выражения, по сути эквивалентен постфиксной записи выражения.

Конечно, синтаксический анализ — вещь непростая, и здесь мы рассмотрели только самые его основы. За рамками книги остались атрибутивные грамматики, семантические деревья, генераторы языков и многое другое. Этим сложным вопросам посвящены специализированные книги. Долгое время ощущалась нехватка книг по данной тематике, но за последние два года вышли сразу три книги ([6–8]), посвященные созданию трансляторов. В этих книгах детально разбираются фундаментальные основы теории и даются примеры ее использования. Особенно стоит отметить книгу [6], в которой описан очень интересный язык программирования — Оберон-2, созданный при участии Никлауса Вирта; в нем развиваются идеи, заложенные Виртом в Паскаль. Ряд идей, предложенных при создании различных версий Оберона, уже позаимствованы другими языками (Java, C#, Ада), и еще многие ждут своего часа, поэтому программисту следует хотя бы ознакомительно изучить Оберон, чтобы понимать, в каком направлении может пойти развитие языков программирования.

В качестве источника полезных сведений можно также посоветовать книги, посвященные не столько теории разработки языков программирования, сколько истории их развития, например, [5, 9]. Теория синтаксического и семантического анализа в них изложена относительно неглубоко, но тесная связь изложения с практическими примерами позволяет существенно расширить кругозор в данной области. Особенно рекомендуем [5]. Книга [9] содержит больше сведений, но написана более тяжелым языком, а ее авторы крайне предвзято относятся к Паскалю, ставя ему в вину его достоинства и упрекая в несуществующих недостатках. Тем не менее эту книгу тоже следует прочитать.