|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
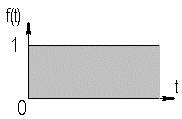
2. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА НА ТРАНЗИСТОРАХ2.1. Классификация усилительных устройствОдна из основных функций, реализуемых аналоговыми устройствами, — усиление. Поэтому в курсе АЭУ особое внимание уделяется усилительным устройствам (УУ). УУ называется устройство, предназначенное для повышения (усиления) мощности входного сигнала. Усиление происходит с помощью активных элементов за счет потребления мощности от источника питания. В УУ входной сигнал лишь управляет передачей энергии источника питания в нагрузку. В качестве активных элементов чаще всего применяются транзисторы, такие УУ принято называть полупроводниковыми, или транзисторными. УУ принято классифицировать по ряду признаков: ▶ по характеру усиливаемых сигналов — УУ непрерывных (гармонических) и УУ импульсных сигналов; ▶ по диапазону рабочих частот — УУ постоянного тока (fн=0 Гц) и УУ переменного тока. В свою очередь, УУ переменного тока в учебной литературе (и в данном пособии) подразделяются на: ◆ усилители звуковых частот (от 20 до 20000 Гц) или низкочастотные усилители; ◆ усилители высоких частот (ВЧ) (fв до 300 МГц); ◆ усилители сверхвысоких частот (СВЧ) (fв›300 МГц). В специальной литературе принято классифицировать УУ переменного тока по диапазону рабочих частот согласно таблице 1.1. Таблица 1.1 - Границы частотных диапазонов
Кроме того, УУ ВЧ и СВЧ диапазонов подразделяются на: • узкополосные (fв/fн<2, (fв–fн)≪f0); где f0 — средняя частота рабочего диапазона УУ; • широкополосные (fв/fн>2). ▶ импульсные усилители классифицируются по длительности усиливаемых импульсов на микро-, нано- и пикосекундные; ▶ по типу активных элементов УУ подразделяются на ламповые, транзисторные, квантовые и др.; ▶ по функциональному назначению УУ подразделяются на усилители напряжения, тока и мощности; ▶ по назначению УУ подразделяются на измерительные, телевизионные и т.д. Кроме рассмотренных основных признаков УУ могут классифицироваться по ряду дополнительных признаков — числу каскадов, типу питания, конструктивному исполнению и т.д. 2.2. Основные технические показатели и характеристики УУ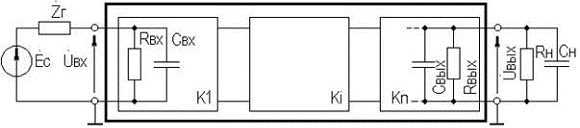 Рисунок 2.1. Структурная схема усилителя Технические показатели УУ представляют собой количественную оценку его свойств. К техническим показателям относятся (рис. 2.1): ◆ входное сопротивление Zвх. Чаще всего Zвх носит емкостной характер; ◆ выходное сопротивление Zвых. Чаще всего Zвых носит так же емкостной характер; ◆ коэффициенты передачи: • по напряжению 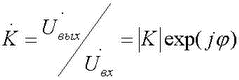 где φ — фазовый сдвиг между входным и выходным сигналами. Значение |K| на средних частотах рабочего диапазона УУ, обозначаемого как K0, называют коэффициентом усиления. В логарифмических единицах: K0,dB = 20lgK0. Для n-каскадных УУ (каскады включены последовательно): KΣ = K1 * K2 * … Kn, KΣ,dB = K1,dB + K2,dB + … + Kn,dB; • по току 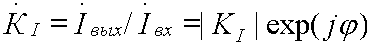 Для n-каскадных усилителей KIΣ в относительных и логарифмических единицах определяются аналогично KΣ. • по мощности KP: KP = Pвых/Pвх. Для n-каскадных усилителей KPΣ в относительных и логарифмических единицах определяются аналогично KΣ, только KP,dB = 20lgKp. • сквозные коэффициенты, например, сквозной коэффициент передачи по напряжению 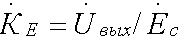 где Ec — ЭДС источника сигнала. ◆ коэффициент полезного действия: КПД = Pпот/P0, где Pпот — максимальная выходная мощность усилителя; P0 — мощность, потребляемая от источника питания. Характеристики УУ служат для оценки искажения сигнала. Искажения — это отклонения формы выходного сигнала от формы входного. В зависимости от происхождения они подразделяются на: ◆ искажения частотные, вызываемые неодинаковым усилением усилителя на разных частотах. Частотные искажения создаются LC элементами, поэтому они носят линейный характер. Вносимые усилителем частотные искажения оценивают по амплитудно-частотной характеристике (АЧХ) и по фазочастотной характеристике (ФЧХ). АЧХ называется зависимость модуля коэффициента передачи от частоты. Часто используют нормированную АЧХ, представленную на рис. 2.2. 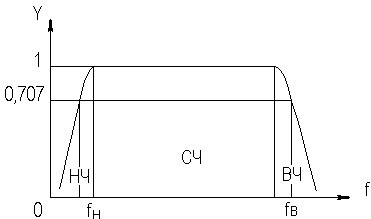 Рисунок 2.2 АЧХ УУ Здесь Y — относительный (нормированный) коэффициент усиления: Y = |K|/K0, Y,dB = 20lgY. Структура выражений для n-каскадного усилителя в относительных и логарифмических единицах в точности совпадает с выражениями для K и получается из последних путем замены K на Y. Количественно частотные искажения оцениваются коэффициентом частотных искажений M: M = 1/Y = K0/|K|, M,dB = 20lgM. Структура выражений для n-каскадного усилителя в относительных и логарифмических единицах также в точности совпадает с выражениями для K и получается из последних путем замены K на M. По АЧХ и допустимой величине частотных искажений определяют нижнюю fн и верхнюю fв граничные частоты, полосу рабочих частот Δf, равную: Δf = fв – fн. ◆ искажения фазовые, вызываемые различным фазовым сдвигом различных по частоте составляющих спектра сигнала. Фазовые искажения создаются LC элементами, поэтому они носят линейный характер. 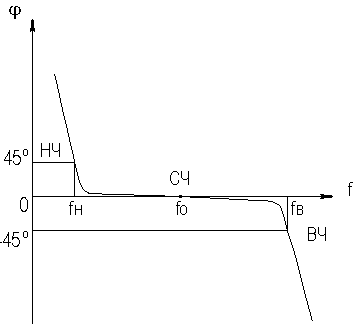 Рисунок 2.3 ФЧХ УУ Зависимость угла сдвига по фазе между входным и выходным сигналами от частоты оценивается по ФЧХ, для резистивного каскада имеющей вид, представленный на рис. 2.3. В импульсных усилителях форма выходного напряжения зависит от переходных процессов в цепях, содержащих LC элементы. Для оценки линейных искажений, называемых в ИУ переходными, пользуются переходной характеристикой (ПХ). ПХ усилителя это зависимость мгновенного значения напряжения (тока) на выходе от времени Uвых=f(t) при подаче на вход единичного скачкообразного изменения напряжения (тока) (сигнала типа единичной функции). 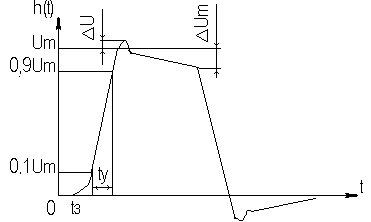 Рисунок 2.4. ПХ УУ ◆ переходные искажения измеряют при подаче на вход идеального прямоугольного импульса. Они разделяются на искажения фронта и искажения плоской вершины импульса (рис. 2.4). ◆ искажения фронта характеризуются: • временем установления tу, т.е. временем нарастания амплитуды импульса от 0,1Um до 0,9Um; • выбросом фронта импульса δ, определяемым отношением амплитуды выброса ΔU к амплитуде установившегося режима Um; • временем запаздывания tз относительно входного сигнала по уровню 0,1Um. ◆ Искажения плоской вершины импульса Δ характеризуется величиной спада напряжения ΔUm за время длительности импульса: Δ,% = ΔUm/Um·100%. Для n-каскадных некорректированных УУ (каскады включены последовательно) результирующее время установления фронта и спад плоской вершины импульса можно оценить следующим образом: 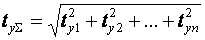 ΔΣ = Δ1 + Δ2 + … +Δn. АЧХ и ПХ отражают одни и те же физические процессы в различной форме (частотной и временной). Связь частотных и временных искажений иллюстрируется рис. 2.5. 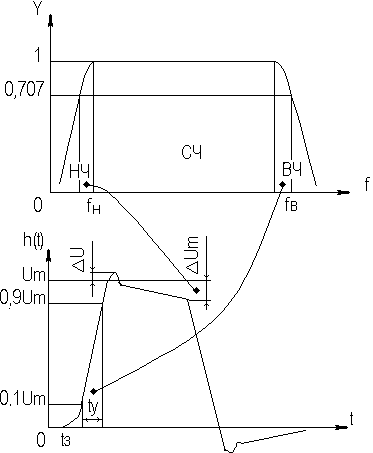 Рисунок 2.5. Связь АЧХ и ПХ ◆ Нелинейные искажения (искажения формы выходного сигнала) вызываются нелинейностью характеристик усилительных элементов. Количественно нелинейные искажения гармонического сигнала оцениваются коэффициентом гармоник Kг, который представляет собой отношение действующего значения напряжения (тока, мощности) высших гармоник, появившихся в результате нелинейных искажений, к напряжению (току, мощности) основной частоты (первой гармоники) при подаче на вход гармонического колебания основной частоты (при частотно-независимой нагрузке): 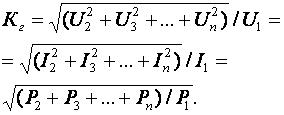 Для n-каскадных УУ (каскады включены последовательно): 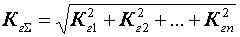 Кроме Kг в усилителях многоканальной связи нелинейность оценивается затуханием соответствующей гармонической составляющей, (например, второй): a2 = 20lg(U1/U2). ◆ Собственные помехи УУ: фон, наводки и шумы. Остановимся на тепловых внутренних шумах усилителя ввиду принципиальной невозможности их полного устранения. Любое резистивное сопротивление R (например, внутреннее сопротивление источника сигнала Rг) создает в полосе частот Δf тепловой шум, среднеквадратичная ЭДС которого определяется формулой Найквиста: Ē²ш = 4kTRΔf. Где k — постоянная Больцмана; T — абсолютная температура сопротивления. Мерой оценки шумовых свойств УУ является коэффициент шума F, равный отношению мощностей сигнала и шума на входе УУ к отношению мощностей сигнала и шума на выходе УУ: F = (Pс/Pш)вх/(Pс/PΣш)вых F,dB = 10lgF В диапазоне СВЧ находит применение оценка шумовых свойств УУ посредством определения шумовой температуры системы Tс: Tс = T0(F – 1), где T0 — стандартная шумовая температура, T0 = 290°K (рекомендация МЭК). Для многокаскадных УУ (каскады включены последовательно): FΣ = F1 + (F2–1)/Kp1 + (F3–1)/Kp1Kp2 + … TсΣ = Tс1 + (Tс2–1)/Kp1 + (Tс3–1)/Kp1Kp2 + … где Kp1, Kp2 и т.д. — номинальные коэффициенты усиления по мощности каскадов усилителя. ◆ Амплитудная характеристика и динамический диапазон УУ. Амплитудная характеристика усилителя представлена на рис. 2.6. 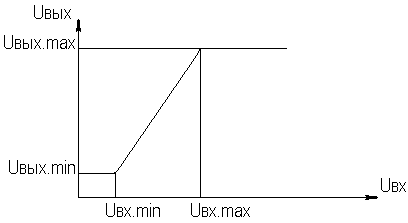 Рисунок 2.6. АХ УУ Динамическим диапазоном входного сигнала усилителя Dвх называют отношение Uвх.max (при заданном уровне нелинейных искажений) к Uвх.min (при заданном отношении сигнал/шум на входе): Dвх = Uвх.max/Uвх.min Dвх,dB = 20lgDвх В зависимости от назначения УУ возможна оценка динамического диапазона по выходному сигналу, гармоническим и комбинационным составляющим и др. Некоторые УУ (УПТ, ОУ и т.д.) могут характеризоваться другими специфическими показателями, которые будут рассмотрены по мере необходимости. 2.3. Методы анализа линейных усилительных каскадов в частотной областиБольшинство соотношений, приведенных в данном пособии, получено на основе обобщенного метода узловых потенциалов (ОМУП) [3]. При использовании ОМУП схема в целом заменяется матрицей эквивалентных проводимостей, отображающей как конфигурацию, так и свойства некоторой линейной схемы, аппроксимирующей реальную схему. Матрица проводимостей составляется на основе формальных правил [3]. При этом усилительные элементы представляются в виде четырехполюсников (подсхем), описываемых эквивалентными Y-параметрами. Выбор Y-параметров активных элементов в качестве основных обусловлен их хорошей стыковкой с выбранным методом анализа. При наличии других параметров активных элементов, возможен их пересчет в Y-параметры [3]. При использовании ОМУП анализ состоит в следующем: ◆ составляют определенную матрицу проводимостей схемы [3]; ◆ вычисляют определитель Δ и соответствующие алгебраические дополнения Δij; ◆ определяют (при необходимости) эквивалентные четырехполюсные Y-параметры схемы; ◆ определяют вторичные параметры усилительного каскада. Так как обычно УУ имеют общий узел между входом и выходом, то, согласно [3], их первичные и вторичные параметры определяются следующим образом: Yij = Δij / Δii,jj, Zij = Δij / Δ, Kij = Δij / Δii. где i, j — номера узлов, между которыми определяются параметры; Δii,jj — двойное алгебраическое дополнение. По практическим выражениям, получаемым путем упрощения вышеприведенных выражений, вычисляют необходимые параметры усилительного каскада, например: Yвх = Gвх + jωCвх, Yвых = Gвых + jωCвых, K(jω) = K0/(1 + jωτ). где t — постоянная времени цепи, Gвх, Gвых — низкочастотные значения входной и выходной проводимости. Полученные соотношения позволяют с приемлемой точностью проводить эскизный расчет усилительных каскадов. Результаты эскизного расчета могут быть использованы в качестве исходных при проведении машинного моделирования и оптимизации. Методы машинного расчета УУ приведены в [4]. 2.4. Активные элементы УУ2.4.1. Биполярные транзисторыБиполярными транзисторами (БТ) называют полупроводниковые приборы с двумя (или более) взаимодействующими p-n-переходами и тремя (или более) выводами, усилительные свойства которых обусловлены явлениями инжекции и экстракции не основных носителей заряда. Для определения малосигнальных Y-параметров БТ используют их эквивалентные схемы. Из множества разнообразных эквивалентных схем наиболее точно физическую структуру БТ отражает малосигнальная физическая Т-образная схема. Для целей эскизного проектирования, при использовании транзисторов до (0,2...0,3) fT (fT — граничная частота усиления транзистора с ОЭ) возможно использование упрощенных эквивалентных моделей транзисторов, параметры элементов эквивалентных схем которых легко определяются на основе справочных данных. Упрощенная эквивалентная схема биполярного транзистора приведена на рис. 2.7. 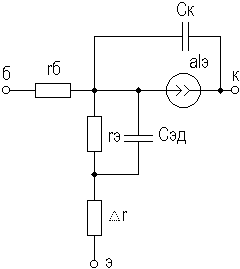 Рисунок 2.7. Эквивалентная схема биполярного транзистора Параметры элементов определяются на основе справочных данных следующим образом: ◆ объемное сопротивление базы rб=τос/Cк, где τос — постоянная времени цепи внутренней обратной связи в транзисторе на ВЧ; ◆ активное сопротивление эмиттера rэ=25,6/Iэ, при Iэ в миллиамперах rэ получается в омах; ◆ диффузионная емкость эмиттера Cэд=1/(2πfTrэ), где fT — граничная частота усиления по току транзистора с ОЭ, fT=|h21э|·fизм ; ◆ коэффициент усиления тока базы для транзистора с ОБ α=H21э/[(1+H21э)·(1+jf/fT)], где H21э — низкочастотное значение коэффициента передачи по току транзистора с ОЭ. ◆ Δr =(0,5…1,5) Ом; Таким образом, параметры эквивалентной схемы биполярного транзистора полностью определяются справочными данными H21э,fT(|h21э|·fизм),Cк,tос(rб) и режимом работы. Следует учитывать известную зависимость Cк от напряжения коллектор-эмиттер Uкэ: 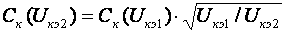 По известной эквивалентной схеме не представляет особого труда, пользуясь методикой, изложенной в разделе 2.3, получить приближенные выражения для низкочастотных значений Y-параметров биполярного транзистора, включенного по схеме с ОЭ: Y11эНЧ = g ≈ 1/(rб + (1 + H21э)(rэ + Δr)), Y21эНЧ = S0 ≈ H21эgэ, Y12эНЧ ≈ 0, Y22эНЧ ≈ 0. Частотную зависимость Y11э и Y21э при анализе усилительного каскада в области ВЧ определяют, соответственно, посредством определения входной динамической емкости Cвх.дин и постоянной времени транзистора τ. Выражения для расчета низкочастотных Y-параметров для других схем включения транзистора получают следующим образом: ◆ дополняют матрицу исходных Y-параметров Yэ до неопределенной Yн, а именно, если 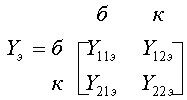 то 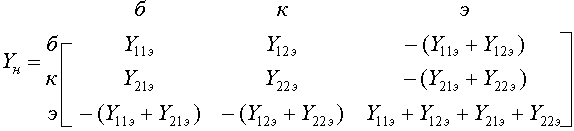 ◆ вычеркивают строку и столбец, соответствующие общему узлу схемы (б для ОБ, к для ОК), получая матрицу Y-параметров для конкретной схемы включения транзистора. 2.4.2. Полевые транзисторыПолевыми транзисторами (ПТ) называются полупроводниковые усилительные приборы, в основе работы которых используются подвижные носители зарядов одного типа — либо электроны, либо дырки. Наиболее характерной чертой ПТ является высокое входное сопротивление, поэтому они управляются напряжением, а не током, как БТ. 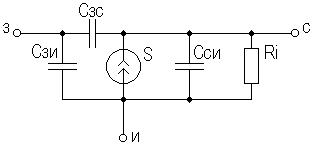 Рисунок 2.8. Эквивалентная схема ПТ Определяются малосигнальные Y-параметры ПТ по его эквивалентной схеме. Для целей эскизного проектирования можно использовать упрощенный вариант малосигнальной эквивалентной схемы ПТ, представленный на рис.2.8. Данная схема с удовлетворительной для эскизного проектирования точностью аппроксимирует усилительные свойства ПТ независимо от его типа, параметры ее элементов находятся из справочных данных Выражения для эквивалентных Y-параметров ПТ, включенного по схеме с ОИ определяют по методике п. 2.3: Y11з = jωCзи, Y12з = jωCзс, Y21и = S0ejωτ, Y22и = gi + jωCси. Где з, с, и соответственно затвор, сток и исток ПТ; τ — время пролета носителей, τ=Cзи/S0. Граничную частоту единичного усиления ПТ fT можно оценить по формуле: fT = 1/2πτ. Анализ полученных выражений для эквивалентных Y-параметров ПТ, проведенный с учетом конкретных численных значений справочных параметров, позволяет сделать вывод о незначительной зависимости крутизны от частоты, что позволяет в эскизных расчетах использовать ее низкочастотное значение S0. При отсутствии справочных данных о величине внутренней проводимости ПТ gi, в эскизных расчетах можно принимать gi≈0 ввиду ее относительной малости. Пересчет эквивалентных Y-параметров для других схем включения ПТ осуществляется по тем же правилам, что и для БТ. 2.5. Усилительный каскад на биполярном транзисторе с ОЭСреди многочисленных вариантов усилительных каскадов на БТ самое широкое применение находит каскад с ОЭ, имеющий максимальный коэффициент передачи по мощности KP, вариант схемы которого приведен на рисунке 2.9. Если входного сигнала нет, то каскад работает в режиме покоя. С помощью резистора Rб задается ток покоя Iб0=(Eк–Uбэ0)/Rб. Ток покоя коллектора Iк0=H21эIб0. Напряжение коллектор-эмиттер покоя Uк0=Eк–Iк0Rк. Отметим, что в режиме покоя напряжение Uбэ0 составляет десятки и сотни мВ (обычно 0,5…0,8 В). При подаче на вход положительной полуволны синусоидального сигнала будет возрастать ток базы, а, следовательно, и ток коллектора. В результате напряжение на Rк возрастет, а напряжение на коллекторе уменьшится, т.е. произойдет формирование отрицательной полуволны выходного напряжения. Таким образом, каскад с ОЭ осуществляет инверсию фазы входного сигнала на 180°. 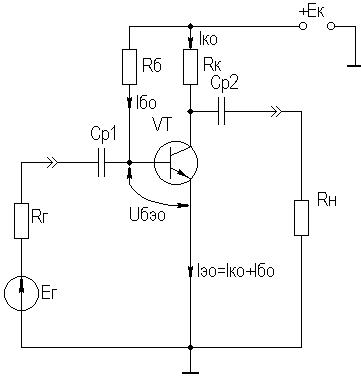 Рисунок 2.9. Простой усилительный каскад с ОЭ Графически проиллюстрировать работу каскада с ОЭ можно, используя входные и выходные статические характеристики БТ, путем построения его динамических характеристик (ДХ) [5,6]. Вследствие слабой зависимости входной проводимости транзистора g от величины нагрузки, входные статические и динамические характеристики практически совпадают. Выходные ДХ — это прямые линии, которые в координатах Iк, Uкэ соответствуют уравнениям, выражающим зависимости между постоянными и переменными значениями токов и напряжений на нагрузках каскада по постоянному и переменному току. Процесс построения выходных динамических характеристик (нагрузочных прямых по постоянному — R=, переменному — R≈ току) понятен из рисунка 2.10. Следует отметить, что простое построение ДХ возможно только при активной нагрузке, т.е. в области СЧ АЧХ (см. рис.2.2), в областях НЧ и ВЧ нагрузочные прямые трансформируются в сложные кривые. Построение ДХ и их использование для графического расчета усилительного каскада подробно описано в [5,6]. 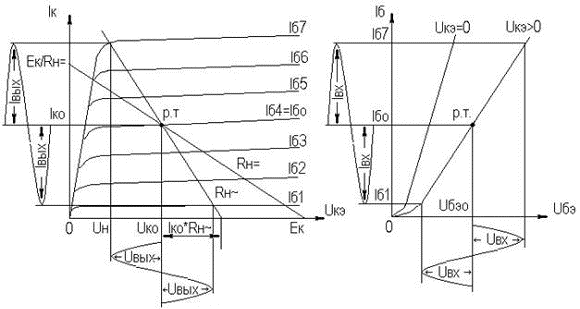 Рисунок 2.10. Динамические характеристики каскада с ОЭ Нагрузки рассматриваемого каскада по постоянному и переменному току определяются как: R= = Rк; R≈ = Rк ∥ Rн. Координаты рабочей точки (Uк0, Iк0, Uбэ0, Iб0) для малосигнальных усилительных каскадов выбирают на линейных участках входной и выходной ВАХ БТ, используя в малосигнальных усилительных каскадах так называемый режим (класс) усиления А. Другие режимы работы каскадов чаще используются в усилителях мощности, и будут рассмотрены в соответствующем разделе. При отсутствии в справочных данных ВАХ БТ, координаты рабочей точки могут быть определены аналитическим путем (см. рисунок 2.10): Uк0 = Uвых + Uн, где Uн — напряжение нелинейного участка выходных статических ВАХ транзистора, Uн=1…2 В; Iк0 ≥ Uвых / R≈, Iб0 = Iк0 / H21э, Uбэ0 = 0,6…0,8 В (для кремниевых транзисторов), Uбэ0 = 0,4…0,6 В (для германиевых транзисторов). Если для малосигнальных каскадов в результате расчета по вышеприведенным формулам значения Uк0 и Iк0 окажутся, соответственно, меньше 2 В и 1 мА, то, если не предъявляются дополнительные требования к экономичности каскада, рекомендуется брать те значения координат рабочей точки, при которых приводятся справочные данные и гарантируются оптимальные частотные свойства транзистора. Для расчета параметров усилительного каскада по переменному току удобно использовать методику, описанную в разделе 2.3, а БТ представлять моделью, предложенной в разделе 2.4.1. Полная электрическая схема усилительного каскада с ОЭ приведена на рис. 2.11. 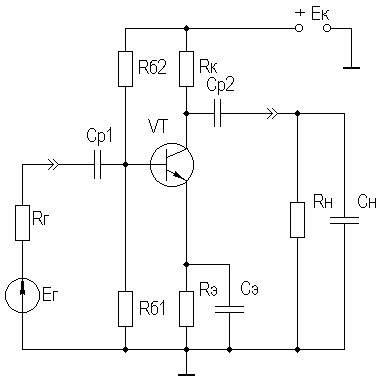 Рисунок 2.11. Усилительный каскад со ОЭ В отличие от ранее рассмотренного каскада (рис.2.9) здесь применена эмиттерная схема термостабилизации (Rб1, Rб2, Rэ), обеспечивающая лучшую стабильность режима покоя, принцип ее работы будет рассмотрен далее. Конденсатор Cэ необходим для шунтирования Rэ с целью соединения эмиттера транзистора с общим проводом на частотах сигнала (устранения обратной связи на частотах сигнала, вид и характер этой связи будет рассмотрен в соответствующем разделе). Приведем эквивалентную схему каскада для частот сигнала (рис. 2.12). 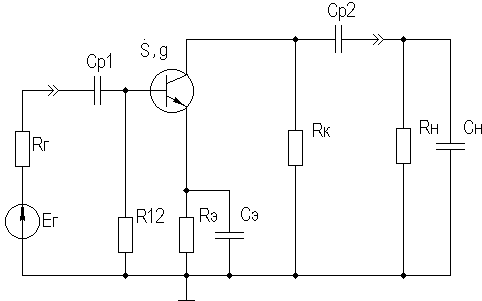 Рисунок 2.12. Схема каскада с ОЭ для частот сигнала С целью упрощения анализа каскада выделяют на АЧХ области НЧ, СЧ и ВЧ (см. рис. 2.2), и проводят анализ отдельно для каждой частотной области. Эквивалентная схема каскада в области СЧ приведена на рисунке 2.13. 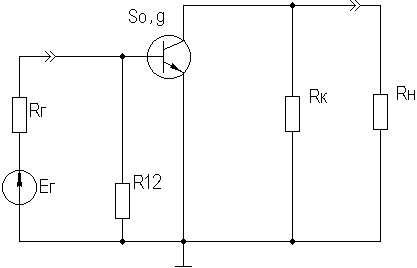 Рисунок 2.13. Схема каскада с ОЭ в области СЧ Как видно, эта схема не содержит реактивных элементов, т.к. в области СЧ влиянием на АЧХ разделительных (Cp1, Cp2) и блокировочных (Cэ) емкостей уже можно пренебречь, а влияние инерционности БТ и Cн еще незначительно. Проведя анализ схемы, найдем, что K0 = S0Rэкв, где Rэкв ≈ Rк ∥ Rн; gвх ≈ g + G12, где G12 = 1/R12 = 1/(Rб1 ∥ Rб2); gвых ≈ g = 1/Rк. Эти соотношения получены в предположении, что низкочастотное значение внутренней проводимости транзистора g22э много меньше gк и gн. Это условие (если не будет оговорено особо) будет действовать и при дальнейшем анализе усилительных каскадов на БТ. Такое допущение справедливо потому, что БТ является токовым прибором и особенно эффективен при работе на низкоомную нагрузку. Эквивалентная схема каскада в области ВЧ приведена на рисунке 2.14. 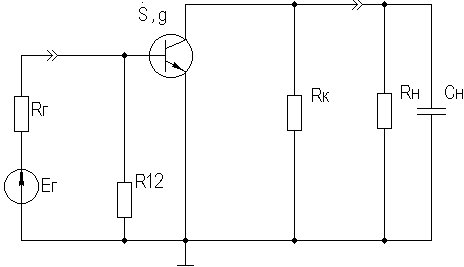 Рисунок 2.14. Схема каскада с ОЭ в области ВЧ Поведение АЧХ в этой области определяется влиянием инерционности транзистора и емкости Cн. Проведя анализ согласно методике раздела 2.4, получим выражение для коэффициента передачи каскада в области ВЧ: 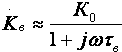 где τв — постоянная времени каскада в области ВЧ. Постоянную времени каскада для удобства анализа представим так: τв = τ + τ1 + τ2, где τ — постоянная времени транзистора ( 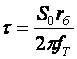 τ1 — постоянная времени выходной цепи транзистора, τ1 = S0CкrбRэкв; τ2 — постоянная времени нагрузки, τ2 = CнRэкв. Входную проводимость представим в виде: 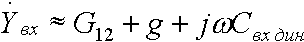 где Cвх.дин — входная динамическая емкость каскада, Cвх.дин ≈ Cэд + (1 + K0)Cк = τ/rб + (1 + K0)Cк. Выходная проводимость определится как 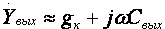 где Cвых — выходная емкость каскада, Cвых=CкS0rб. Выражения для относительного коэффициента передачи Yв и коэффициента частотных искажений Mв в комментариях не нуждаются: 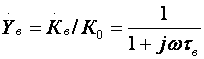 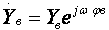 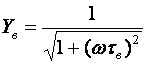 φв = –arctg ωτв, Mв = 1/Yв По приведенным выражениям строится АЧХ и ФЧХ каскада в области ВЧ. Связь коэффициента частотных искажений Mв и fв выражается как 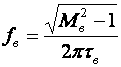 В n-каскадном усилителе с одинаковыми каскадами наблюдается эффект сужения полосы рабочих частот, который можно скомпенсировать увеличением верхней граничной частоты каскадов fвi до 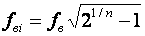 Эквивалентная схема каскада в области НЧ приведена на рисунке 2.15. 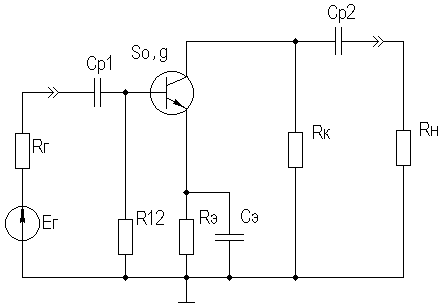 Рисунок 2.15. Схема каскада с ОЭ в области НЧ Поведение АЧХ в этой области определяется влиянием разделительных (Cр1, Cр2) и блокировочных (Cэ) емкостей. Влияние этих емкостей на коэффициент частотных искажений в области НЧ Mн каскада можно определить отдельно, используя принцип суперпозиции. Общий коэффициент частотных искажений в области НЧ определится как 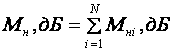 где N — число цепей формирующих АЧХ в области НЧ. Рассмотрим влияние Cр2 на АЧХ каскада. Проведя анализ согласно методике раздела 2.4, получим выражение для коэффициента передачи в области НЧ: Kн = K0/(1 + 1/jωτн), где τн — постоянная времени разделительной цепи в области НЧ. Постоянная времени разделительных цепей в общем случае может быть определена по формуле τн = Cр(RЛ + RП), где RЛ — эквивалентное сопротивление, стоящее слева от Cр (обычно это выходное сопротивление предыдущего каскада или внутреннее сопротивление источника сигнала), RП — эквивалентное сопротивление, стоящее справа от Cр (обычно это входное сопротивление следующего каскада или сопротивление нагрузки). Для рассматриваемой цепи постоянная времени равна: τн2 = Cр2(Rк + Rн). Выражения для относительного коэффициента передачи и коэффициента частотных искажений в области НЧ таковы: 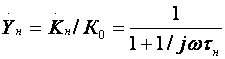 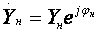 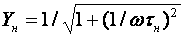 φн = –arctg ωτн, Mн = 1/Yвн и в комментариях не нуждаются. По этим выражениям оценивается влияние конкретной цепи на АЧХ и ФЧХ каскада в области НЧ. Связь между коэффициентом частотных искажений и нижней граничной частотой выражается формулой 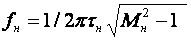 Аналогичным образом учитывается влияние других разделительных и блокировочных цепей, только для блокировочной эмиттерной цепи постоянная времени приблизительно оценивается величиной τнэ≈Cэ/S0 т.к. сопротивление БТ со стороны эмиттера приблизительно равно 1/S0 (см. подраздел 2.4.1), а влиянием Rэ в большинстве случаев можно пренебречь, т.к. обычно 1/S0<<Rэ. Результирующую АЧХ и ФЧХ каскада в области НЧ можно построить, используя уже упоминавшийся принцип суперпозиции. В n-каскадном усилителе с одинаковыми каскадами наблюдается эффект сужения полосы рабочих частот, который в области НЧ можно скомпенсировать уменьшением нижней граничной частоты каскадов до 2.6. Термостабилизация режима каскада на биполярном транзистореПараметры БТ в значительной мере подвержены влиянию внешних факторов (температуры, радиации и др.). В то же время, одним из основных параметров усилительного каскада является его стабильность. Прежде всего, важно, чтобы в усилителе обеспечивался стабильный режим покоя. Проанализируем вопрос влияния температуры на стабильность режима покоя БТ, конкретно — Iк0. Существуют три основных фактора, влияющих на изменении Iк0 под действием температуры: при увеличении температуры, во-первых, увеличивается напряжение Uбэ0, во-вторых, обратный ток коллекторного перехода Iкбо, и, в третьих, возрастает коэффициент H21э. 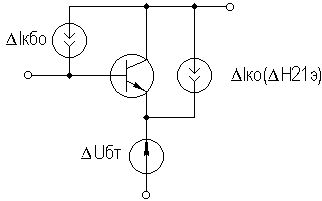 Рисунок 2.16. Тепловая модель БТ Для анализа реальный транзистор можно представить в виде идеального, у которого параметры не зависят от температуры, а температурную зависимость смоделировать включением внешних источников напряжения и тока (рисунок 2.16). Рассмотрим влияние этих факторов на приращение тока коллектора ΔIк0. Начнем с влияния изменения Uбэ0, вызванного тепловым смещением проходных характеристик Iк=f(Uбэ), обозначив при этом приращение тока коллектора как ΔIк01: ΔIк01 = S0·ΔUбТ , где ΔUбТ — приращение напряжения Uбэ0, равное: ΔUбТ = |εT|·ΔТ, где εT — температурный коэффициент напряжения (ТКН), εT ≈ –3мВ/град., ΔТ — разность между температурой коллекторного перехода перехода Tпер и справочным значением этой температуры Tспр (обычно 25°C): ΔТ = Tпер – Tспр, Tпер = Tсред + PкRT, где Pк и RT соответственно, мощность, рассеиваемая на коллекторном переходе в статическом режиме, и тепловое сопротивление “переход-среда”: Pк = Iк0·Uк0, 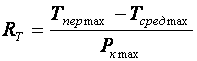 Ориентировочное значение теплового сопротивления зависит от конструкции корпуса транзистора и обычно для транзисторов малой и средней мощности лежит в следующих пределах: RT = (0,1…0,5) град./мВт. Меньшее тепловое сопротивление имеют керамические и металлические корпуса, большее — пластмассовые. Отметим, что ΔIк01 берется положительным, хотя εT имеет знак минус, это поясняется на рисунке 2.17. 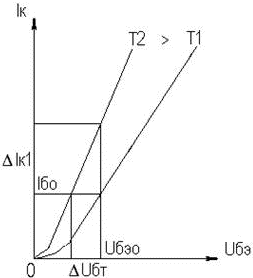 Рисунок 2.17. Тепловое смещение проходных характеристик БТ Определяем приращение тока коллектора ΔIк02, вызванного изменением обратного (неуправляемого) тока коллектора ΔIкбо: ΔIк02 = ΔIкбо·(H21э + 1), где приращение обратного тока ΔIкбо равно: ΔIкбо = Iкбо(Tспр)·[exp(αΔT) – 1], где α — коэффициент показателя, для кремниевых транзисторов α=0,13. Следует заметить, что значение Iкбо, приводимое в справочной литературе, особенно для транзисторов средней и большой мощности, представляет собой сумму тепловой составляющей и поверхностного тока утечки, последний может быть на два порядка больше тепловой составляющей, и он практически не зависит от температуры. Следовательно, при определении ΔIк02 следует пользоваться приводимыми в справочниках температурными зависимостями Iкбо, либо уменьшать справочное значение Iкбо примерно на два порядка (обычно Iкбо для кремниевых транзисторов составляет порядка (n·10-7…n·10-6) А, и порядка (n·10-6…n·10-5) А для германиевых, n=(1…9). Приращение коллекторного тока, вызванного изменением H21э, определяется соотношением: ΔIк03 = H21э·(Iкбо + Iб0), где ΔH21э = kT·H21э·ΔT, kT ≈ 0,005 отн. ед./град. Полагая, что все факторы действуют независимо друг от друга, запишем: ΔIк0 = ΔIк01 + ΔIк02 + ΔIк03. Для повышения термостабильности каскада применяют специальные схемы питания и термостабилизации. Эффективность таких схем коэффициентом термостабильности, который в общем виде представляется как: ST = ΔIк0 стаб/ΔIк0. Учитывая различный вклад составляющих ΔIк0, разное влияние на них элементов схем термостабилизации, вводят для каждой составляющей свой коэффициент термостабильности, получая выражения для термостабилизированного каскада: ΔIк0 стаб = ST1ΔIк01+ ST2ΔIк02 + ST3ΔIк03. Обычно ST2≈ST3, что обусловлено одинаковым влиянием на ΔIк02 и ΔIк03 элементов схем термостабилизации: ΔIк0 стаб = ST1ΔIк01+ ST2(ΔIк02 + ΔIк03). Полученная формула может быть использована для определения ΔIк0 усилительного каскада при любой схеме включения в нем БТ. Рассмотрим основные схемы питания и термостабилизации БТ. Термостабилизация фиксацией тока базы. Схема каскада представлена на рисунке 2.18. 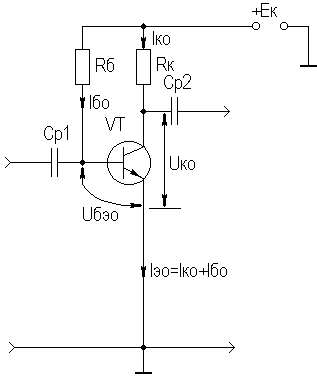 Рисунок 2.18. Каскад с фиксацией тока базы Rб определяется соотношением: 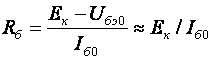 т.к. Eк>>Uбэ0. Очевидно, что Iб0 "фиксируется" выбором Rб, при этом ослабляется влияние первого фактора нестабильности тока коллектора (за счет смещения проходных характеристик). Коэффициенты термостабилизации для этой схемы таковы: 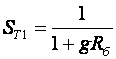 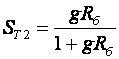 Отсюда видно, что данная схема имеет малую эффективность термостабилизации (ST2≈1). Коллекторная термостабилизация. Схема каскада представлена на рисунке 2.19а. 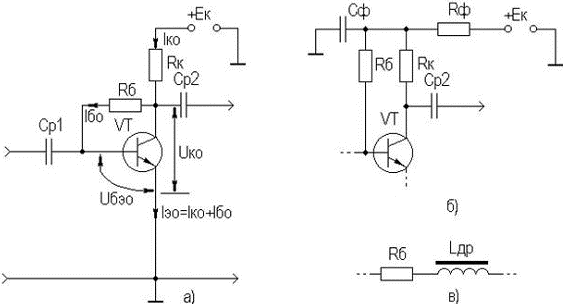 Рисунок 2.19. Каскад с коллекторной термостабилизацией (а) и его варианты (б, в) Rб определяется соотношением: 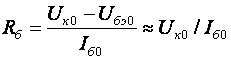 т.к. Uк0>>Uб0. Термостабилизация в этой схеме осуществляется за счет отрицательной обратной связи (ООС), введенной в каскад путем включения Rб между базой и коллектором БТ. Механизм действия ООС можно пояснить следующей диаграммой: T⇑⇒I⇑к0⇒U⇓к0⇒I⇓б0⇒I⇓к0, ↑←←←←петля ООС ←←←←↓ где символами ⇑ и ⇓ показано, соответственно, увеличение и уменьшение соответствующего параметра. Коэффициенты термостабилизации для этой схемы: 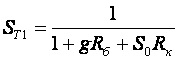 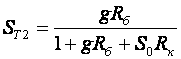 Из этих формул видно, что данная схема имеет лучшую термостабильность (ST1 и ST2 меньше единицы), чем схема с фиксированным током базы. В схеме коллекторной термостабилизации ООС влияет и на другие характеристики каскада, что должно быть учтено. Механизм влияния данной ООС на характеристики каскада будет рассмотрен далее. Схемные решения, позволяющие устранить ООС на частотах сигнала, приведены на рисунках 2.19б,в. В большинстве случаев, наилучшими свойствами среди простейших (базовых) схем термостабилизации обладает эмиттерная схема термостабилизации показанная на рисунке 2.20. 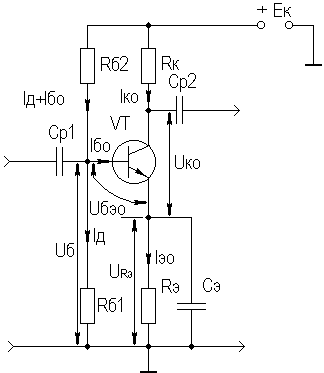 Рисунок 2.20. Каскад с эмиттерной термостабилизацией Эффект термостабилизации в этой схеме достигается: ◆ фиксацией потенциала Uб выбором тока базового делителя Iд>>Iб0, Uб≈const. ◆ введением по постоянному току ООС путем включения резистора Rэ. На частотах сигнала эта ООС устраняется шунтированием резистора Rэ емкостью Cэ. Напряжение Uбэ0 определяется как: Uбэ0 = Uб – URэ. Механизм действия ООС можно изобразить следующей диаграммой: T⇑⇒I⇑к0⇒U⇓Rэ⇒U⇓бэ0⇒I⇓б0⇒I⇓к0, ↑←←←←петля ООС ←←←←↓ где символами ⇑ и ⇓ показано, соответственно, увеличение и уменьшение соответствующего параметра. Эскизный расчет эмиттерной схемы термостабилизации маломощного каскада можно проводить в следующей последовательности: ◆ Зададимся током делителя, образованного резисторами Rб1 и Rб2: Iд = (3…10)Iб0; ◆ выбираем URэ = (0,1…0,2)Eк ≈ (1…5) В, и определяем номинал Rэ: 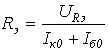 ◆ определяем потенциал Uб: Uб = URэ + Uбэ0; ◆ рассчитываем номиналы резисторов базового делителя: Rб1 = Uб/Iд, 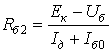 где Eк=Uк0+URэ+Iк0Rк, Rк определяется при расчете сигнальных параметров каскада. Коэффициенты термостабилизации для этой схемы: ST1 ≈ 1/(1 + S0·Rэ), 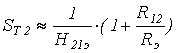 Здесь R12 — параллельное соединение резисторов Rб1 и Rб1. Для каскадов повышенной мощности следует учитывать требования экономичности при выборе Iд и URэ. Анализ полученных выражений показывает, что для улучшения термостабильности каскада следует увеличивать номинал Rэ и уменьшать R12. Для целей термостабилизации каскада иногда используют термокомпенсацию. Принципиальная схема каскада с термокомпенсацией приведена на рисунке 2.21. 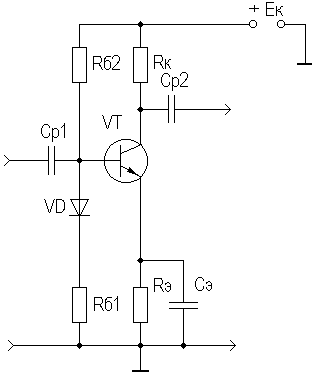 Рисунок 2.21. Каскад с термокомпенсацией Здесь в цепь базы транзистора включен прямосмещенный диод D, температурный коэффициент стабилизации напряжения (ТКН) которого равен ТКН эмиттерного перехода БТ. При изменении температуры окружающей среды напряжение Uбэ0 и напряжение на диоде Δφ0 будет меняться одинаково, в результате чего ток покоя базы Iб0 останется постоянным. Применение этого метода особенно эффективно в каскадах на кремниевых транзисторах, где основную нестабильность тока коллектора порождает ΔUбТ (из-за относительной малости ΔIкбо). Наилучшая реализация этого метода термокомпенсации достигается в ИМС, где оба перехода естественным образом локализуются в пределах одного кристалла и имеют совершенно одинаковые параметры. Возможно применение других термокомпенсирующих элементов и цепей, например, использующих сочетания БТ и ПТ. Большой класс цепей, питающих БТ, составляют схемы с двумя источниками питания, пример одной из них приведен на рисунке 2.22. 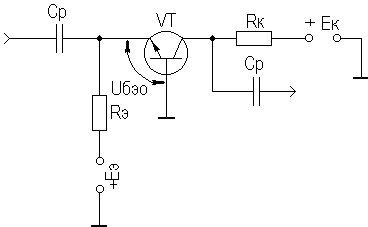 Рисунок 2.22. Каскад с двуполярным питанием По сути, это схема эмиттерной термостабилизации, у которой "жестко" зафиксирован потенциал Uб, Следует отметить возможность применения данных схем термостабилизации при любой схеме использования БТ в любой комбинации. 2.7. Усилительный каскад на биполярном транзисторе с ОБВариант схемы каскада с ОБ с эмиттерной схемой термостабилизации приведен на рисунке 2.23, схема каскада для частот сигнала — на рисунке 2.24. 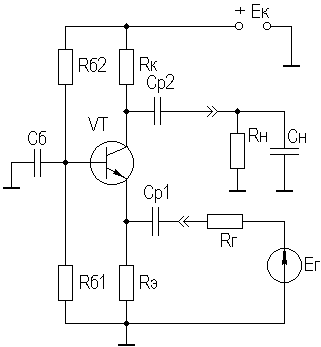 Рисунок 2.23. Усилительный каскад с ОБ 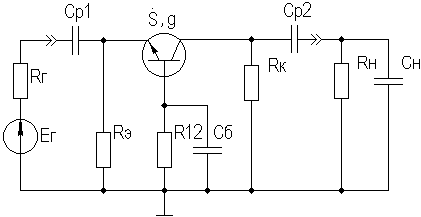 Рисунок 2.24. Схема каскада с ОБ для частот сигнала Каскад с ОБ называют еще "повторителем тока", т.к. коэффициент передачи по току этого каскада меньше единицы: KI = Iвых/Iвх = Iк/Iэ = H21э/(1 + H21э) = H21б. При подаче на эмиттер положительной полуволны синусоидального входного сигнала будет уменьшаться ток эмиттера, а, следовательно, и ток коллектора. В результате падение напряжение на Rк уменьшится, а напряжение на коллекторе увеличится, т.е. произойдет формирование положительной полуволны выходного синусоидального напряжения. Таким образом, каскад с ОБ не инвертирует входной сигнал. Анализ работы усилительного каскада с ОБ по входным и выходным динамическим характеристикам можно провести аналогично разделу 2.5. Для расчета параметров каскада с ОБ по переменному току используем методику раздела 2.3, а БТ представлять моделью предложенной в разделе 2.4.1. Представим каскад с ОБ схемами для областей СЧ, ВЧ и НЧ (рисунок 2.25 а,б,в): 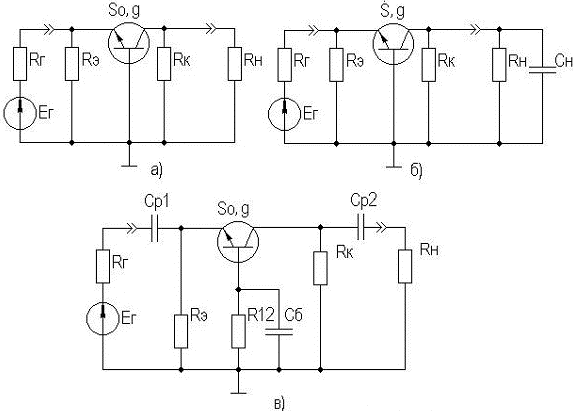 Рисунок 2.25. Схемы каскада с ОБ для СЧ, ВЧ и НЧ Проведя анализ, получим для области СЧ: K0 = S0Rэкв, где Rэкв ≈ Rк ∥ Rн; gвх = (S0 + g) + Gэ ≈ S0, где Gэ = 1/Rэ, обычно S0 >> g и Gэ. gвых ≈ g = 1/Rк. Эти соотношения получены в предположении, что низкочастотное значение внутренней проводимости транзистора g22э много меньше gк и gн. Это условие (если не будет оговорено особо) будет действовать и при дальнейшем анализе усилительных каскадов на БТ. Такое допущение справедливо потому, что БТ является токовым прибором и особенно эффективен при работе на низкоомную нагрузку. В области ВЧ получим:
где τв — постоянная времени каскада в области ВЧ, определяемая аналогично ОЭ.
где Cвых — выходная емкость каскада, Cвых=CкS0rб. 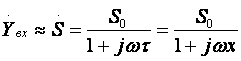 т.е. модуль входной проводимости уменьшается с ростом частоты, что позволяет сделать вывод об индуктивном характере входной проводимости каскада с ОБ на ВЧ. Количественно индуктивную составляющую входного импеданса можно оценить следующим образом: LвхОБ = rб/2πfTm где m = (1,2…1,6). Выражения для относительного коэффициента передачи Yв и коэффициента частотных искажений Mв и соотношения для построения АЧХ и ФЧХ каскада с ОБ аналогичны приведенным в разделе 2.5 для каскада с ОЭ. В области НЧ получим: Kн = K0/(1 + 1/jωτн), где τн — постоянная времени разделительной цепи в области НЧ. Далее все так же, как для каскада с ОЭ, за исключением расчета базовой блокировочной цепи, постоянная времени которой приближенно оценивается следующей формулой: τнб ≈ Cб/g, сопротивление БТ со стороны базы приблизительно равно 1/g, а влиянием R12 можно пренебречь, обычно R12 >> 1/g. 2.8. Усилительный каскад на биполярном транзисторе с ОКСхема каскада с ОК с эмиттерной схемой термостабилизацией приведена на рисунке 2.26. 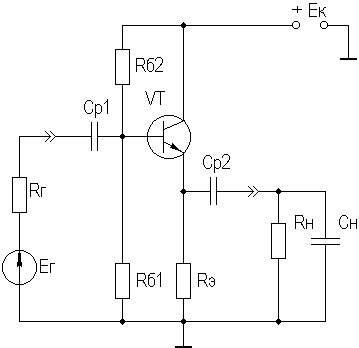 Рисунок 2.26. Усилительный каскад с ОК Схема для частот сигнала изображена на рисунке 2.27. 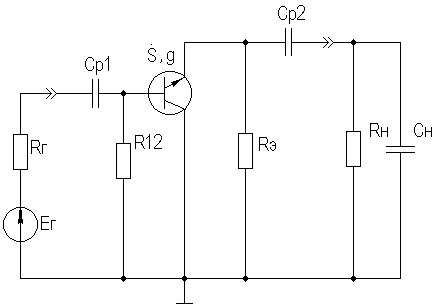 Рисунок 2.27. Схема каскада с ОК для частот сигнаа Каскад с ОК называют еще "повторителем напряжения" или "эмиттерным повторителем", т.к. коэффициент передачи по напряжению этого каскада меньше единицы, что вытекает из его дальнейшего анализа. При подаче на базу положительной полуволны входного синусоидального сигнала будет увеличиваться ток коллектора и, следовательно, ток эмиттера. В результате падение напряжения на Rэ увеличится, т.е. произойдет формирование положительной полуволны выходного напряжения. Таким образом, каскад с ОК не инвертирует входной сигнал. Напряжение сигнала, приложенное к эмиттерному переходу, является разностью между Uвх и Uвых. Чем больше и Uвых (при заданном Uвх), тем меньше окажется напряжение, приложенное к эмиттерному переходу, что будет приводить к уменьшению тока эмиттера и, соответственно, к уменьшению Uвых, т.е. в каскаде с ОК проявляется действие ООС, причем 100%-ной. Анализ работы усилительного каскада с ОК по входным и выходным динамическим характеристикам проводится как для ОЭ (см. раздел 2.5). Для расчета параметров каскада с ОК по переменному току используем методику раздела 2.3, а БТ представлять моделью предложенной в разделе 2.4.1. Представим каскад с ОК схемами для областей СЧ, ВЧ и НЧ (рисунок 2.28 а,б,в):  Рисунок 2.29. Схемы каскада с ОК для СЧ, ВЧ и НЧ Проведя анализ, получим для области СЧ: 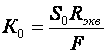 где Rэкв = Rэ ∥ Rн, F = 1 + S0Rэкв — глубина ООС; Rвх = R12 ∥ Rвх T, где Rвх T — входное сопротивление собственно транзистора, Rвх T = rб + (1 + H21э)·(rэ + Δr + Rэкв); Rвых = R12 ∥ Rвых T, где Rвых T — выходное сопротивление собственно транзистора, 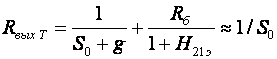 т.к. S0>>g и при работе каскада от низкоомного источника сигнала (при этом Rб=R12∥Rг) второе слагаемое оказывается существенно меньше первого. В целом Rвых ≈ 1/S0, потому, что, как правило, Rэ >> 1/S0. В области ВЧ получим: 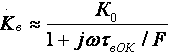 где τвОК — постоянная времени каскада в области ВЧ, τвОК =(τ+CнRэкв)/F; τ — постоянная времени БТ. Yвх ≈ 1/R12 + (1/RвхT + jωCвх дин), где Cвх дин=Cк+Cн/(H21э+1), т.е. каскад с ОК имеет входную динамическую емкость меньшую, чем каскад с ОЭ; 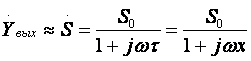 т.е. модуль выходной проводимости уменьшается с ростом частоты, что позволяет сделать вывод об индуктивном характере выходной проводимости каскада с ОК на ВЧ. Количественно индуктивную составляющую выходного импеданса можно оценить следующим образом: LвыхОК = rб/2πfTm где m=(1,2…1,6). Выражения для относительного коэффициента передачи Yв и коэффициента частотных искажений Mв и соотношения для построения АЧХ и ФЧХ каскада с ОК аналогичны приведенным в разделе 2.5 для каскада с ОЭ. В области НЧ получим: Kн = K0/(1 + 1/jωτн), где τн — постоянная времени разделительной цепи в области НЧ. далее все так же, как для каскада с ОЭ. Характеристики БТ при различных схемах включения приведены в таблице 2.1. Таблица 2.1 Характеристики БТ при различных схемах включения
2.9. Усилительный каскад на полевом транзисторе с ОИСреди усилительных каскадов, выполненных на полевых транзисторах, наиболее широкое применение получил каскад, в котором ПТ включен по схеме с общим истоком. На рисунке 2.29 приведена принципиальная схема наиболее распространенного варианта каскада с ОИ с цепью автосмещения, служащей для обеспечения режима работы ПТ по постоянному току. Если БТ разделяется на два типа — p-n-p и n-p-n, отличающиеся противоположными полярностями питающих напряжений, то разновидностей ПТ существует, по меньшей мере, шесть. Рассмотрим схему рисунка 2.29, где изображен ПТ с p-n переходом и n-каналом. Анализ каскадов на других типах ПТ будет отличаться лишь в незначительных деталях. 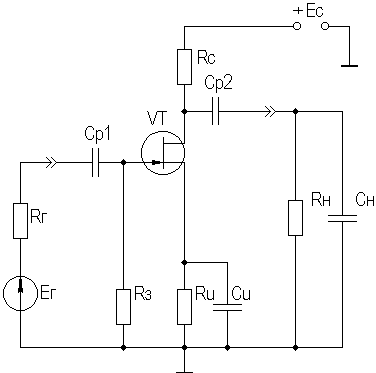 Рисунок 2.29. Усилительный каскад с ОИ Выходные статические вольтамперные характеристики (ВАХ) ПТ представлены на рисунке 2.30. В отличие от БТ, у ВАХ ПТ имеется значительная область управляемого сопротивления, в которой возможно использование ПТ в качестве электронного управляемого резистора. В качестве усилительного элемента ПТ используется в области усиления. 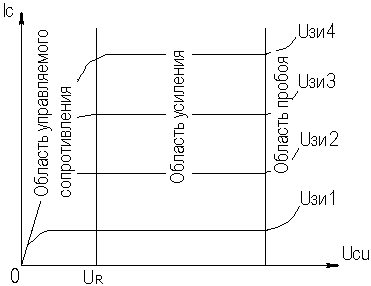 Рисунок 2.30. Выходные статические характеристики ПТ В отсутствие входного сигнала каскад работает в режиме покоя. С помощью резистора Rи задается напряжение смещения U0=Iс0·Rи, которое определяет ток покоя стока Iс0. Координаты рабочей точки определяются соотношениями: Uс0 ≥ Uвых + UR, где UR — граница области управляемого сопротивления на выходных статических характеристиках транзистора (рисунок 2.30), UR ≈ (1…2) В; Iс0 ≥ Uвых/R≈, где R≈= Rс∥Rн — сопротивление нагрузки каскада по переменному току;
где Uотс — напряжение отсечки, Iси — ток стока при Uзи=0 В (либо при Uзи=2Uотс для ПТ в режиме обогащения, см. рисунок 2.33 в подразделе 2.10). С помощью резистора Rи, помимо задания необходимого напряжения смещения, в каскад вводится ООС, способствующая термостабилизации (у ПТ как и у БТ наблюдается сильная температурная зависимость параметров), на частотах сигнала эта ОС устраняется путем включения Cи. Графически проиллюстрировать работу каскада с ОИ можно, используя проходные и выходные статические характеристики ПТ, путем построения его динамических характеристик. Построение во многом аналогично каскаду с ОЭ и отдельно не рассматривается. Нетрудно показать, что каскад с ОИ, как и каскад с ОЭ, инвертирует входной сигнал. На рисунке 2.31 а,б,в приведены, соответственно, малосигнальные схемы для областей СЧ,НЧ, и ВЧ. 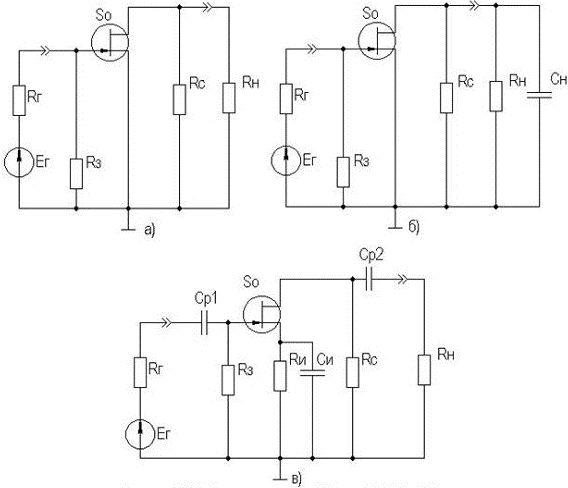 Рисунок 2.31. Схемы каскада с ОИ для СЧ, ВЧ и НЧ Для расчета параметров усилительного каскада по переменному току удобно использовать методику, описанную в разделе 2.3, а ПТ представить моделью, предложенной в разделе 2.4.2. В результате расчета в области СЧ получим: K0 = S0Rэкв, где Rэкв= Rс∥Rн; gвх ≈ 1/Rз, gвых ≈ gс = 1/Rз. Эти соотношения получены в предположении, что низкочастотное значение внутренней проводимости транзистора g22э много меньше gс и gн. Это условие (если не будет оговорено особо) будет действовать и при дальнейшем анализе усилительных каскадов на ПТ. В области ВЧ получим:
где τв — постоянная времени каскада в области ВЧ, τв≈CнRэкв; 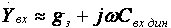 где Cвхдин = Cзи + Cзс(1 + K0); 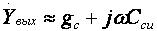 Выражения для относительного коэффициента передачи Yв и коэффициента частотных искажений Mв и соотношения для построения АЧХ и ФЧХ каскада с ОК аналогичны приведенным в разделе 2.5 для каскада с ОЭ. В области НЧ получим: Kн = K0/(1 + 1/jωτн), где τн — постоянная времени разделительной цепи в области НЧ. далее все так же, как для каскада с ОЭ. 2.10. Термостабилизация режима каскада на ПТРазличают, по крайней мере, шесть типов ПТ, показанные на рисунке 2.32. 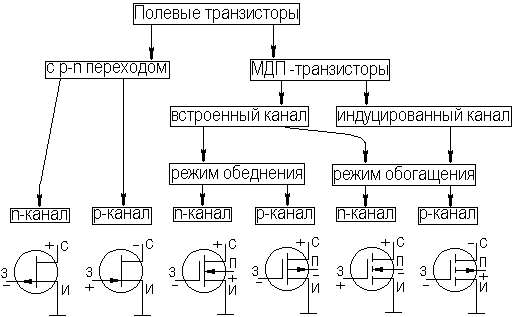 Рисунок 2.32. Основные типы ПТ Проходные характеристики n-канальных ПТ в режиме обогащения, смешанном и обеднения приведены, соответственно на рисунке 2.33 а,б,в, для p-канальных ПТ они будут отличаться противоположной полярностью питающих напряжений. 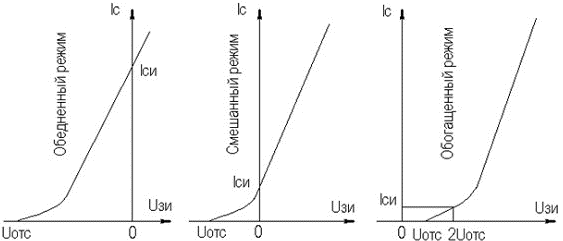 Рисунок 2.33. Проходные характеристики ПТ С помощью рассмотренной схемы автосмещения (рисунок 2.29) возможно обеспечение требуемого режима по постоянному току для ПТ, имеющих проходную характеристику, изображенную на рисунке 2.33а, и — (при отрицательном смещении) — на рисунке 2.33б. Более универсальной схемой питания ПТ является схема с делителем в цепи затвора (рисунок 2.34), способная обеспечить любую полярность напряжения смещения Uзи0. 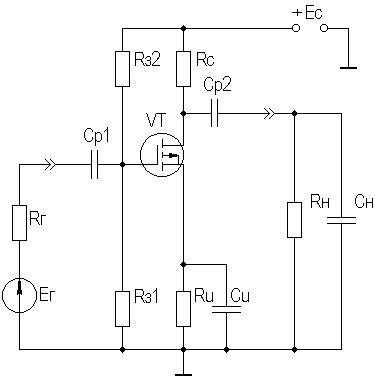 Рисунок 2.34. Схема питания ПТ с делителем в цепи затвора В [1] приведен ряд полезных практических соотношений: 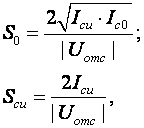 где соответствующие токи показаны на рисунке 2.33, а Sси — крутизна при токе стока равном Iси. В ПТ температурная нестабильность тока стока обусловлена следующими факторами (при росте температуры): ◆ увеличением тока стока за счет теплового смещения проходных характеристик (как и в БТ) при малых значениях тока покоя стока Iс0; ◆ уменьшением тока стока за счет удельного сопротивления канала в широком диапазоне изменения тока покоя стока Iс0. Следовательно, у некоторых типов ПТ возможно существование термостабильной точки покоя (рисунок 2.35). 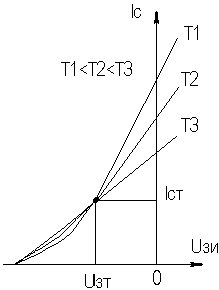 Рисунок 2.35. Температурная зависимость тока стока Координаты термостабильной точки и соответствующую им крутизну можно приближенно оценить по следующим соотношениям [1]: UзT ≈ Uотс – 0,63 В; IсT = 0,4·Iси/U²отс ≈ (0,1…0,6) мА; S0T ≈ IсT/0,32. Поскольку ток IсT относительно мал, можно сделать вывод, что широком диапазоне изменений тока стока последний уменьшается с ростом температуры. Рассмотренные основные схемы питания ПТ осуществляют термостабилизацию режима за счет ООС (последовательной по постоянному току) аналогично каскаду на БТ, т.е. уход тока стока уменьшается в (1 + S0Rи) раз. Собственно ΔIс0 определяется по справочным данным, составляющую теплового смещения проходных характеристик можно определить по аналогии с БТ. Отрицательная температурная зависимость тока стока ПТ может быть использована в целях термокомпенсации каскадов на БТ. 2.11. Усилительный каскад на полевом транзисторе с ОСВариант схемы каскада с ОС с автосмещением приведен на рисунке 2.36, схемы для областей СЧ,ВЧ и НЧ приведены, соответственно, на рисунках 2.37а,б,в. 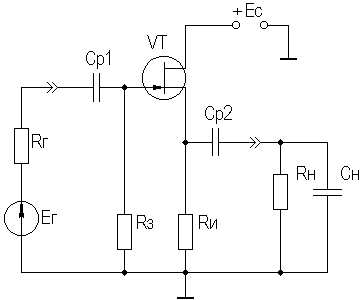 Рисунок 2.36. Усилительный каскад с ОС 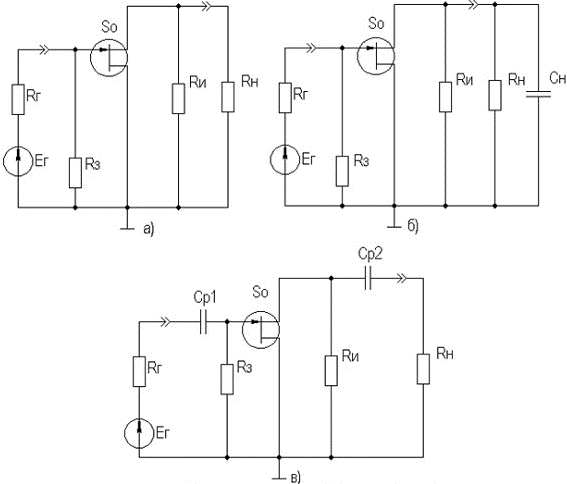 Рисунок 2.37. Схемы каскада с ОС для СЧ, ВЧ и НЧ Каскад с ОС называют еще "истоковым повторителем" или "повторителем напряжения, т.к., аналогично каскаду с ОК, можно показать, что коэффициент передачи по напряжению этого каскада меньше единицы, и что каскад с ОС не инвертирует фазу входного сигнала. Графический анализ работы усилительного каскада с ОС проводится как для ОЭ (см. раздел 2.5). Для расчета параметров каскада с ОС по переменному току используем методику раздела 2.3, а ПТ представлять моделью предложенной в разделе 2.4.2. Проведя анализ, получим для области СЧ:
где Rэкв= Rи∥Rн, F = 1 + S0Rэкв — глубина ООС; Rвх ≈ Rз, Rвых = Rи ∥ Rвых T, где Rвых T — выходное сопротивление собственно транзистора, Rвых T ≈ 1/S0. В целом Rвых T ≈ 1/S0, потому, что, как правило, Rи >> 1/S0. В области ВЧ получим: 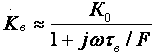 где τв — постоянная времени каскада в области ВЧ, определяемая аналогично ОИ; Yвх ≈ 1/Rз + jωCвх дин, где Cвх дин = Cзи + Cн·(K0 + 1); 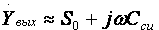 Выражения для относительного коэффициента передачи Yв и коэффициента частотных искажений Mв и соотношения для построения АЧХ и ФЧХ каскада с ОК аналогичны приведенным в разделе 2.5 для каскада с ОЭ. В области НЧ получим: Kн = K0/(1 + 1/jωτн), где τн — постоянная времени разделительной цепи в области НЧ. далее все так же, как для каскада с ОИ. Усилительный каскад с ОЗ (рисунок 2.38) на практике используется редко, поэтому отдельно рассматриваться не будет. Отметим только, входное сопротивление каскада определяется аналогично выходному для истокового повторителя (≈1/S0), а остальные параметры — аналогично ОИ. 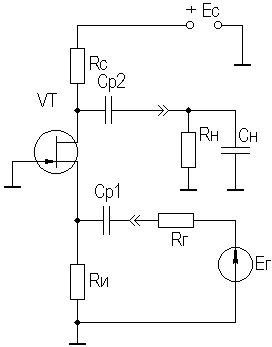 Рисунок 2.38. Усилительный каскад с ОЭ Характеристики ПТ при различных схемах включения приведены в таблице 2.2. Таблица 2.2 Характеристики ПТ при различных схемах включения
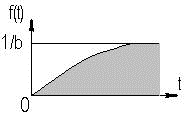
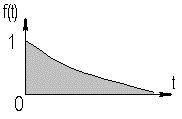
2.12. Временные характеристики усилительных каскадов2.12.1. Метод анализа импульсных искаженийРассмотренные усилительные каскады могут быть использованы для усиления импульсных сигналов. Для оценки искажений формы усиливаемых импульсных сигналов необходимо рассмотреть переходные процессы в усилительных каскадах. При анализе переходных процессов будем считать каскады линейными, т.е. амплитуда сигналов в них существенно меньше постоянных составляющих токов и напряжений в рабочей точке. В этом случае наиболее удобным методом анализа является преобразование Лапласа (операторный метод). Временной процесс в электрической цепи описывается системой интегро-дифференциальных уравнений (СИДУ). Применяя прямое преобразование Лапласа (ППЛ), приводят СИДУ к системе линейных алгебраических уравнений (СЛАУ), которая просто решается относительно некоторой промежуточной функции, по которой с помощью обратного преобразования Лапласа (ОПЛ) находится решение для исходной СИДУ. ППЛ функции вещественного переменного f(t) ("оригинала") служит для нахождения преобразованной функции f(p) ("изображения") и определяется соотношением: 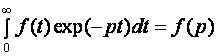 ОПЛ определяется формулой: 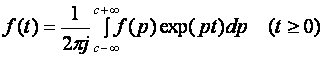 где p = α + jω. Практически "оригинал" f(t) находят по изображению f(p) с помощью таблиц [6], три примера приведены в таблице 2.3. Таблица 2.3 Обратное преобразование Лапласа
Из теоремы о предельных значениях следует, что если f(t)≡f(p), то: 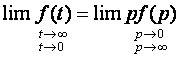 Применительно ПХ h(t) получим: 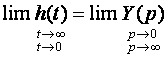 где Y(p) получается из АЧХ заменой jω на p, и учитывая, что "изображение" единичного скачка равно 1/p (см. таблицу 2.3). Из последнего выражения следует, что при временном анализе усилительного каскада возможно отдельное рассмотрение областей малых времен (МВ) и больших времен (БВ) по схемам каскада для областей ВЧ и НЧ соответственно, и нахождения ty и Δ (см. рисунок 2.5). Итак, анализ усилительных каскадов при импульсных сигналах сводится к следующим операциям: ◆ зная Y(jω), заменой jω на p и делением на p полученного выражения переводят его в "изображение" ПХ h(p); ◆ пользуясь таблицей, по h(p) находят "оригинал" ПХ h(t); ◆ рассматривая h(t) для схемы каскада в ВЧ области, находят ty, δ и их зависимость от элементов; ◆ рассматривая h(t) для схемы каскада в НЧ области, находят Δ и его зависимость от элементов; ◆ исходя из допустимых искажений импульсного сигнала, получают формулы для выбора элементов схемы каскада. Из-за сильного изменения параметров транзистора от тока при больших амплитудах импульсного сигнала (одного порядка с амплитудами напряжения и тока в рабочей точке) и использовании упрощенных моделей ПТ и БТ (до 0,5fT), что не позволяет вести учет высших гармонических составляющих спектра сигнала, вносящих существенный вклад в искажения формы сигнала, эскизный расчет усилительных каскадов во временной области характеризуется большей (в сравнении с расчетом в частотной области) погрешностью. В какой-то степени скорректировать погрешность можно путем учета времени запаздывания tз (см. рис.2.4), и усреднением параметров транзистора за время действия импульсного сигнала (рисунок 2.39). 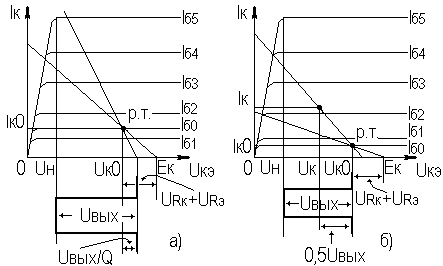 Рисунок 2.39. Выходные ДХ каскада с ОЭ – импульсного усилителя В отличие от усилительных каскадов гармонических сигналов, при выборе транзисторов для импульсных каскадов следует учитывать полярность выходного сигнала при выборе типа проводимости транзистора с целью экономии энергии источника питания. Если ИУ предназначен для усиления однополярного сигнала, то с энергетических соображений рекомендуется брать транзистор проводимости p-n-p для выходного сигнала положительной полярности n-p-n — для отрицательной. На рисунке 2.39а проиллюстрирован процесс выбора рабочей точки для импульсных сигналов с малой скважностью (Q≤10). Скважность Q определяется как отношение длительности периода следования импульсов к их длительности. Определить координаты рабочей точки (и точки, для которой рассчитываются параметры транзистора) можно, используя следующие соотношения: 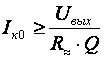 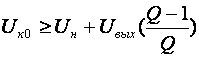 На рисунке 2.39б проиллюстрирован процесс выбора рабочей точки для импульсных сигналов с большой скважностью (Q>10). Определить координаты рабочей точки можно, используя следующие соотношения: Uк0 ≥ Uн + Uвых. Выбор Iк0 ограничен снизу нелинейной областью характеристик транзистора и необходимым допуском на возможное его уменьшение при изменении температуры, обычно Iк0 ≈ (3…10) мА. Расчет усредненных параметров транзистора в этом случае следует вести для точки с координатами: Uк ≥ Uн + 0,5·Uвых; 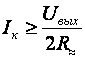 Для импульсных сигналов типа "меандр" (Q=2) выбор рабочей точки и типа проводимости транзистора аналогичен случаю гармонического сигнала. Хотя приведенные выше соотношения ориентированы на БТ, на них следует ориентироваться и при расчете каскадов на ПТ, учитывая особенности последних. 2.12.2. Анализ усилительных каскадов в области малых временВыражение для относительного коэффициента передачи усилительных каскадов на БТ и ПТ в области ВЧ имеет вид: Yв(jω) = 1/(1 +jωτв). Получим выражение для переходной характеристики: hв(p) = Yв(p)/p = 1/p(1 + pτв). По таблице 2.3 получим "оригинал": hв(t) = 1 – exp(-t/τв). Воспользовавшись определением времени установления (см. рисунок 2.4), получим: hв(t1) = –exp(-t1/τв) = 0,1; отсюда exp(-t1/τв) = 0,9; hв(t2) = –exp(-t2/τв) = 0,9; отсюда exp(-t2/τв) = 0,1; тогда exp[(t2-t1)/τв] = exp(ty/τв]) = 0,9; и окончательно получаем: ty = 2,2τв. Из анализа выражения для hв(t) следует, что процесс установления амплитуды заканчивается через t=(3…4)τв, следовательно, чтобы не было уменьшения K0 каскада из-за не достижения установившегося режима, необходимо, чтобы длительность импульса была: Tи ≥ (3…4)τв. Учесть время запаздывания tз для каскада на БТ можно следующим образом: 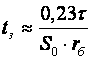 2.12.3. Анализ усилительных каскадов в области больших временВыражение для относительного коэффициента передачи усилительных каскадов на БТ и ПТ в области НЧ имеет вид: Yн(jω) = jωн/(1 + jωτн). Получим выражение для переходной характеристики: hн(p) = Yн(p)/p = τн/(1 + pτн). 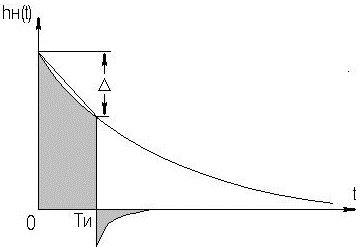 Рисунок 2.40. Переходный процесс в области БВ По таблице 2.3 получим "оригинал": hн(t) = –exp(–t/τн). При Tи≤τн, разлагая hн(t) в степенной ряд и ограничившись двумя членами, при t=Tи (рисунок 2.40) получаем для случая малых искажений плоской вершины импульса (Δ≤20%): hн(t) = –exp(–t/τн) ≈ 1 – Tи/τн = 1 – Δ, откуда: Δ = Tи/τн. 2.12.4. Связь временных и частотных характеристик усилительных каскадовТ.к. временные и частотные характеристики каскадов выражаются через постоянные времени τв и τн, то легко получить связывающие их выражения. Итак: fв = 1/2πτв, fн = 1/2πτн, tу = 2,2·τв, Δ = Tи/τн. откуда при Mв = Mн = 3 дБ получаем: fв = 2,2/2πτв = 0 ,35tу, fн = Δ/2πτнTи. 2.13. Простейшие схемы коррекции АЧХ и ПХЦелью коррекции является расширение диапазона рабочих частот, как в области ВЧ, так и в области НЧ в усилителях гармонических сигналов, либо уменьшение искажений в областях МВ и БВ в усилителях импульсных сигналов. В области ВЧ (МВ) применяется простая параллельная индуктивная коррекция. Более сложные варианты индуктивной коррекции применяются редко из-за сложности настройки и трудности при реализации УУ в микроисполнении. Схема каскада с простой параллельной индуктивной ВЧ-коррекцией на ПТ со схемой для области ВЧ (МВ) приведены на рисунке 2.41. 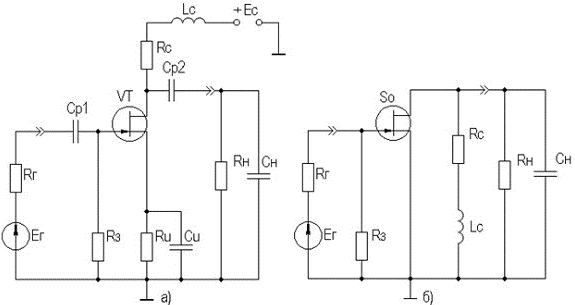 Рисунок 2.41. Каскад на ПТ с простой параллельной коррекцией Физически эффект увеличения fв объясняется относительным увеличением коэффициента передачи на ВЧ за счет увеличения эквивалентной нагрузки каскада (путем добавления индуктивного сопротивления ZLс в цепь стока). Эффект уменьшения tу объясняется увеличением тока через емкость Cн (что сокращает время ее заряда и, следовательно, уменьшает tу) за счет того, что в начальный момент выходной ток транзистора практически весь направляется в цепь RнCн, его ответвлению в стоковую цепь препятствует ЭДС самоиндукции в индуктивности Lс. В [6] приводятся основные выражения для расчета каскадов с простой индуктивной параллельной ВЧ коррекцией для случая, когда Rн>>Rс, что практически всегда имеет место в промежуточных каскадах на ПТ: 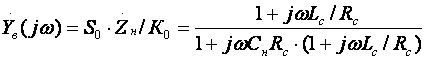 После преобразования получаем: 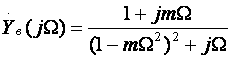 где Ω — нормированная частота, Ω = ωτв, τв = RсCн; m — коэффициент коррекции, по физическому смыслу представляющий собой квадрат добротности (Qк) параллельного колебательного контура LсRсCнRн (см. рисунок 2.41б), m≈Lс/(CнRн²)=Qк². Модуль полученного выражения дает АЧХ корректированного каскада: 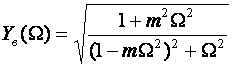 Максимально плоская АЧХ получается, когда m=0,414 [6]. Данное условие вытекает из равенства нулю производной Yв(Ω) при Ω=0, т.е. АЧХ не должна иметь наклона в точке W=0. ФЧХ корректированного каскада определяется выражением: φв = arctg[(m – 1)Ω – m²Ω³]. ФЧХ максимально линейна, если m=0,322 [6]. Добротность Qк=0,5 соответствует границе между апериодическими и колебательными разрядами конденсатора контура LсRсCнRн, поэтому при m≤0,25 выброса в ПХ не будет, т.к. не будет затухающих колебаний в контуре. На рисунке 2.42 приведены нормированные АЧХ и ПХ каскадов на ПТ с простой параллельной индуктивной коррекцией для различных коэффициентов коррекции m. 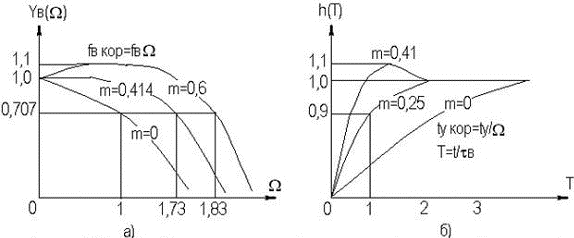 Рисунок 2.42. АЧХ и ПХ каскадов с простой параллельной индуктивной коррекцией Для оценки эффективности УУ вводят понятие площади усиления П для ШУ и импульсной добротности D для ИУ: Π = K0·fв, D = K0/tу, Π = 0,35·D. Как видно из рисунка 2.42, максимальный выигрыш по этим параметрам в каскаде на ПТ для рассмотренного варианта коррекции и отсутствии подъема АЧХ на ВЧ (выброса ПХ в области МВ), составляет 1,73 [6] раза. Следует подчеркнуть, что данный выигрыш получается при условии когда Rн>>Rс, что обычно имеет место при использовании каскада на ПТ в качестве промежуточного в УУ. В каскадах на БТ (схема не приводится ввиду ее подобия рисунку 2.41) анализ эффективности простой параллельной индуктивной коррекции сложнее из-за необходимости учета частотной зависимости крутизны БТ, Выражение для относительного коэффициента передачи имеет вид [6]: 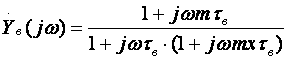 здесь τв=τ+τ1+τ2 — постоянная времени каскада без коррекции на ВЧ; m=Lс(Rк·τв) — коэффициент коррекции; х=(τ+τ1)/τв — отношение составляющих постоянной времени каскада. Данное выражение не позволяет однозначно оценить выигрыш, даваемый простой параллельной индуктивной коррекцией в каскадах на БТ, поэтому либо приходится прибегать к помощи ЭВМ, либо пользоваться таблицами, приведенными, например, в [6]. Анализ показывает, что выигрыш в площади усиления (импульсной добротности) может достигать величины, равной 0,5S0rб, т.е. величины, большей двух раз (теоретически до 20, практически 2…10). Анализ так же показывает, что простая параллельная индуктивная коррекция в каскаде на БТ наиболее эффективна при малых х, что соответствует случаю применения относительно низкочастотных транзисторов. В целом же следует заметить, что, несмотря на некоторую эффективность, простая параллельная индуктивная коррекция в современной схемотехнике УУ используется редко. Это объясняется, в первую очередь, технологическими трудностям реализации индуктивностей в ИМС, и сильной зависимостью эффекта коррекции от параметров транзистора, что требует подстройки схемы в случае их разброса. Возможно использование вместо катушки индуктивности индуктивного входного сопротивления каскада с ОБ (рисунок 2.43). 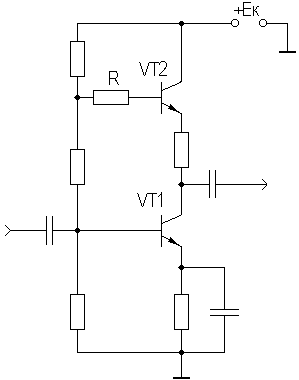 Рисунок 2.43. Коррекция входным сопротивлением каскада с ОБ Индуктивность транзистора VT2 между эмиттером и общим проводом равна: L = (rб + R)/2πfTk, где k=(1,2…1,6). Резистор R служит для увеличения индуктивности и ее подстройки (при гибридно-пленочной технологии лазерной подгонкой или выносными резисторами). В области НЧ (БВ) находит применение коррекция коллекторным (стоковым) фильтром. Схема каскада с НЧ-коррекцией на БТ и его упрощенная (учитывающая влияние только Cp2) схема для области НЧ изображены на рисунке 2.44. Физически уменьшение fн объясняется относительным увеличением коэффициента передачи в области НЧ за счет увеличения эквивалентной нагрузки каскада путем добавления емкостного сопротивления ZCф в цепь коллектора на НЧ. Эффект уменьшения спада плоской вершины импульса Δ поясняется эпюрами напряжения, приведенными на рисунке 2.44б. 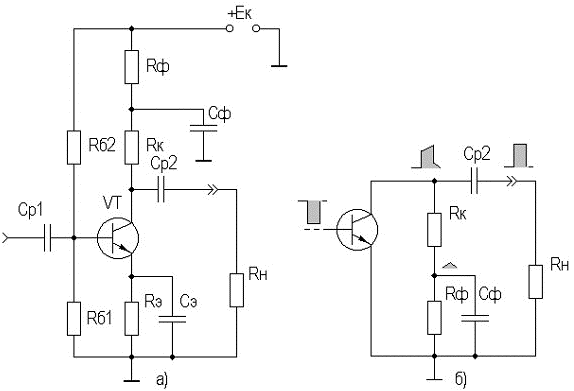 Рисунок 2.44. Каскад на БТ с НЧ-коррекцией В идеальном случае, при Rф=∞, условием коррекции будет равенство постоянных времен RкCф и RнCp2 [6]. В реальных схемах рекомендуется брать Rф=(1…2)Rк, для подъема вершины импульса на (10…20)% можно воспользоваться соотношением: Δ↑ ≈ Tи/(RнCф). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Главная | В избранное | Наш E-MAIL | Прислать материал | Нашёл ошибку | Наверх |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

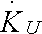 или просто
или просто 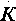 :
: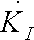 :
: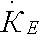 :
: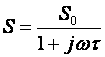 ),
),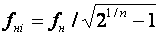 .
.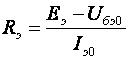 , а ST12≈1/H21э.
, а ST12≈1/H21э.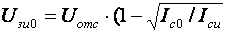 ),
),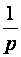
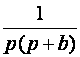
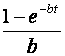
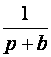
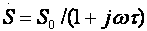 .
.