Жизнь шла своим чередом, и тайны пространства, которые в первое время привлекали всеобщее внимание, все больше отступали на задний план. Обыватель, не особенно разбиравшийся в этих проблемах, давно уже говорил о другом и лишь иногда недоуменно задавал себе вопрос: «И зачем только ученые выдумывают всякие непонятные вещи?» Сами ученые, а к их числу я отношу и математиков, и естествоиспытателей, теперь все были убеждены в возможности существования миров с числом измерений, превышающим 2, хотя большинство сомневалось, что такие миры реально существуют. К разговорам о визитах из трехмерного пространства к нам, в Двухмерие, так называемой Сферы, или Гиперокружности, такие ученые относились как к выдумке, но ценили подобные фантазии, ибо те позволяли им знакомить широкую публику с геометрическими свойствами иных мыслимых миров. Однако вскоре произошли события, которые заставили всех совершенно по-новому взглянуть на всю совокупность проблем, связанных с пространством.

Однажды (я хорошо помню этот вечер) мы сидели по своему обыкновению в семейном кругу, как вдруг кто-то из моих детей спросил, слышали ли мы новость: директора Тригонометрической службы освободили от занимаемой должности. Меня это сообщение удивило. Не имея чести быть лично знакомым с директором, я тем не менее знал его как пунктуального служащего, весьма сведущего в науке и технике, который пользовался к тому же широкой известностью как искусный и точный наблюдатель. Что явилось причиной его внезапного позорного изгнания?

Моя жена высказала предположение, что снятый с поста директор мог питать пристрастие к деньгам (такое иногда случается с самыми высокопоставленными чиновниками), по я не мог поверить, чтобы многоугольник, посвятивший себя науке и получавший огромное жалование, был способен пойти на преступление.

— Мало ли с какими финансовыми затруднениями мог столкнуться директор, — возразила мне жена. — Не исключено, что он потерял много денег на каких-нибудь спекуляциях.

— Может быть, у него расточительная жена, — высказал новое предположение мой сын.

— Или транжира сын, — в пику ему подхватила моя жена.

В то время мы еще ничего не знали об истинных причинах увольнения директора и могли лишь строить догадки.

— А что такое Тригонометрическая служба? — спросил мой старший внук.

— Служба, которая занимается измерением углов треугольников, — пояснил я.

— Я тоже знаю, как это делать, — ответил мой внук. — Ведь, в конце концов, каждый из нас с полным правом может называть себя угломером. У всех, кто встречается мне на улице, я прежде всего измеряю обращенный ко мне угол — прикидываю на глаз его величину. Такая оценка, как известно, оказывается очень точной— то ли от постоянных упражнений, то ли в силу врожденной способности измерять углы. В школе нас также, к сожалению, заставляют заниматься этим более чем скучным делом. А тому, кто умеет измерить утлы, известен и сам треугольник.

— И все же измерение углов необходимо, — возразил я. — Время, потраченное на изучение этого тонкого искусства, нельзя считать потерянным напрасно. Каждый, кто быстро оценивает величину углов, хорошо разбирается в людях!

— Я не спорю, — признал мою правоту внук. — Просто мне хотелось сказать, что в измерении углов нет ничего особенно сложного — оно доступно каждому. Если же нам требуется измерить углы более точно, то их можно ощупать или обратиться в специально созданные для этой цели учреждения, где любому желающему не только измерят с высокой точностью его угол, но и выдадут официальное удостоверение о результатах измерения. И мне никогда не приходилось слышать, чтобы подобными делами занималась Тригонометрическая служба.

— Замечание вполне справедливое, — согласился я. — Тригонометрическая служба учреждена специально для того, чтобы путем измерения треугольников составить точную карту мира. Для этого весь мир был разбит на треугольники (триангулирован, или покрыт триангуляционной сетью), их углы измерены, а длины сторон вычислены.

— Дедушка, — укоризненно воскликнул мой младший внук, — как ты можешь так говорить! Разве можно вычислить длины сторон треугольника, зная лишь его углы?

— Разумеется, нельзя, — успокоил я внука, — в этом ты совершенно прав. Необходимо еще знать длину какой-нибудь из сторон. Тогда, точно измерив углы треугольника, можно вычислить длины остальных сторон.

— Для вычисления всех сторон треугольника достаточно знать длину одной из сторон и величину двух углов. Третий угол вычислить совсем не трудно, поскольку сумма всех углов треугольника равна двум прямым углам, или 180°, — счел необходимым добавить маленький всезнайка.

Я был горд его замечанием. Оно еще раз свидетельствовало о том, что малыш шел но стопам своих предков. Разве не был основатель нашего рода, знаменитый Квадрат, его прапрадедом?

На некоторое время в комнате воцарилась тишина. Каждый размышлял над необычайным происшествием. Первой нарушила молчание моя жена. Она сказала:

— Не понимаю, каким образом в вычислении сторон треугольников директор Тригонометрической службы усмотрел повод для того, чтобы совершить мошенничество. Может быть, директор злоупотребил своим правом выбирать вершины триангуляционной сети? Впрочем, выбор вершин — задача чисто техническая.

— Неизвестно, сколь строго следил директор за тем, как выполняют свои обязанности сотрудники Тригонометрической службы, — вмешалась в разговор жена моего сына, — а здесь-то и могли совершаться различные мошеннические проделки.

— Не будем больше говорить на эту тему, — потребовал я. — Мы ничего достоверно не знаем и лишь теряемся в догадках. Не будем фантазировать.

— Может быть, вскоре нам удастся разузнать какие-нибудь подробности? — предположила моя жена.

— Вполне возможно, — ответил я, не подозревая, сколь близок мой ответ к истине.

Однажды я занимался, сидя в своем кабинете. Мой любимый предмет — математика — увлекал меня все больше и больше. В тот вечер я размышлял над одной сложной задачей, когда мне доложили, что меня спрашивает некий господин. Я попросил провести посетителя ко мне в кабинет. Им оказался стройный восьмиугольник, двигавшийся с непринужденным изяществом. Внешность его с первого взгляда располагала к полному доверию и внушала почтение. Велико же было мое удивление, когда посетитель представился доктором Пункто, недавно уволенным со своего поста директора Тригонометрической службы, чья неожиданная отставка вызвала столько кривотолков.

— Возможно, вы догадываетесь, — начал он, — что послужило причиной моего визита.

Что я мог ему ответить? Хотя кое-какие соображения на этот счет и мелькнули у меня в голове, однако высказывать их вслух я считал не вполне удобным: по моим предположениям посетитель пришел просить меня о помощи в связи со своей отставкой. Разве станет кто-нибудь, а тем более разумный и просвещенный восьмиугольник обращаться за советом к шарлатану и прорицателю и разве не был я в глазах широкой публики искушен в черной магии? Разве не считали мои недоброжелатели, что я знаюсь с нечистой силой? Мой посетитель не производил впечатление многоугольника, способного побеспокоить кого-нибудь по пустякам или ради праздной болтовни. Похоже было, что он решил (быть может не без влияния своей жены) прибегнуть к последнему средству.

Что ему от меня нужно? Может быть, он надеется, что с помощью волшебства я извлеку для него, из третьего измерения ту сумму денег, которую он растратил или потерял, и ему удастся таким способом оправдаться? Подобные мысли промелькнули у меня в голове, и я пребывал в растерянности, не зная, что ответить моему посетителю. По-видимому, он заметил мое смущение, потому что, немного помедлив, сказал:

— Вкратце дело, по которому я осмелился вас побеспокоить, сводится к следующему. Я пришел к вам за советом. Как вы, несомненно, слышали, меня уволили из Тригонометрической службы.

— Мне известно, — продолжал доктор Пункто, — что моя отставка породила множество самых нелепых слухов. Смею думать, однако, что вы придерживаетесь несколько иных взглядов на вещи, нежели широкая публика.

— Должен признаться, — ответил я, — что мне известен лишь сам факт вашей отставки. Относительно причин, вызвавших ее, я по сей день пребываю в полном неведении. Вам придется просветить меня на этот счет, чтобы я мог составить обо всем собственное мнение. Боюсь, однако, что не смогу ничем вам помочь.

Может быть, мои слова прозвучали несколько враждебно, но я умышленно избрал холодный тон. Я твердо решил без обиняков указать нежданному гостю на дверь, невзирая на его восемь равных сторон, если только он вздумает обратиться ко мне как к чернокнижнику и колдуну.

— Понимаю ваше недоумение, — сказал доктор Пункто. — Вы не усматриваете, каким образом могли бы мне помочь. К сожалению, я не могу ответить на ваш вопрос, ибо и сам ничего не знаю. Я хочу лишь предложить вашему вниманию некий комплекс загадок, путь к их решению для меня покрыт мраком. Я даже не знаю, в каком направлении его искать. Но если окажется, что эти загадки не под силу решить далее вам, то этого не сумеет сделать никто!

— В мире, я имею в виду в нашем двумерном Мире, — продолжал мой гость, подмигнув при этом, — есть немало математиков, но, думается мне, что здесь нашей старой, классической, математикой не обойтись. А поскольку вы показали, что способны не только воспринимать новые идеи, но и распространять усвоенные вами знания, то я решил: вряд ли кто-либо во всей Флатландии способен лучше вас беспристрастно разобраться в фактах.

— Если я правильно вас понял, — осторожно заметил я, — то ваш визит каким-то образом связан с чисто математическими проблемами и, следовательно, не имеет отношения к… гм… проблемам юридического и финансового порядка? Надеюсь, вы не рассердились на меня за то, что я задал вам столь прямой вопрос? — добавил я извиняющимся тоном.

— Наоборот, — воскликнул мой гость, — мне необычайно приятно опровергнуть слухи, распространяемые теми, кто не имеет ни малейшего представления о существе возникшей проблемы. Речь идет о чисто научной пли но крайней мере технической проблеме. Хотя я должен признаться, — добавил доктор Пункто, — что эта проблема носит весьма необычный характер.

Антипатия, которую я испытывал к неожиданному посетителю, бесследно исчезла. Я был захвачен таинственной проблемой, хотя и сам еще не сознавал этого.

— Позвольте спросить вас, — осторожно попытался выяснить я суть дела, — о чем, собственно, идет речь? Если об ошибках прикладных методов измерения и вычисления, то должен вас предупредить, что я не специалист и в технических вопросах не разбираюсь.

— Думаю, что интересующая меня проблема не имеет отношения к технике, а является чисто теоретической, — успокоил меня доктор Пункто. — Хотя не могу сказать этого с полной уверенностью. Знаю лишь одно: все в ней необычно, крайне необычно!

Взгляд бывшего директора Тригонометрической службы был устремлен куда-то вдаль. Я с сожалением подумал о том, что столь разумный человек, должно быть, поставил перед собой неразрешимую задачу, своего рода загадку, которой другие либо просто не замечают, либо считают не заслуживающей внимания. Желая хоть чем-то помочь ему, я заметил:

— А не лучше ли оставить все, как есть? Ведь не исключено, что интересующая вас проблема неразрешима…

— Неразрешима? — поспешил возразить он. — Нет, решение проблемы существует. Все имеет свои причины. Все имеет свое объяснение. Мне казалось, что вам как математику такая точка зрения должна быть особенно близка. Хотя объяснение порой бывает странным… очень странным!

— Можете рассчитывать на меня, — заверил я гостя. — Однако, чтобы я мог глубже понять проблему, постарайтесь изложить основные факты по возможности подробнее.

— Я бы предпочел не делать этого, — прямо заявил доктор Пункто. — Вы усомнитесь в моих наблюдениях, а может быть, и в моих умственных способностях. Не могли бы вы завтра отправиться со мной в одно место?

— Что же, я не против, — сказал я. — Наоборот, вы настолько заинтриговали меня, что мне просто не терпится познакомиться с проблемой поближе. Все же должен предупредить заранее: не исключено, что вас постигнет большое разочарование и я не смогу объяснить явление, при анализе которого вы встретили столь большие трудности.

— Во-первых, — начал перечислять свои контрдоводы доктор Пункто, — может случиться, что вам удастся обнаружить какую-нибудь ускользнувшую от меня ошибку, хотя я уверен в обратном. Если вы все же найдете ошибку и выяснится, что все решается просто, то я буду чрезвычайно признателен вам за участие. Если окажется, что мои наблюдения верпы и тем не менее нуждаются в объяснениях, то и в этом случае я останусь в выигрыше, ибо буду не один. С вами мы поделим трудности и сможем обсуждать их. Для меня это было бы огромной поддержкой. Во-вторых, не исключено, что вам удастся найти решение загадки. Итак, согласны ли вы мне помочь?

— Я уже сказал, — ответил я, — что ваше предложение необычайно заинтересовало меня. Я приложу все усилия, чтобы решить проблему, а в случае неудачи надеюсь, что вы не станете меня упрекать.

— Упрекать? — воскликнул мой гость. — Ни за что и никогда! Может быть, совместными усилиями нам удастся найти решение! Ум хорошо, а два лучше! К тому же, работая над одной проблемой, мы могли бы обсуждать ее и постепенно прийти к решению, хотя это и очень трудно.

— Могу я просить вас еще кое о чем? — задал я гостю последний вопрос. — Не намекнете ли вы, с какого рода задачей нам придется иметь дело?

— Охотно, — согласился доктор Пункто. — Не могли бы вы сказать, чему равна сумма углов треугольника?

Неожиданный вопрос озадачил меня, но я все же ответил:

— Разумеется, 180°.

— Всегда? — спросил доктор Пункто и с этими словами исчез за дверью.

Последнее замечание моего нового знакомого заставило меня призадуматься. Я разговаривал с ним довольно долго, у меня создалось впечатление, что это вполне разумный многоугольник, и вдруг этот вопрос, эти странные сомнения…

Можно ли быть уверенным в том, что на вопрос доктора Пункто в ста случаях из ста следует отвечать утвердительно? Всегда ли сумма углов треугольника равна 180°? Как можно усомниться в этом? Случалось ли кому-нибудь видеть треугольник с иной суммой углов? Как можно представить себе такой треугольник? Впрочем, доказать, что сумма углов треугольника равна 180°, совсем просто. Не лучше ли мне отказаться от участия в сомнительной затее моего нового знакомого? Потом отделаться от него будет гораздо труднее. А что если я попытаюсь разыграть из себя маньяка, одержимого какой-то другой бессмысленной навязчивой идеей, и заговорю с доктором Пункто о ней?

За этими размышлениями я провел бессонную ночь. Я намеревался придумать какую-нибудь отговорку, сослаться на неожиданный срочный вызов, в крайнем случае сказать, что умер кто-то из членов семьи, чтобы любым путем уклониться от встречи с тем, кто завтра с самого раннего утра будет стоять у моей двери. Однако стоило мне лишь увидеть вчерашнего гостя, как я вновь ощутил к нему такое доверие, что, не колеблясь, принял приглашение отправиться вместе с ним, о чем до сих пор не жалею.

Место, куда привел меня доктор Пункто, находилось за городской чертой. Наблюдательные пункты, расположенные на большом расстоянии друг от друга, образовали там триангуляционную сеть. Мы находились на наблюдательном пункте А. Оттуда при помощи новейшего прибора для измерения углов можно было определить углы между направлениями АВ, AC, AD, АЕ и AF. Мой провожатый попросил меня измерить угол между направлениями на пункты С и D. Я с удовольствием выполнил его просьбу, а заодно измерил и четыре остальных угла.

— Сумма всех пяти измеренных мной углов, естественно, должна быть равна 360°, — заметил я.

— Ну что же, проверим сначала сумму, — сказал мой новый друг (почему бы мне, в самом деле, не называть так доктора Пункто?).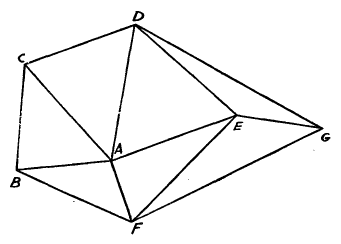

Мы сложили полученные величины углов и получили в результате величину, которая хотя и очень незначительно, но все же отличалась от 360°.

— Разумеется, ровно 360° не удается получить никогда, — заметил мой спутник, — ибо любое измерение, сколь бы тщательно мы его ни производили, неизбежно содержит некую малую ошибку. Она так и называется— ошибка измерения. Поэтому и сумма пяти измеренных углов никогда не бывает в точности равна 360°: она то меньше, то больше. У опытного наблюдателя отклонения меньше, у неопытного больше, но даже тот, кто производит измерения особенно тщательно, неизбежно совершает некоторую ошибку, хотя и очень малую.

— Об этом вы могли бы и не рассказывать, — заметил я. — Что существует ошибка измерения, мне хорошо известно.

— Тогда вам должно быть понятно, — продолжил свои объяснения мой собеседник, — что в том случае, когда одно и то же измерение приходится повторять несколько раз подряд, результаты получаются разными: одни больше, другой меньше.

— Разумеется, — согласился я, — но может случиться и так, что результаты нескольких последовательных измерений одной и той же величины окажутся одинаковыми…

— А затем, — подхватил мой друг, — снова появится меньшее или большее значение. И добавил:

— До сих пор все, о чем мы с вами говорили, было понятно. Вот теперь и начинается самое удивительное. Если мы перейдем в пункт С и измерим угол между направлениями CD и СА, а затем перейдем в пункт D и измерим угол между направлениями DC и DA и, наконец, вычислим сумму всех трех измеренных нами углов треугольника ACD, то…

— У нас должно получиться 180°, — закончил я фразу. — Вычисленная нами сумма окажется не в точности равной 180°, а будет отличаться от 180° либо в большую, либо в меньшую сторону на малую величину.

— Вы правы: так должно быть, — согласился мой друг, — но так не получается. Вычисленная мной сумма всегда оказывалась больше 180°, причем отклонение было слишком велико для того, чтобы его можно было приписать ошибкам измерения.

— Следовательно, — заключил я, — обнаруженное вами отклонение обусловлено не ошибками измерения и должна существовать более глубокая причина, по которой сумма углов треугольника ACD действительно больше 180°.

Я рассуждал здраво и логически безупречно, но все же, произнеся эти слова, невольно сам испугался их. Как это может быть? Что я, собственно, утверждаю? Сумма углов треугольника больше 180°! Но такое невозможно! Что делать, как быть?!

Доктор Пункто заметил мое замешательство. Он улыбнулся и сказал:

— Всё правильно! Именно к такому выводу пришел и я. Вы рассуждаете правильно, но… может ли быть такое? Нельзя же думать, что нам впервые удалось открыть треугольник, у которого сумма углов больше 180°! Такой вывод противоречит здравому смыслу. Такой вывод противоречит основам геометрии! Однако сумма углов оказывается больше 180° не только у треугольника ACD, но и у всех треугольников триангуляционной сети. В чем здесь дело, я не знаю. Может быть, вам удастся понять, чем вызван столь необычный результат? Может быть, вы можете хотя бы подсказать, в каком направлении следует искать решение этой загадки?

— Уж не послужило ли сделанное вами открытие причиной вашей отставки? — спросил я.

— Да, меня уволили именно из-за этого, — подтвердил доктор Пункто. — Отказались верить результатам моих измерений. Потребовали объяснений. Я рассказал все, о чем знал. Меня выслушали. Я видел, что многие смотрят на меня с сочувствием: либо я мошенник, либо душевнобольной. Сумма углов треугольника равна 180° и ничему другому. Но, клянусь святой Окружностью, я и сам знал об этом не хуже их! Мои судьи сочли, что, коль скоро я способен представить такие результаты измерений, мне никак не подобает занимать пост директора Тригонометрической службы.

— Но ведь здесь нет никакой подтасовки данных! — возмутился я.

— Мне особенно приятно слышать это от вас, — с достоинством заметил доктор Пункто. — По правде говоря, ничего другого я и не ожидал. Разумеется, мне не составляло никакого труда подтасовать результаты измерений так, чтобы скрыть обнаруженную невязку, но, совершив подобный подлог, я поступил бы против собственной совести.

— Кроме того, — добавил я, — не исключено, что впоследствии другой наблюдатель обнаружил бы расхождение между 180° и суммой измеренных углов треугольника и тогда ваш обман раскрылся бы.

— Вы правы, — такая возможность существует всегда, — признал доктор Пункто. — Нет, я действительно не мог поступить иначе.

— Есть еще один выход из создавшегося положения.

— Какой? — с интересом спросил доктор Пункто.

— Заявить, что ваши измерения были произведены с малой точностью и, следовательно, полученные результаты носят лишь приближенный характер. Тогда вопрос о невязке отпадает сам собой и все данные не будут противоречить геометрии.

— Такой выход действительно возможен, но лично, мне он претит. Я выполнил работу с величайшей тщательностью и представил результаты измерений, произведенных с величайшей точностью. Я не могу поступить иначе и считаю, что только так следует относиться к своим обязанностям.

— Полностью разделяю ваше мнение, — успокоил я доктора Пункто. — Я отношусь к исполнению своих обязанностей точно так же.

Наступило продолжительное молчание. Каждый из нас был погружен в свои мысли. Первым нарушил тишину я:

— Давайте подумаем над тем, что следует сделать в первую очередь. Я предлагаю как можно точнее исследовать обнаруженное явление.

Доктор Пункто с энтузиазмом воскликнул:

— Мой лучший друг! Не часто случается в жизни неожиданно обрести в зрелые годы настоящего друга. Друзьями в большинстве случаев становятся в юности, но я чувствую, что именно теперь у меня появился настоящий друг. Позвольте мне называть вас своим другом. Мой лучший друг! Не могу выразить, как я благодарен вам за ваше предложение, за вашу готовность помочь мне, за ваше согласие посвятить свое время и свой разум решению проблемы, затронувшей лично меня.

— Эта проблема затрагивает не только вас, — возразил я. — Речь идет о научной проблеме из области геометрии, которая меня чрезвычайно заинтересовала, Я охотно присоединяюсь к вам. Как два друга, мы совместными усилиями постараемся решить проблему, с которой вы столкнулись, или по крайней мере по возможности ясно и кратко изложим основные этапы своих поисков, чтобы впоследствии кто-нибудь мог воспользоваться нашими результатами.

— Позиция, достойная подлинного ученого! — одобрил мою речь доктор Пункто. — Вперед, за работу!

— Прежде всего, — попросил я, — объясните, почему обнаруженную вами невязку не замечали раньше. Относите ли вы это за счет погрешностей в прежних методах измерений или усматриваете причину в чем-то ином?

— Ответить на ваш вопрос очень просто. Существующие ныне методы измерений и новейшие приборы позволяют достичь большей точности, но нельзя отрицать и другое: отклонения суммы измеренных углов треугольника от 180° столь велики, что их вполне можно было обнаружить и раньше.

— А как, по-вашему, почему столь интересное явление все же оставалось незамеченным? Может быть, в этом проявилась боязнь признать странные, непопятные результаты измерений?

— Вполне возможно, — согласился доктор Пункто. — Признав правильность измерений, мы тем самым бросаем вызов тем, кто производил измерения до нас, а нам бы не хотелось делать этого без крайней необходимости.

— Займемся в таком случае поиском другой причины, — продолжал я. — Приводили ли прежние наблюдатели лишь округленные результаты измерений или выписывали столько десятичных знаков, сколько им удавалось получить?

— Я специально интересовался этим. У меня сложилось впечатление, что каждый наблюдатель приводил полученные им результаты с максимальной точностью, которой ему удавалось достичь. Тем не менее мне не довелось встретить ни одного упоминания о том, что величина суммы углов треугольника может быть значительно больше 180°. Малые же отклонения, естественно, можно приписать ошибкам измерения.

— Необходимо выяснить, в чем состоят различия между старыми и новыми методами измерений. Короче говоря, что не так или делается не так, как раньше?

— Между старыми и новыми методами измерений существует одно большое различие. Раньше измерения производили на маленьких, а теперь на больших треугольниках.

— Тогда нам прежде всего необходимо выяснить, как влияет на результаты измерений величина выбранных для триангуляции треугольников. Каким образом мы могли бы это сделать? Вы сейчас находитесь в отставке, следовательно, не можете производить изменения — у вас ист для этого пи приборов, пи помощников. А коль скоро это так, то не существует ли какого-нибудь иного способа раздобыть все необходимое?

— Надеюсь, — вздохнул доктор Пункто, — что мои бывшие сотрудники, когда я расскажу им, в чем дело, охотно согласятся произвести нужные измерения.

— Прекрасно, — сказал я. — Буду ждать вас у себя дома вместе с результатами измерений. Там мы сможем подробно обсудить наши дальнейшие планы.

Мы расстались как лучшие друзья. Я был убежден, что господин Пункто исполнит все пунктуальнейшим образом и в кратчайший срок, и не ошибся.

Прошла целая неделя, прежде чем мой друг Пункто навестил меня, чтобы обсудить полученные им данные. За это время он успел построить множество больших и малых треугольников и с высокой точностью измерить их углы. Сумма углов у больших треугольников неизменно оказывалась больше 180°, причем с увеличением размеров треугольника невязка возрастала. У маленьких треугольников отклонение суммы их углов от 180° было столь незначительным, что обнаружить его не удалось.

Немало часов я провел, проверяя выкладки доктора Пункто, по не нашел ни одной ошибки.

— Отсюда следует, — констатировал я, — что собранные вами факты можно считать твердо установленными и теперь мы вправе перейти к следующему этапу.

— Боюсь, что в дальнейшем ничем не смогу быть вам полезным, — огорченно заметил доктор Пункто. — Все по-прежнему выглядит весьма странно, и мы не располагаем ни малейшим намеком на то, в каком направлении надлежит искать объяснение.

— Без вас мы не сможем продвинуться ни на шаг, — заверил я его. — Прежде всего факты, объяснение придет потом. Мы на правильном пути, и я не сомневаюсь в том, что в конце концов нам удастся найти истину.

Мы сидели до поздней ночи, перебирая всевозможные гипотезы, но безрезультатно. Случай был поистине удивительный! Мы условились, что до следующей встречи, назначенной через три дня, каждый из нас попытается самостоятельно обдумать факты, после чего мы обменяемся идеями. Даже в том случае, если они окажутся неудачными, ошибка одного вполне может навести другого на верную мысль. Мы сердечно распрощались и расстались в полной уверенности, что совместными усилиями найдем выход из лабиринта.

Излишне говорить о том, что все три дня я провел в напряженных размышлениях. Ежедневно, прежде чем заснуть, я подолгу обдумывал проблему в надежде увидеть во сне какую-то подсказку, которая бы помогла ее решить или хотя бы направила поиски решения по правильному пути. Но все было напрасно. Днем я пытался выстроить в логической последовательности все известные мне факты, но каждый раз заходил в тупик: логика была бессильна найти ответ на столь «нелогичный» вопрос. Погруженный в свои размышления, я забыл обо всем на свете. Перед моим мысленным взором мелькали разнообразнейшие треугольники: большие и маленькие, правильные и неправильные, тупоугольные и остроугольные. Каждый из них я обходил по периметру, измерял все углы и принимался за следующий.

Мои близкие, не желая мне мешать, и не пытались пробудить меня от грез наяву. Но порой мне случалось ловить на себе их удивленные взгляды. Я не слышал, когда ко мне обращались, и в ответ неизменно задавал один и тот же сакраментальный вопрос: «Не могли бы вы указать треугольник, у которого сумма углов больше 180°?»

На утро третьего дня (того самого, на который у меня была назначена встреча с моим другом Пункто) ко мне в кабинет заглянул мой внук.

— Дедушка, — сказал он, — не знаю, смогу ли я помочь тебе, но вчера ты все время спрашивал о треугольнике, сумма углов которого больше 180°.

— Да, — подтвердил я, — и мне хорошо известно, о чем ты сейчас думаешь. Ты, естественно, считаешь, что твой старый дедушка выжил из ума. Я и сам прекрасно знаю, что мой вопрос звучит бессмысленно, но это, поверь мне, далеко не так. Я пытаюсь найти ответ на один вопрос и не знаю толком, математический он или философский, а для того чтобы найти ответ, мне необходимо своим глазом увидеть треугольник, у которого сумма углов была бы больше 180°.

— Дедушка, — воскликнул мой внук, — я прекрасно понимаю, что какой бы обычный треугольник мы ни взяли, сумма его углов не будет отличаться от суммы углов любого другого обычного треугольника. Треугольник, который нужен тебе, должен быть необычным треугольником, ибо лишь у необычного треугольника может быть необычное свойство. Если ты разрешишь, я нарисую один такой треугольник.

Хотя я не возлагал особых надежд на помощь со стороны представителя младшего поколения, тем не менее мой утвердительный ответ на его просьбу был продиктован не только любовью к внуку, но и любопытством: мне не терпелось узнать, что за необычный треугольник выдумал мой внук. Мальчик был очень польщен, увидев, что дед проявляет к его открытию искренний интерес, и тотчас же принялся рисовать «необычную» фигуру.

— Дедушка, вот треугольник, у которого сумма углов больше двух прямых углов.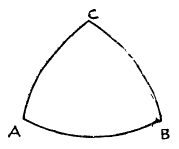

— Да, но у твоего треугольника стороны не прямые, — возразил я.

— В этом и заключается мое открытие, — заявил юный геометр. — Нужно же было придумать нечто необычное для того, чтобы ответить на необычный вопрос.

— Что касается необычности, то тут мы квиты, — вынужден был признать я. — Но должен тебе сказать, что до сих пор мне никогда не приходилось видеть треугольники с кривыми сторонами.

— А ты в этом уверен? — спросил мальчуган.

Услышав вопрос внука, я даже рассердился. Мне ли не быть уверенным! Производя измерения на местности, мы даже не проводили стороны треугольников, а провешивали с помощью измерительных приборов прямые, вдоль которых свет распространялся от одного наблюдательного пункта к другому, а свет, как известно, распространяется вдоль прямых. На этом все и основано!

Разумеется, я не стал выказывать признаков недовольства, ибо меня очень обрадовало, что мой внук изъявил желание помочь мне. И хотя его «необычный треугольник» не позволил мне продвинуться ни на шаг дальше, он все же отвлек меня от безрадостных мыслей, от безнадежно запутанных рассуждений, в которых я беспомощно блуждал по замкнутому кругу, не видя выхода. Вечером придет мой друг. Мы обсудим с ним загадочную проблему, к которой я по-прежнему не знаю, как подступиться. Может быть, ему удалось придумать нечто новое?

Мои надежды на то, что господину Пункто удалось набрести на какую-нибудь удачную идею, оказались напрасными. По его словам, он все три дня провел в размышлениях над проблемой, но, насколько я понял из его объяснений, во всем, что касалось поиска решения, всецело положился на меня. Доктор Пункто считал, что я, внук знаменитого Квадрата, должен обладать незаурядными способностями и уметь решать самые необычные проблемы, в особенности те, перед которыми бессильна традиционная геометрия. Хотя столь высокое мнение о моих способностях не могло не польстить мне, я все же был несколько раздосадован тем, что доктор Пункто занимался проблемой, если можно так выразиться, «не в полную силу». Я высказал ему свое недовольство, но он со смехом упрекнул меня в том же, и мне не оставалось ничего другого, как признать, что не имею ни малейшего представления, в каком направлении надлежит продолжать поиски решения. Я не мог похвастаться ни тем, что мне известен правильный подход к решению проблемы, ни даже тем, что знаю, как хотя бы немного продвинуться к цели.

— О решении говорить преждевременно, — сказал мой гость. — Пути к нему мы выясним позже. Пока же нам требуются самые необычные идеи, которые позволят построить треугольники со свойствами, отличными от привычных нам свойств треугольников. В построении таких треугольников — один из возможных шагов на пути к решению интересующей нас проблемы. Если бы мне удалось придумать такую фигуру, что ее хотя бы с известной натяжкой можно было назвать треугольником и сумма ее углов при этом была бы больше 180°, то я считал бы выход из тупика, в котором мы находимся, найденным. Однако, как я ни старался, мне так и не удалось придумать фигуру, обладающую нужными, свойствами.

— Да, — вынужден был признать я, — ваша точка зрения вполне приемлема. Но коль скоро все упирается в построение «треугольника» с нужными свойствами, то у меня для вас кое-что есть.

С этими словами я предъявил доктору Пункто треугольник с изогнутыми сторонами, который нарисовал мне мой внук.

Пункто внимательно выслушал меня, тщательно осмотрел треугольник с криволинейными сторонами и… не засмеялся! После длительного молчания он произнес:

— Может быть, это первый шаг к решению. Сумма углов данного треугольника действительно больше 180°. В этом смысле задача решена. Вопрос лишь в том, допустимо ли рассматривать треугольники с изогнутыми сторонами.

— Разумеется, недопустимо, — заметил я несколько раздраженно. — Ведь если я не ошибаюсь, свет распространяется вдоль прямых.

— Вы совершенно нравы, — невозмутимо ответил Пункто. — Найдено решение лишь частичной проблемы, по оно может оказаться ложным.

Мы еще долго, на протяжении нескольких часов, обсуждали проблему, но безрезультатно. Прощаясь со мной, доктор Пункто сказал:

— Попробуем кратко сформулировать, как нам представляется положение вещей в данный момент. Из наблюдений нам известно, что сумма углов треугольников, измеренных на местности, не равна 180°, а больше 180°, причем невязка возрастает с увеличением размеров треугольника. У треугольников больших размеров она больше, чем у треугольников меньших размеров. Это во-первых. Во-вторых, можно предполагать, причем без особой уверенности, что подобная невязка встречается у треугольников, стороны которых не прямолинейны.

— Таков печальный итог наших размышлений, — подтвердил я.

— Итог не окончательный, — оптимистически заметил доктор Пункто.

— Что нам делать дальше? — спросил я. — Снова три дня предаваться размышлениям в ожидании, что кому-нибудь из нас придет в голову еще одна удачная идея? Окажется ли она удачнее первой?

— Да, такая перспектива не слишком привлекательна, — согласился доктор Пункто. — По-видимому, нам лучше поговорить с другими людьми и посмотреть, как они будут реагировать на идею о криволинейных треугольниках.

— Не обратиться ли за советом к моему внуку? — саркастически произнес я. — Мне кажется, что это лучший способ беспредельно раздуть тщеславие мальчишки.

— Я с большей охотой послушал бы, — сказал мой друг, — как реагируют на интересующую нас проблему ученые мужи, в особенности математики. Нельзя ли заинтересовать их? Мы располагаем фактами, требуется найти их научное объяснение.

— Или опровергнуть эти факты, — добавил я.

— Думаю, что опровергнуть их невозможно, — возразил доктор Пункто, и я не мог с ним не согласиться, поскольку результаты измерений действительно были безупречны.

Нам казалось, что лучше всего привлечь к интересующей нас проблеме внимание членов физико-математического факультета нашего университета. Я вызвался разыскать математиков и физиков, которые бы выразили готовность ознакомиться с проблемой.

Вопреки ожиданиям я без труда справился со своей задачей. Я думал, что факультет поручит кому-нибудь из специалистов выслушать наши «свидетельские показания» по поводу необычайных событий, но все вышло иначе. Доктора Пункто и меня пригласили на собрание всего факультета, с тем чтобы мы могли изложить там свои взгляды.

В назначенное время мы в отличном расположении духа отправились на высокоторжественный форум, но, войдя в зал, почувствовали себя, как подсудимые перед началом разбирательства. Мы не могли отделаться от ощущения, что пригласили нас лишь для того, чтобы, пользуясь удобным случаем, пресечь распространяемую нами ересь, осудив ее в официальном решении общего собрания факультета. Это ощущение не покидало нас на протяжении всего заседания.

Сначала председатель предоставил слово доктору Пункто, назвав его «бывшим землемером». Доктор Пункто не без сарказма исправил ошибку председателя, сказав, что в настоящее время он имеет честь носить звание «бывшего главного землемера, эксдиректора Центральной Тригонометрической службы». Председательствующий реагировал на это замечание лишь краткой фразой «Вам слово», после чего доктор Пункто спокойно, строго придерживаясь фактов, рассказал обо всем, что произошло. Он сообщил собравшимся, что, согласно проведенным под его руководством измерениям, сумма углов треугольника оказалась больше 180°, причем отклонение от 180° тем больше, чем крупнее размеры треугольника. Никогда ранее, подчеркнул он, такое отклонение не наблюдалось, поскольку в прежние времена измерения производились на маленьких треугольниках и упомянутое выше отклонение превышало ошибки измерений. Доктор Пункто заявил, что отбрасывать серию произведенных под его руководством измерений на том лишь основании, что они приводят к парадоксальному выводу, не следует, ибо, по его мнению, необходимо попытаться найти научное объяснение столь странному явлению.

После того как доктор Пункто ясно и понятно изложил все имевшиеся в нашем распоряжении факты, слово попросил ученый-математик по имени Эрго. Путем весьма длинных и сложных рассуждений он доказал, причем вполне правильно, что наука, вообще говоря, призвана заниматься поиском объяснений экспериментально наблюдаемых фактов, а факты, о которых упоминал в своем выступлении доктор Пункто, такого рода, что науке следует незамедлительно отказаться от их рассмотрения. Сумма углов любого треугольника равна 180°, или двум прямым углам. Это доказали еще в глубокой древности, поэтому каждому ясно, что сумма углов треугольника не может принимать другое значение. А коль скоро некая серия измерений приводит к противоречию с одним из основных принципов науки, то эта серия измерений ошибочна. Ученые не обязаны заниматься поиском ошибок. Это должны сделать сами наблюдатели, допустившие вопиющую небрежность! Факультет не должен заниматься столь недостойным делом. Принять участие в подобной затее означало бы нанести ущерб престижу факультета.

Затем слово взял ученый-физик профессор Суппосо. Мы сразу же почувствовали, что выступает человек совсем другого склада. Профессор Суппосо все свое выступление построил на том, что в естественных науках, и в частности в физике, нередко приходится иметь дело со странными на первый взгляд результатами, которые при ближайшем рассмотрении оказываются верными. По его мнению, задача физики в том и состоит, чтобы отыскивать факты, кажущиеся невероятными, и затем пытаться найти им объяснение. Факты, приведенные доктором Пункто, весьма необычны, продолжал свои рассуждения профессор Суппосо, ибо они затрагивают основы основ математики, но тем не менее мы должны отнестись к ним с величайшей благосклонностью. Нам следует задать себе вопрос: можем ли мы представить себе треугольник, у которого сумма углов была бы больше 180°? Никогда еще нам не доводилось видеть такой треугольник ни в действительности, ни в воображении. Следовательно, чтобы обладать столь необычайными свойствами, сами треугольники должны быть весьма необычными. Может ли кто-нибудь из присутствующих опрокинуть существующие многократно проверенные научные представления и указать нам или начертить такой треугольник? Если никто не в состоянии сделать это, то я считаю вопрос исчерпанным. Однако если кому-нибудь все же удастся построить такой треугольник, то я с радостью приму участие в дальнейшем обсуждении.

Ободренный выступлением профессора Суппосо, я попросил слово и, когда мне его предоставили, произнес следующую речь:

— Уважаемые господа, высокоученые члены прославленного факультета! Позвольте мне высказать одно-единственное замечание по поводу выступления предыдущего оратора. Я в состоянии начертить треугольник, обладающий требуемым свойством. Предыдущий оратор уже отметил, что этот треугольник должен быть странным, необычным. Вот я и намереваюсь продемонстрировать вам треугольник не с прямолинейными, а с криволинейными сторонами, у которого сумма углов больше 180°.

На какое-то мгновение в зале воцарилась тишина. Пользуясь паузой, я начертил криволинейный треугольник.

— Позволю себе заметить, — возразил господин Эрго, — что свет в нашем мире распространяется вдоль прямых и поэтому стороны треугольников, используемых при триангуляции, не могут быть искривленными.

Шум в зале мгновенно стих, когда слово вновь попросил Суппосо.

— Господин председатель, — сказал он, — я решительно не согласен с тем, что здесь только что утверждалось. Мы могли бы принять гипотезу о том, что свет распространяется не прямолинейно, а криволинейно, но, прежде чем совершить такой шаг, необходимо выяснить, не противоречит ли такая гипотеза другим явлениям. У меня подобная гипотеза вызывает возражение по совершенно иной причине. Рассмотрим любые два треугольника в триангуляционной сети, имеющие общую сторону, например треугольники ABC и BCD. Для того чтобы сумма углов треугольника ABC была больше 180°, сторона ВС должна быть изогнута наружу, то есть вправо. Но треугольник BCD должен обладать тем же свойством, что и треугольник ABC. Сумма углов этого треугольника также должна быть больше 180°, то есть сторона ВС должна быть изогнута влево. Ясно, что сторона ВС в одно и то же время не может быть изогнута и вправо, и влево. Следовательно, объяснение, предложенное нашим гостем, несостоятельн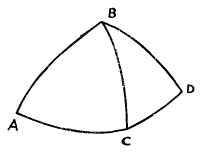о.

В ответ на это замечание я не мог возразить решительно ничего. Рассуждения Суппосо казались мне столь обоснованными, что я готов был отказаться от своей гипотезы. Больше сказать нам было нечего, ибо у моего друга Пункто также не осталось в запасе ни одного аргумента.

С притворным сочувствием и скрытой издевкой председательствующий подвел итог дискуссии:

— Вы видели, господа, что факультет не жалел ни сил, ни времени для рассмотрения вашей проблемы, но безрезультатно. Вам не остается ничего другого, как попытаться самим найти ошибки в произведенных вами измерениях. Ученые не могут тратить время на решение подобных вопросов. Факультет требует лишь, чтобы вы осознали свои заблуждения, не пытались за нашей спиной упрекать ученых в недостаточно доброжелательном отношении к вам и не выставляли нас в ложном свете. Если же вы не внемлете нашему дружескому предостережению, мы незамедлительно примем меры, дабы восстановить справедливость, и привлечем клеветников к ответу. Не смею вас больше задерживать, господа!

Ни один из нас не нашел, что ответить. Мы покинули зал и побрели к дому. На душе было скверно. Мы проиграли сражение. И все же нашим противникам не удалось убедить нас в том, что мы неправы. Наоборот, все факты были в нашу пользу, и науке рано или поздно придется найти им объяснение. Я пригласил доктора Пункто зайти ко мне, чтобы обсудить дальнейшие планы.

Войдя в мой кабинет, мы вновь почувствовали себя легко и непринужденно. Враждебный мир был где-то далеко за его стенами. Мы долго сидели, погруженные в свои мысли, пока доктор Пункто не нарушил молчания. В его словах снова прозвучал присущий ему неисчерпаемый оптимизм.

— Встреча с учеными, — заметил он, — оказалась все же небесполезной. Эрго, человек старой закалки, просто отбрасывает все, что ему непонятно, но Суппосо сказал гораздо больше, и кое над чем из его рассуждений нам следовало бы подумать. Суппосо хотел бы увидеть треугольник, обладающий необычными свойствами. В случае необходимости он готов даже довольствоваться треугольником с изогнутыми сторонами. Его не устраивает лишь направление, в котором изогнуты стороны треугольника, ибо оно приводит к противоречию. Я не знаю, каким образом мы сможем преодолеть эту трудность, поскольку рассуждения Суппосо мне кажутся безупречными. Если какая-то линия не может быть изогнута ни влево, ни вправо, то она вообще не может быть изогнута, поскольку другого направления, в котором она могла бы изогнуться, не существует.

— Ни влево, ни вправо, а другого направления не существует, — повторил я вслед за доктором Пункто. — Другого направления не существует… Впрочем постойте! Мы просто привыкли думать, что другого направления не существует. Его лишь нельзя наглядно представить себе, но оно существует. Это недоступное непосредственному созерцанию направление перпендикулярно нашему миру. Линии могут казаться нам прямыми, но в действительности быть незаметно для нашего глаза изогнутыми в третьем направлении! Так вполне может быть! А в нашем случае просто не может быть иначе!

— Я не вполне понял то, что вы сейчас сказали, — произнес доктор Пункто, — но если интуиция меня не обманывает, вы видите некое решение проблемы.

— «Вижу» — не то слово, — поправил я своего друга. — К сожалению, я не вижу решения, ибо мне не дано его видеть, но разумом понимаю, каким оно должно быть. Позвольте мне еще немного поразмыслить, а завтра мы продолжим разговор.

На этом мы расстались. Настроение у нас обоих было отличное.

Быть может, ночь принесет окончательное решение или хотя бы направит мои мысли в нужную сторону? Ведь ночью во сне нам часто приходят в голову такие логические ходы, до которых мы никогда не додумались бы наяву!

Я возлагал на ночь большие надежды. Ошибиться было невозможно: истина где-то рядом. Правильное решение было теперь настолько близко, что мой разум мог совершить последний шаг и во сне. Я счел полезным еще раз мысленно перебрать основные пункты своих рассуждений. Итак, что мы имеем? Я должен воочию представить себе треугольник, у которого сумма углов больше 180°. Стороны такого треугольника не могут быть прямыми. Они должны быть изогнутыми, непременно изогнутыми, не влево и не вправо, по изогнутыми! Не представляю! Не могу представить! То, что не изогнуто ни вправо, ни влево, но все же изогнуто, мне просто не дано видеть. Стороны такого треугольника изогнуты в некоем невидимом направлении. Изогнуты в невидимом направлении! Как это? Можно ли мысленно представить себе направление, недоступное непосредственному созерцанию? Да, конечно! В нашем мире есть два направления, но Сфера спускается к нам по третьему, не видимому для нас, но вполне видимому для нее направлению, перпендикулярному нашему миру. Не могут ли стороны треугольника быть изогнутыми в третьем, не видимом для нас направлении?

Для нас, живущих в двумерной Флатландии, такое искривление было бы совсем незаметно. Это проще понять, рассмотрев мир одного измерения — Лайнландию. Может ли там существовать некое искривление, не видимое ее обитателям, но заметное для нас?

И тут я увидел перед собой Лайнландию, но не прямую, а изогнутую в виде огромной окружности! Собственно говоря, это была уже не Лайнландия, а Циркульландия! Взгляните! Ее обитатели движутся то в одну, то в другую сторону, но не в силах сойти со своей окружности. Сколько самоуверенности слышится в их жужжании. Ха, а вот и король!

— Сир! — обратился я к монарху. — Ваше величество! Выслушайте меня!

— Кого это я должен выслушивать? — возмутился король. — Я никого не вижу. Уж не того ли злого волшебника, который несколько лет назад поставил под угрозу самое существование моего государства, но успел вовремя скрыться? Пусть он лучше не попадается мне на глаза! Я ему покажу!

— Ваше величество! — произнес я. — Я то самое лицо, о котором вы говорите, но я не только не злой, по даже и не волшебник. Я пришел к вам из мира двух измерений.

— Нет, вы только послушайте, что, говорит этот призрак, дух или кто бы он там ни был! Мир двух измерений? Но ведь существует лишь один мир, и он имеет лишь одно измерение. Это мой мир, я правлю им как король и не потерплю возражений ни от моих подданных, ни от кого другого, будь он призрак, дух или волшебник!

— Да послушайте же вы, могущественный владыка! — попытался я прервать короля.

— Вот это обращение по крайней мере учтиво, — откликнулся король. — Я господин и повелитель всего мира, и, естественно, мое могущество беспредельно. Что вам от меня нужно? Уж не хотите ли вы снова завести разговор о другом мире, откуда вы якобы явились? Пустая болтовня! Меня вы не проведете.

— Нет, на этот раз я хотел бы поговорить с вами о вашем собственном мире, — сказал я.

— Прекрасно, — обрадовался король. — Я постараюсь вам как можно понятнее рассказать, как выглядит мой мир. Мне ли не знать его! У вас, насколько я мог понять, совершенно превратные представления о моем мире.

— Слушаю вас, ваше величество.

— Все очень просто, — начал король и добавил менее любезно: — По крайней мере для того, у кого есть разум.

— Слушаю вас внимательно, — произнес я, делая вид, будто не заметил монаршей колкости.

— Мой мир, — начал король, — единственный и неповторимый, ибо другого просто нельзя себе представить. Где разместился бы другой мир? Для него просто не остается места…

— Где же в таком случае нахожусь я? — пришлось мне прервать королевскую речь. — Разве не вне вашего мира?

— Где вы и откуда появились, я не знаю, — сказал король. — Может быть, вы вообще не существуете и лишь снитесь мне.

— Разве вы забыли, как однажды я слегка дотронулся до ваших внутренностей? — спросил я. — Ведь коснуться их может лишь тот, кто приближается к вашему миру извне. Если угодно, я могу повторить.

— Глупости, — сердито заметил король. — У человека всегда может быть приступ колик. Из этого вовсе не следует, что кто-то непременно должен был дотронуться до его внутренностей извне, из другого мира. Чушь!

— Хорошо, не будем спорить. Расскажите мне лучше, какую форму имеет ваш мир.

— Форма! Форма! Какая бывает форма? Каждое существо может быть длиннее или короче. Как, по-вашему, существа разной длины имеют различную форму? Все существа, независимо от их размеров, находятся в бесконечно большом мире, ибо наш мир беспредельно велик. В обе стороны он простирается до бесконечности.

— Позвольте задать вам еще один вопрос, уважаемый король. Откуда вы знаете, что ваш мир бесконечно велик?

— Странный вопрос! А как может быть иначе? Коль скоро мир возник в одном месте, что может помешать ему распространяться дальше и дальше? Ведь прямую, сколько ни продолжай, всегда можно продолжить еще дальше, причем неограниченно далеко. Это и есть то, что принято называть бесконечностью.

— А каким образом вы умудряетесь получать сообщения от существ, находящихся от вас бесконечно далеко? Смогли бы вы получить хотя бы один сигнал, свидетельствующий о том, что и в бесконечности есть жизнь?

— Нет, разумеется, нет! Но поскольку у вас есть разум и вы наделены хотя бы некоторой способностью рассуждать логически, то вам все будет понятно. Хотя мир простирается до бесконечности, ниоткуда не следует, что и в бесконечности он обитаем. Даже если бы мы предположили, что на бесконечно большом удалении от нас обитают живые существа, то мы все равно не смогли бы заметить никаких признаков жизни, ибо испускаемые ими вопли дошли бы до нас через бесконечно большой промежуток времени. Кроме того, с увеличением расстояния громкость звука слегка ослабевает. Существует определенная граница, за которой мы перестаем слышать звук. Если вы наделены разумом, то сказанного мной достаточно для того, чтобы у вас создалось представление о том, как выглядит мир. Есть ли у вас еще вопросы ко мне, незнакомец?

— Вопросов больше нет, — ответил я, — зато мне хотелось бы кое-что вам сообщить. Во-первых, я хотел бы заметить, что ваш мир не прямой, а искривленный. Во-вторых, ваш мир не бесконечен, а конечен. По форме он совпадает с фигурой, которую мы, флатландцы, называем окружностью.

— Каким образом, — перебил меня король, — мир может не быть бесконечным? Даже если он ограничен, то должно же быть что-то и за границей мира?

— Ваш мир не бесконечен, — поучительно заметил я, — но он неограничен. Ваш мир образует замкнутую кривую, которая не имеет ни конца, ни начала. Если бы другие обитатели вашего мира не стояли у вас на пути и вы могли бы беспрепятственно двигаться в одном и том же направлении, то спустя некоторое время вы вернулись бы на исходное место.

— Не понимаю, как это может быть, — признался король.

— Здесь-то как раз все ясно, — возразил я, — впрочем, я вас не виню. Ваш мир конечен, поскольку представляет собой окружность — замкнутую кривую.

— Неужто мир искривлен? — спросил король. — Трудно в это поверить!

— Представить себе искривленный мир вы действительно не в силах. Ваш линейный мир искривлен в направлении, которое недоступно вашим ощущениям, ибо оно перпендикулярно вашему миру. Если бы кривизна была значительнее, а мир соответственно очень маленьким, то вы могли бы наблюдать замечательное явление, не уходя для этого далеко от своего «насиженного» места: звук следовал бы вдоль вашего мира, то есть распространялся бы вдоль кривой.

— Мне иногда кажется, что вы нарочно несете несусветную чушь, — сказал король. — Звук следовал бы вдоль нашего мира… А как ему еще следовать? Вы называете это «распространением вдоль кривой». Какая нелепость! Просто невероятно! Кроме того, я не понимаю, что означает слово «кривая». Любой мальчишка в Лайнландии объяснит вам, как происходит распространение звука в действительности.

— Звук в вашем мире распространяется не по кратчайшему пути, — попытался объяснить я. — Точнее говоря, путь, по которому он распространяется, является кратчайшим из возможных в вашем мире, но действительно кратчайший путь лежит за пределами вашего мира.

— Я снова вас не понимаю, — заявил король.

— А между тем это просто, — возразил я, — но не могу же я требовать от вас, чтобы вы поняли то, что не. можете себе представить. Не думаю, чтобы вы могли почерпнуть многое у меня, но я узнал от вас чрезвычайно много полезного.

— Вот уж чего никогда бы не сказал, судя по тому, что вы говорите, — не остался в долгу король.

— Вам этого не понять, — произнес я и исчез, или, лучше сказать, Циркульландия расплылась и скрылась во мраке ночи.

Я проснулся. Привидевшаяся мне во сне страна не давала покоя. Она была искривлена в направлении, которое обитатели одномерного мира не могли воспринимать, поскольку оно проходило перпендикулярно их миру.

Не так ли обстоит дело и с нашим двумерным миром? Может быть, стороны треугольников, которые кажутся нам прямыми, искривлены в третьем, не видимом для нас направлении? Такое искривление можно представить себе лишь мысленно, поскольку увидеть его своими глазами нам, флатландцам, не дано. Вот если бы попасть в третье измерение! Единственная возможность убедиться в искривленности треугольников — спросить об этом у Сферы, когда та навестит нас в следующий раз.

Я решил непременно это сделать.

Я еле дождался следующей встречи с доктором Пункто. Разумеется, он сразу понял причину моего хорошего настроения и спросил:

— Вам удалось найти решение?

— Нет, — ответил я, — кричать «Эврика!» еще рано, но я убежден, что мне удалось вплотную приблизиться к источнику наших затруднений. Странное явление, состоящее в том, что сумма углов треугольника больше 180°, можно, как я полагаю, объяснить, приняв следующее предложение. Стороны треугольника искривлены, но их кривизна незаметна. Подчеркиваю, незаметна для нас. Стороны треугольника искривлены в направлении, перпендикулярном нашему миру. Трехмерное существо может без труда это заметить. Нам, обитателям двумерного мира, сие не дано.

Затем я рассказал доктору Пункто о том, как во сне увидел Лайнландию, изогнутую в форме окружности, и как тамошний король не мог понять, что его мир искривлен.

— Вот если бы нам удалось разузнать об истинном положении вещей у какого-нибудь обитателя трехмерного мира, — мечтательно произнес доктор Пункто.

Это замечание навело меня на мысль пригласить моего друга к себе на встречу Нового года, где мы можем рассчитывать на свидание со Сферой.

Я посоветовался с женой, она не только не возражала, но и горячо одобрила мой план. Ведь встреча Нового года — праздник, который принято проводить в кругу семьи, предаваясь размышлениям о семейных радостях и невзгодах. Почему бы нам не пригласить на него нашего нового друга, чтобы не чувствовать себя духовными париями, изгнанными из научных кругов?

Старый год подходил к концу. Последние его недели показались мне месяцами, последние дни — неделями, но наконец наступил предновогодний вечер. Вся моя большая семья была в сборе: моя жена и я, дети и внуки. Пришел к нам и доктор Пункто. Его спокойная, уравновешенная натура, присущая ему непринужденная манера общения покорили всех, и мы чувствовали себя так, словно наша семья пополнилась еще одним членом.

Вечер прошел очень оживленно. Разумеется, я рассказал сказку, затем мы отведали окружностей, испеченных на масле. Время подошло к двенадцати, и мы принялись с нетерпением ожидать, когда пожалует Сфера. Для нашего гостя было непривычно созерцать ее появление: крохотная окружность раздувается, разрастается и наконец достигает максимальных размеров.

После обычного обмена приветствиями я позволил себе подчеркнуть, что нынешний визит Сферы мы ожидали с особым волнением, поскольку доктор Пункто и я столкнулись с важными проблемами, которые нам, по-видимому, удалось успешно решить. Однако подтверждение правильности наших предположений кем-нибудь из обитателей Трехмерия было бы чрезвычайно желательным.

Я начал свой рассказ. Сфера слушала меня с неослабным вниманием. Я упомянул о тех трудностях, с которыми столкнулся доктор Пункто при измерении углов треугольников. Чтобы подчеркнуть всю важность и необычность выводов, сделанных доктором Пункто из результатов наблюдений, я подробно остановился на злоключениях, выпавших на долю ученого. Затем я рассказал Сфере, какое объяснение придумали мы странному явлению, состоящему в том, что в нашем пространстве сумма углов треугольника оказалась больше 180°. Мы предположили, что стороны треугольника не прямолинейны, а искривлены, причем в направлении, перпендикулярном нашему пространству, в силу чего кривизна сторон незаметна наблюдателям-флатландцам.

Когда я закончил свой обзор, доктор Пункто счел необходимым сообщить нашему трехмерному гостю, что честь открытия столь необычайного решения всецело принадлежит мне. В свою очередь я воздал должное заслугам доктора Пункто. Именно он первым осознал, что обнаруженная невязка не принадлежит к числу случайных ошибок и имеет под собой геометрическую основу.

Нас очень интересовало, что скажет по поводу нашего сообщения Сфера. Довольно долго та молчала. Я понял, чем заняты мысли нашего гостя: он обдумывал, как в своих рассуждениях обойти ряд трудностей, которые для нас, двумерных существ, были значительно серьезнее, чем для обитателей трехмерного пространства. Когда Сфера начала свой рассказ, нам было необычайно приятно отметить, что она поняла и природу наших затруднений, и самый ход нашего решения.

— Более того, — заявила Сфера, — ваше решение абсолютно верно. Еще раз, находясь среди вас, я подумала о том, что настало время сообщить вам более подробные сведения о форме вашего пространства, но потом у меня возникли опасения: мне не хотелось без особой необходимости насильно перестраивать ваши основные геометрические представления. Теперь я могу рассказать вам, что ваш мир, двумерное пространство, не плоский, а искривленный. Я хотела бы также объяснить вам, что это означает. Внешне ваш мир выглядит не как ровная, а как изогнутая поверхность. К сожалению, ограниченность вашего двумерного восприятия не позволяет вам представить наглядно эту картину.

— Нам понятно, о чем вы говорите, — заверил я Сферу. — Обитателю Лайнландии неизвестно, имеет его мир форму прямой или кривой, потому что лайнландец лишен способности воспринимать направление, в котором искривлен его мир. Поэтому вполне может быть, что одномерная Лайнландия в действительности имеет форму окружности и, следовательно, обладает не бесконечной, а лишь конечной протяженностью, хотя и безгранична, то есть не имеет границ, или конечных точек.

— Совершенно верно, — обрадовалась Сфера. — Пользуясь случаем, замечу, что и ваш мир устроен аналогично: он не плоский, а искривленный. Вы живете не на бесконечно протяженной плоскости, а на поверхности большой сферы.

— Не могли бы вы рассказать об этом подробнее? — попросил доктор Пункто.

— Охотно, — согласилась Сфера и продолжала: — Вы знаете и понимаете, что окружность ограничивает некую часть двумерного пространства, а сама является одномерной кривой. Аналогично в Трехмерии сфера, трехмерное тело, ограничена двумерной поверхностью, которая так и называется — поверхность сферы.

— Аналогию можно продолжить, — добавил я. — Гиперсфера, четырехмерное тело, ограничена трехмерной гиперповерхностью.

— Вы, безусловно, правы, — согласилась Сфера, — хотя я не могу представить себе это наглядно так же, как вы — поверхность сферы.

— Итак, — вступил в беседу доктор Пункто, — если я правильно понял, наше пространство искривлено, всюду искривлено, хотя мы этого не замечаем?

— Совершенно верно, — подтвердила Сфера, — так же как искривлена всюду окружность, хотя обитающие на ней лайнландцы не ощущают искривленности своего пространства.

— Но мы же заметили кривизну своего пространства, — отважился заметить я.

— И да, и нет, — ответила Сфера, — Искривленности своего пространства вы бы никогда не заметили, да и не могли заметить. Вы обратили внимание лишь на одно из следствий, к которому приводит кривизна, но и то случайно. Поскольку ваше двумерное пространство искривлено и, следовательно, не является плоским, то сумма углов треугольника не равна 180°. Вы обратили внимание на это обстоятельство и сделали из него вывод, который я считаю необычайно остроумным. Однако, поскольку кривизна пространства недоступна непосредственному наблюдению, ваш вывод оставался не более чем смелой гипотезой. Обычный флатландец, даже если он сведущ в науках, не поймет и, следовательно, отвергнет ваш выгод. Боюсь, что если бы вы попробовали поделиться своими удивительными умозаключениями с соотечественниками, то встретили бы лишь язвительные насмешки. Ваши «сожители» по пространству усомнились бы в ваших умственных способностях. Может быть, некоторые из них и выразили бы желание выслушать вас, но стоило бы вам уйти, как за вашей спиной начались бы разговоры о старческой немощи или оскудении ваших умственных способностей.

— И все же я считаю необходимым выступить в защиту истины, — собравшись с духом, заявил я. — Не только потому, что каждый, кому случалось сделать открытие, испытывает непреодолимую потребность возвестить об этом миру. В данном случае такое выступление необходимо для того, чтобы смыть с доктора Пункто пятно незаслуженных обвинений. Сначала его подозревали в том, что он преднамеренно произвел ошибочные измерения. Все наши попытки опровергнуть это нелепое мнение привели лишь к тому, что доктора Пункто просто стали считать плохим землемером, который с помощью небылиц пытается оправдать себя. Не пощадила молва и меня. Считали, что, поддерживая дружеские отношения с «погибшим человеком», я рискую своей репутацией и делаю это лишь из рыцарских побуждений, поскольку никаких более основательных причин для столь странной дружбы не существует.

Чтобы сделать нашу гипотезу более понятной, — продолжал я, — мы воспользуемся аналогией с Циркульландией. На этой модели хорошо видна искривленность одномерного пространства, незаметная для его обитателей. Тому, кто живет в одномерном искривленном мире, невозможно понять, что его пространство искривлено в некоем недоступном его восприятию направлении. Наконец, мы сошлемся па «свидетельские показания» нашего гостя из Трехмерия, наблюдавшего искривленность Флатландии.

Тут я умолк, ибо почувствовал, что несколько увлекся. Никогда не смогу я рассказать где-нибудь, а тем более на общем собрании членов физико-математического факультета, о своих встречах со Сферой. Меня примут за сумасшедшего или подумают, будто я общаюсь с потусторонним миром, что почти равносильно сношениям с самим дьяволом!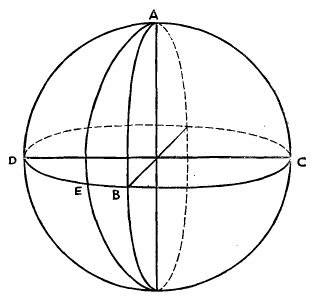

Сфера внимательно выслушала меня. Свое мнение она формулировала кратко. Прежде всего она просила нас не разглашать того, что нам известно. Знакомить ученых Флатландии со столь необычными теориями Сфера считала весьма опасным. Они не воспримут столь смелые теории и лишь обвинят нас с доктором Пункто в безумии.

Вскоре Сфера распрощалась и исчезла, предоставив нам самим решать наши проблемы.

После исчезновения Сферы мы сидели некоторое время молча. Каждый был занят своими мыслями. Но думали мы, по-видимому, об одном и том же, потому что вид у пас был одинаково мрачный. Причин для радости было мало: хотя теперь мы знали, что наши гипотезы имеют под собой прочную основу, рассчитывать на то, что нам удастся найти единомышленников, не приходилось. Мы твердо стояли на своем, были убеждены в своей правоте, по находились в полной изоляции, и это обстоятельство вряд ли могло служить утешением.

Первым правильность нашей точки зрения должен был бы признать физико-математический факультет, но ученые не разобрались, в чем истина, не приняли наших доводов. Убедят ли наши аргументы, даже подкрепленные сообщением Сферы, кого-нибудь другого? Чего мы достигнем, если попытаемся вопреки мнению факультета довести наши взгляды до всеобщего сведения? А если наши идеи получат у широкой публики более высокую оценку, чем у факультета? Нет, такое невозможно! Ведь против наших взглядов высказалось ученое общество, приговор которого принято считать беспристрастным. Какие бы аргументы мы ни приводили в подтверждение своей теории, к ним просто не будут прислушиваться.

Я решил спокойно все взвесить и не совершать необдуманных шагов.

— Должны же ученые мужи наконец понять, — сказал доктор Пункто, — что для объяснения необычных отклонений, обнаруженных при измерениях, необходимо выдвинуть какую-то гипотезу. Это единственно возможный подход. Нельзя же мириться с существованием необъяснимых явлений.

— Вполне согласен с вами, — ответил я, — но все не так просто, как кажется. Действительно, для объяснения странных явлений иногда приходится прибегать к странным гипотезам. Но если мы встанем на точку зрения ученых и взглянем на все со стороны, то так ли уж велика необходимость соглашаться с нашими весьма необычными выводами? Ведь до сих пор в правильность результатов измерений не верит никто, кроме нас. Невязки столь малы, что имеют доказательную силу лишь для того, кто достаточно долго занимался изучением результата измерения, и столь удивительны, что несведущему трудно устоять перед искушением и не приписать их ошибкам измерений.

— Сначала мы так и делали, — признался доктор Пункто, — по поскольку ошибки встречаются при любом измерении, то мы каждый раз настраивали свои приборы заново и в конце концов поняли, что невязки обусловлены не ошибками измерений.

— Правильно, — сказал я, — но попытайтесь заставить кого-нибудь затратить столько времени и энергии на нечто такое, что он считает совершенно бесполезным. Наука ищет объяснение твердо установленным фактам, но стремится достичь своей цели при помощи простейших гипотез. Разве не проще предположить, что двое каких-то чудаков заняли, мягко говоря, «необъективную позицию», чем соглашаться с гипотезами о структуре пространства, которые любому покажутся непонятными и странными? Нет, решительное неприятие подобных гипотез и есть та единственно научная (по крайней мере с точки зрения наших ученых мужей) позиция, которую могут занимать жрецы науки.

Доктор Пункто, мой собрат по науке и товарищ по несчастью, оценивал ситуацию так же, как и я. Мы поняли, что нам придется уступить. Моей жене, расчетливой, как все женщины, наша непосредственность была совершенно непонятна. Любая женщина, даже если она с сочувствием следит за тем, как ее муж преодолевает трудности и невзгоды, связанные с его умственной деятельностью, склонна рассматривать свойственное мужчинам стремление передать свои знания другим как своего рода навязчивую идею.

— Я бы на вашем месте бросила все это! — высказала свое мнение жена. — Пусть наукой занимаются другие, а не те, кому эти занятия не только не приносят никакой пользы, но доставляют одни лишь неприятности!

И хотя доктор Пункто и я расходились во мнениях с моей женой, все же мы не могли не признать, что в нашем положении благоразумнее всего последовать ее совету. Хотя бы на время!

— Если бы нашелся еще хоть кто-то, — мечтал доктор Пункто, — с научным складом ума, способный узреть истину, то нас по крайней мере было бы на одного больше.

— Ну, третьей является Сфера, — возразил я. — Но пока мы не можем просить ее объявиться открыто, ибо Нас тотчас же обвинят в колдовстве и в связи с дьяволом.

— Мне бы очень хотелось задать Сфере один вопрос, — вступил в разговор мой сын, до того молча слушавший нашу беседу. — Искривлен ли трехмерный мир в направлении, перпендикулярном трехмерному пространству и, следовательно, недоступном непосредственному восприятию трехмерных существ?

— Очень хорошо, что ты не спросил об этом Сферу, — ответил я. — Она достаточно умна для того, чтобы наблюдать за тем, что происходит в нашем пространстве и недоступно нашему восприятию. Но достает ли ей ума понять, изогнуто ли ее собственное пространство в направлении, недоступном ее восприятию, мне не известно. И я боюсь, что подобным вопросом мы могли бы поставить Сферу в неловкое положение.

— Я просто не успел спросить у Сферы, она исчезла так неожиданно, — честно признался мой сын, — но мне все равно хотелось бы узнать правильный ответ на свой вопрос.

— Возможно, тебе удастся сделать это позднее. Сейчас нам не следует настраивать Сферу против себя. Мы еще нуждаемся в ее помощи. Очень нуждаемся.

Наша беседа закончилась далеко за полночь, почти под утро. Доктор Пункто отправился к себе домой, а мы разошлись по комнатам и легли спать. Однако прошло немало времени, прежде чем мне удалось заснуть.

На следующее утро я вышел к своим домочадцам довольно поздно, и настроение у меня оставляло желать много лучшего. Зато мой внук был в превосходном расположении духа. Он играл в солдатики—фигурки, имевшие форму равнобедренных треугольников с очень острыми углами при вершине. Командиром отряда был равносторонний треугольник.

Внук выстроил одиннадцать солдатиков во главе с командиром по кругу, командир подал команду: «Шагом марш!», и все войско начало маршировать. Сначала сдвинулся с места сам командир, за ним первый солдатик, потом — второй и так далее.

Не знаю, что овладело мною — любопытство или желание отвлечься от нескончаемых мыслей о проблемах пространства, по только я спросил у внука, почему его солдатики начинают маршировать не одновременно. Задавая вопрос, я рассчитывал услышать в ответ:.

— Потому, что нельзя передвинуть всех солдатиков сразу.

Каково же было мое изумление, когда внук дал совершенно иной ответ:

— Потому, что солдатики слышат команду не одновременно.

Такой ответ поразил меня. Мальчик полагал, что звук распространяется от источника — командира — по цепочке, от одного солдатика к другому. Подобные физические представления у ребенка его возраста были явлением совершенно необычным, но разве мой внук не происходил из рода математиков и физиков?

Я был очень доволен и хотел, чтобы внук развил свою мысль подробнее. Поэтому я спросил:

— А разве звук распространяется по окружности, вдоль которой выстроены солдатики, а не по прямой — от командира к каждому солдатику?

Малыш озадаченно помолчал — над дедушкиным вопросом стоило задуматься, — по быстро нашелся:

— Нет, звук распространяется вдоль пути, по которому идут солдаты. Внутри окружности ничего нет.

Разумеется, последнюю «гипотезу» мой внук принял лишь потому, что ему так захотелось. Он стремился к тому, чтобы все вокруг было устроено просто. Солдатики выстроены вдоль окружности, маршируют они тоже вдоль окружности. Почему же звук должен распространяться вдоль различных прямых, идущих от командира к солдатикам и проходящим внутри окружности? С точки зрения моего внука, такое предположение было неоправданно сложным.

Затем мои мысли приняли повое направление. В солдатиках, выстроенных по кругу, я вдруг увидел модель Циркульландии с ее королем, окруженным своими подданными. Окружность, на которой обитал король, была его пространством. Звук королевского голоса распространялся вдоль окружности, то есть не по кратчайшему пути, ибо кратчайший путь проходит за пределами Циркульландии! Я снова вспомнил свой сон. Король Циркульландии, естественно, не мог понять меня, ибо не знал иного пространства, кроме своего собственного. И то, что он меня не понял, еще не свидетельствует о его глупости. Просто король не мог представить себе то, что лежит вне его пространства. Для него звук распространялся по кратчайшему пути, который возможен в Циркульландии. В школе нас учили, что кратчайший путь между двумя точками — это прямая, но на практике мы не всегда понимаем под кратчайшим путем прямую.

Неожиданно я вспомнил один эпизод, происшедший со мной в юности. Как-то раз я поздно вернулся домой, и отец устроил мне за это нагоняй. Он спросил, шел ли я домой кратчайшим путем. Разумеется, мой путь был далек от кратчайшего, но признаваться в этом мне не хотелось. Лгать я считал ниже своего достоинства и, пытаясь придумать какую-нибудь отговорку, схитрить, сказал отцу:

— Разумеется, я возвращался домой не кратчайшим путем, потому что идти кратчайшим путем просто невозможно.

— Почему, невозможно? — пожелал узнать мой отец.

— Потому, что кратчайший путь — это прямая, а она проходит через дома и другие препятствия.

Я уже неоднократно упоминал о том, что мы происходим из семьи, известной своими научными традициями, поэтому мой отец мог по достоинству оценить мое замечание.

Сейчас я снова задумался над тем, что же такое кратчайший путь. Предположим, что командир игрушечных солдатиков моего внука приказал своим подчиненным прибыть к нему кратчайшим путем. Как они должны поступить: идти к нему по дуге окружности или по прямой, соединяющей то место, где они находились в момент получения приказа, с тем местом, где находится командир, и проходящей внутри окружности?

Вполне может случиться, что командир только и следит за тем, как бы его подчиненные не нарушили строя и не сошли с окружности. Ему и в голову не придет, что солдат может приблизиться к нему по прямой. Не исключено также, что внутри окружности находится какое-то препятствие, например здание или запретная зона. В этом случае задача командира состоит в том, чтобы его подчиненные направлялись к нему не по пути, кратчайшему с точки зрения геометрии, а по практически наиболее короткому пути, то есть шли вдоль дуги окружности.

Аналогично обстоит дело и в Циркульландии. Король ничего не знает о «территории» внутри окружности. Для него не существует другой возможности, кроме как двигаться в своем собственном пространстве. О том, что возможен более короткий путь, пролегающий за пределами его пространства, король просто не знает. Может быть, до этого мог бы додуматься какой-нибудь особенно проницательный и хитроумный математик из Циркульландии, однако такому гению не удалось бы убедить «собратьев по пространству» в правильности своих выводов. Все, что принадлежит пространству, не может покинуть пределы пространства. Звук также не может выйти за пределы пространства. Следовательно, распространяясь в пространстве, звук должен как бы следовать за кривизной пространства. Странно, очень странно!

Я устал и почувствовал, что больше не в силах размышлять о кратчайших путях и тому подобных вопросах. Незаметно я уснул. Удивительно, но на этот раз мне приснилась не Лайнландия, и я, многомудрый флатландец, не спускался в одномерное пространство, чтобы просветить его обитателей и открыть им истину, известную мне до мельчайших подробностей, поскольку я своим глазом мог созерцать истинное положение вещей, недоступное непосредственному восприятию лайнландца. Нет, мне приснился совсем другой сон. Мне почудилось, будто я — Сфера, гиперокружность из трехмерного пространства, и наношу визит в свой собственный мир, в свою собственную Флатландию. Нет, не Флатландию, а Сферландию, ибо я отчетливо видел, что мир искривлен в направлении, ныне доступном моему созерцанию, направлении, которое ранее мне никогда не доводилось видеть. Теперь я мог рассматривать его сколько угодно, ибо я был Сферой, мудрой Сферой! Ничто в нашем двумерном пространстве не осталось сокрытым от меня. Впрочем, я постиг все без особого труда, ибо был теперь трехмерным существом.

А вот и мой дом! Я смотрел на него сверху, извне нашего пространства, откуда мне никогда не приходилось видеть его. Вон там моя жена. Дети! Внуки! Поистине поразительное зрелище! А вот и я сам, жалкий двумерный шестиугольник. Я всегда считал себя важной, представительной фигурой, но как убого я выгляжу в действительности, плоское двумерное существо.

Интересно, могу ли я приблизиться к самому себе? Могу ли я рассказать самому себе, как выглядит все, если взглянуть на наше пространство извне? Нет! Я бы ни за что не поверил, ибо слишком глуп! Нет, не глуп, а ограничен, ибо способен воспринимать лишь двумерные картины всего, что окружает меня.

Нет, не буду тревожить старого ученого! Ему и так хватает сложных проблем! Пусть спит спокойно! Лучше я рассмотрю как следует двумерный мир, мой собственный мир, мою искривленную Флатландию. Хотелось бы знать, смогу ли я, проснувшись у себя дома, там, внизу, припомнить вес, что мне довелось увидеть? Удивительно! Я вижу иод собой весь город с его домами, улицами, деревьями. Отчетливо различаю движение на улицах. Вижу все рядом, совсем близко. Интересно, как такое может происходить во сне? Ведь мне хороню известно, что я сплю. Какой прекрасный сон! И какой странный!

Я посмотрел направо, потом налево, огляделся по сторонам. Мир, мой мир, простирался подо мной во все стороны, уходя в бесконечность. Впрочем, ведь это невозможно: наш мир не бесконечен. Он не простирается во все стороны неограниченно далеко. Наш мир изогнут, искривлен. Я могу обойти вокруг него, облететь вокруг моего мира, моей сферической Флатландии. Странно! С какой легкостью я представляю себе все это. Просто удивительно! Может быть, меня во сне вдохновила Сфера? Может быть, я смотрю на все глазами своего друга Сферы? Вполне возможно. Что сказать по этому поводу?

Да, у Сферы есть явное преимущество перед нами: она все видит. Хотя особого искусства для этого не требуется. То, что видит Сфера, я постигаю своим разумом, я, флатландец, хотя меня, живущего в сферической Флатландии, правильнее было бы называть сферландцем. Сфере не нужно напрягать свой разум или строить гипотезы: ей достаточно взглянуть на все со своей трехмерной точки зрения.

Интересно, как распространяется свет? Прямо? Вдоль прямых? Нет, конечно же, нет! Лучи света не могут выходить за пределы пространства, своего пространства. Значит, лучи света должны искривляться вслед за пространством, ибо они лежат в этом пространстве! Нам, обитателям Сферландии, лучи света кажутся прямолинейными. Мы полагаем, будто свет распространяется вдоль прямых. Лучи света действительно не искривлены относительно нашего пространства, а изгибаются вслед за ним. Они просто обязаны вести себя так. Но если взглянуть на Сферландию извне, то лучи света перестанут казаться прямыми, ибо в действительности они распространяются вдоль кратчайших из всех линии, какие только можно провести в нашем пространстве! То же самое можно сказать и о линиях, вдоль которых в Сферландии распространяется звук. Они также не являются прямыми. Но тогда… Хотя Сфера и уступает мне по уму, она все же должна понять, что ее пространство искривлено. Да, да! Ее трехмерное пространство искривлено в некоем невидимом для нее направлении, и лучи света в трехмерном пространстве также отличны от прямых. Свет в трехмерном пространстве распространяется вдоль кратчайших из линий, которые можно провести в этом пространстве. Лучи света должны быть изогнуты в невидимом для обитателей Трехмерия направлении так же, как изогнуто само трехмерное пространство.

— Сфера не может этого не понять. Если она все же не поймет, что ее пространство искривлено, то, значит, я гораздо умнее ее.

Последние слова я произнес громогласно. Я и сам услышал, но было поздно. Неожиданно до меня донесся голос, голос Сферы, с упреком произнесший:

— И ты, плоское двумерное существо, еще осмеливаешься думать, будто ты в чем-то превосходишь меня! Я трехмерна и смотрю на ваш мир сверху вниз. Неблагодарный хвастун! Отправляйся назад, в свой мирок! Одного взгляда на него было достаточно, чтобы я сразу все поняла. А ты еще осмеливаешься ругать меня и принимать за глупца, неспособного понять, что его мир искривлен! Нет, я не вижу кривизны своего мира но той простой причине, что ее не существует. Мой мир плоский. Плоский, понимаешь ли ты это? Ты живешь в искривленном мире, а не я. А теперь довольно, отправляйся к себе назад!

Я проснулся у себя в комнате. Что это было: сон или Сфера действительно вознесла меня в трехмерное пространство? Позволила ли она мне бросить взгляд на мой искривленный мир? Как мне ответить на этот вопрос? Если все это мне не приснилось, то просто ужасно! Я оскорбил Сферу, моего доброго друга и наставника, и она никогда больше не прибудет к нам с визитом под Новый год! Столь же решительно, как в свое время она порвала отношения с моим дедом, Сфера перестанет общаться со мной. Об этом лучше не думать!