Постоянные календари. Вследствие упомянутых недостатков григорианского календаря определение дня недели календарных дат очень затруднено, а такие определения необходимы не только при изучении истории или определении знаменательных дат, но и при археологических и литературных исследованиях и в других самых различных случаях. Например, при расчетах заработной платы, при определении числа рабочих дней в году, средней производительности Труда, при планировании пятилетних планов и других мероприятий, при определении объема продукции за некоторый отрезок времени, а также при возникновении необходимости установить день недели прошедших или предстоящих дат. Они необходимы в судебной практике и установлении дат различных мероприятий, проводимых один раз в несколько лет, например олимпиад.

Все это и явилось причиной дальнейшего развития календарных систем путем разработки постоянных («вечных») календарей, позволяющих решение перечисленных выше задач производить с меньшей затратой времени и труда.

В настоящее время известны постоянные календари самых различных устройств, составленные как на короткие, так и на длительные промежутки времени, позволяющие определять день недели любой календарной даты юлианского или григорианского календаря или сразу обоих, — универсальные календари. Все многообразие постоянных календарей можно разделить на календари аналитические — формулы различной сложности, позволяющие по заданной дате вычислять день нежели любой прошедшей и будущей календарной даты, и табличные — таблицы различной конструкции как с неподвижными, так и с подвижными частями.

Постоянные табличные календари могут быть краткосрочными (однопериодными), предназначенными лишь для одного 28-летнего периода (цикла) [51]; среднесрочными (вековыми), предназначенными лишь для одного определенного периода в пределах от 28 до 100 лет; долгосрочными (постоянными), рассчитанными на значительные по продолжительности периоды от 100 и более лет.

В последние сто лет в разных странах предложены различные календарные формулы [52]; из них первая была опубликована в России Н. И. Черухиным — (Русская старина. — 1873. — № 7). Первое же правило, позволяющее определять по заданной дате день недели, было опубликовано В. И. Штейнгелем в 1819 г. в его работе «Опыт времяисчисления» (СПб, 1819).

Поскольку все существующие календарные формулы опубликованы без их вывода, можно считать, что они были получены методом подбора. Этим и объясняется большая их разновидность. При этом многие формулы действительны только для нового стиля и не позволяют непосредственно определять день недели календарных событий, имевших место в нашей стране до 1918 г. Формулы отличаются еще и тем, что в одних за первый день недели принято воскресенье, а в других — понедельник. (Только с 1976 г. согласно стандарту Международной организации стандартов 2015–1976 за первый день недели принят понедельник.)

Большинство формул из-за своей сложности трудно запоминаются. Для некоторых требуется подсчитывать количество дней, прошедших от начала года до заданной даты, а для других — для каждого месяца определять свой коэффициент.

При выводе формулы примем следующие обозначения: К — календарное число месяца; М — коэффициент месяца; J — полный номер года н. э.; Д — порядковый номер года в столетии; Г' — сдвиг дней недели по годам; Г — коэффициент года; В — коэффициент века; С — число полных прошедших столетий; [] — целая часть частного от деления (неполное частное); | | — остаток от деления, причем если делимое меньше делителя, остаток равен делимому; d — порядковый номер дня недели (0 — воскресенье, вс; 1 — понедельник, пн; 2 — вторник, вт; 3 — среда, ср; 4 — четверг, чт; 5 — пятница, пт; 6 — суббота, сб).

День недели календарной даты определяется как остаток от деления суммы чисел К, М, Г и В на 7:

d = |(K+ M + Г+В) / 7 | (1)

Сделаем предположение, что 1 января 1 г. п. э. был понедельник (= 1). Тогда для дат января первого года день недели будет определяться по формуле

d = |К / 7 |.

Так как в январе 31 день, то день недели в феврале первого года определится по формуле

d = |(К + (31–28)) / 7 | = |(K + 3) / 7 |.

Здесь 28 — ближайшее к 31 число, кратное семи, которое мы вычитаем для упрощения вычислений.

Так как в феврале первого года 28 дней, то день недели в марте определяется так же, как и в феврале. В марте 31 день, поэтому для апреля получим формулу

d = |(К + 3 + (31–28)) / 7 | = |(K + 6) / 7 |.

Аналогично получим формулы для остальных месяцев. В этих формулах числа, прибавляемые к календарному числу К, суть коэффициенты месяцев М, которые мы свели в табл. 9.

Таким образом, день недели для первого года н. э. будет определяться по формуле

d = |(K + M) / 7 |. (2)

Объединив повторяющиеся в табл. 9 значения М для разных месяцев, получим табл. 10.

Так как в простом году 52 недели и один день (365 = 52×7 + 1), то для второго года н. э. календарная формула примет вид

d = |(K + M + 1) / 7 |.

а для третьего

d = |(К + М + 2) / 7 |.

Следующий год (четвертый) — високосный; в нем 366 дней (за счет увеличения числа дней в феврале: 29 вместо 28). Поэтому для 4 г. н. э. календарная формула принимает вид для января и февраля

d = |(K = M + 3) / 7 |.

а для месяцев с марта по декабрь

d = |(K = M + 4) / 7 |.

В табл. 11 приведены коэффициенты М для високосных (вис.) и невисокосных — простых (пр.) лет. Так как сдвиг дней недели по годам Г' в четырехлетиях 1–4, 5–8, 9–12 и т. д. происходит одинаково, составим таблиц значений Г' для J от 1 до 60 лет (табл. 12). Мы видим, что в каждом следующем четырехлетии значение сдвига Г' «увеличивается» на 5. Это позволяет выразить его для високосных годов (J_вис) в виде формулы

Г' = |(5(Jвис:4) — 1) / 7)|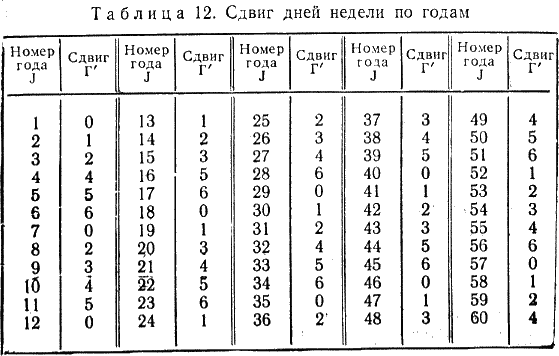

а для простых (J_np) в виде формулы

Г' = |(5 (J_вис: 4) — 1 + (J_пр — J_вис)) / 7 |,

где J_вс — ближайший меньший високосный год [53], а так как

J_вис: 4 = [J_пр: 4],

(3)

то общей формулой для Г' для простых и високосных годов будет

Г' =|(J + [J: 4] — 1) / 7 |. (3)

Упростим формулу (3), убрав в ней «—1». Чтобы сумма М + Г в формуле (1) осталась неизменной, уменьшим на единицу значения коэффициентов М в табл. 11 (при этом 0 считается равным 7). Новые значения коэффициентов М приведены в табл. 13, а формула (3) примет вид

Г' = |(J + [J: 4]) / 7 |.

(4)

В формуле (4) полный порядковый номер года J, выражающийся для нашего времени четырехзначными числами, усложняет вычисления. Если обозначить число тысяч буквой а, число сотен — буквой Ь, число десятков — буквой с и число единиц — буквой f, то номер года J можно записать в виде

J= 1000а + 100b + 10с + f

и тогда

[J: 4] = 250а + 25b + [(10с + f): 4],

а

J + [J: 4] = 100a + 100b + 10c + f + 250a + 25b + [(10c + f): 4] = 1250а+ 125b + 10c + f + [(10c + f): 4].

Так как

|(1250a + 125b) / 7 | = |(7×170a + 60a + 7×17b + 6b) / 7 | = |6(10a + b) / 7 |.

то

(J + [J: 4]) / 7 = 10c + f + |(10с + f): 4 | + 6 (10а + Ь) / 7.

Если же учесть, что 10а + b = С — это число полных прошедших столетий (например, для 1986 г. С = 19 = 10×1 + 9), а 10с + f = Д — порядковый номер года в столетии, то формула (4) примет вид

Г' = |(Д + [Д: 4]) / 7 | + |6c / 7 |. (5)

Значения второго слагаемого с течением веков циклически повторяются (см. табл. 14); это коэффициент века В. Первое же слагаемое будет коэффициентом года Г,

Г' = |(Д + [Д: 4]) / 7 |. (6)

Следует учитывать, что порядковый номер Д года J в столетии имеет значения от 1 до 100, и поэтому для всех вековых лет, например 1800, 1900, 2000 гг. и т. д., Д = 100. Для I в. (годы 1–100) число полных прошедших столетий С = 0, для II в. (годы 101–200) С = 1 и т. д.

В табл. 14 приведены значения коэффициента века В (по старому стилю) для н. э.; из нее следует, что повторяемость юлианского. календаря происходит через 700 лет.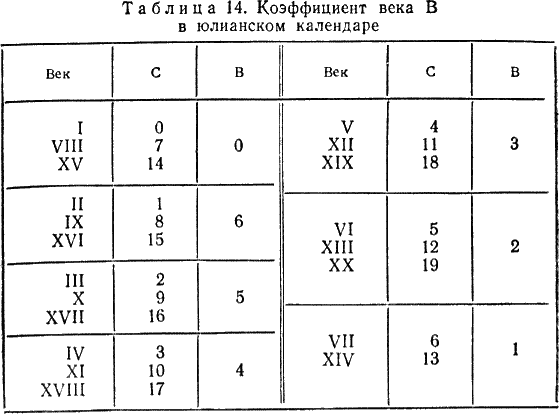

В начале изложения мы условно приняли, что первый день нашей эры (1 января 1 года первого века) был понедельником. Установим теперь значения коэффициентов М, которые дадут возможность правильно определять дни недели. Для этого используем точную дату какого-либо известного события.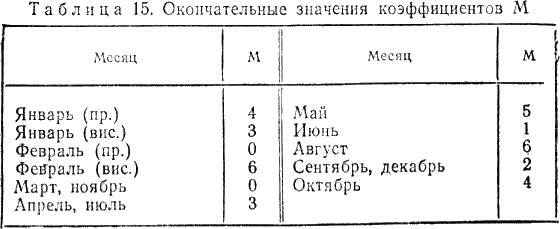

Например, что 9 января 1905 г. было воскресенье («Кровавое воскресенье»). Для этой даты d = 0, К = 9, Г = |(5 + [5: 4]) / 7 | = 6, а В = 2. Подставляя эти данные в формулу (1), получим 0 = | (9 = M + 6 + 2) / 7 |, откуда М = — |17 / 7 | = —3. (Если для коэффициента М получается отрицательное значение, то его следует заменить положительным, прибавляя ближайшее большее число, кратное 7. В нашем случае —3 + 7 = 4.) Коэффициенты остальных месяцев можно установить исходя из сравнения с табл. 13. Вообще же их можно вычислить, взяв табель-календарь любого года. Окончательные значения М приведены в табл. 15. Теперь можно определить, каким днем недели было 1 января 1 г. н. э. Для этой легендарной даты К = 1, М = 4, Г = |(1 + [1: 4] / 7 | = 1 и В = 0, следовательно, d = |(1+ 4 + 1 + 0) / 7 | = 6 — суббота.

В новом стиле все вековые годы, кроме тех, число столетий в номере которых делится на 4 (например, 1600, 2000, 24 000 гг. и т. д.), невисокосные. Поэтому коэффициенты века В для этих годов будут другими.

Для определения значений поправок к коэффициенту века В для нового стиля следует учитывать, что при реформе юлианского календаря было принято следующую после четверга 4 октября 1582 г. дату считать пятницей 15 октября.

При этих условиях для 15 октября 1582 г. (С = 15) получаем d = 5, К =15, М = 4 и Г = |(82 + [82: 4]) / 7 | = 4.

Подставляя эти значения в формулу (1), получим 5 = |(15 + 4 + 4 +В) / 7 |, откуда В = |–18/7 | = |–14/7 | = 3.

Для юлианского календаря коэффициент века B = |(6C + P) / 7 |, а для григорианского к нему надо найти поправку Р, определяемую из соотношения

B = |(6c +P) / 7 |.

Так как в этих вычислениях применяется правило остатков, то формула преобразуется к виду

P = |(B + 6С) / 7 |.

В табл. 16 приведены эти поправки Р и коэффициенты века В для нового стиля с XVI по XXIII вв. Как видно из таблицы, коэффициенты В имеют всего четыре значения 3, 2, 0 и 5, которые циклически повторяются через 400 лет.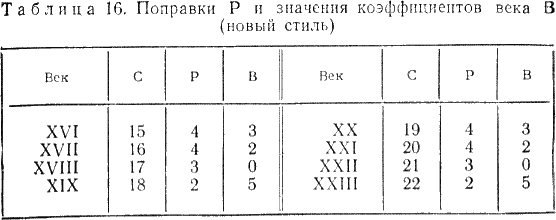

С введением григорианского календаря появились особые простые вековые годы 1700, 1800, 1900; для которых коэффициент года Г, определяемый по формуле (6), необходимо уменьшать на единицу, т. е. для этих лет

Г = |(100+ [100:4])/7 | = 5. (7)

Что касается вековых лет, число сотен которых кратно четырем, например, 1600, 2000 и т. д., то для нового стиля они остаются високосными, и коэффициент года для них определяется по общему правилу:

Г = |(100 + [100:4]/7 | = 6.

Итак, порядковый номер d дня недели любой календарной даты задается формулой (1) (см. с. 102). Значение коэффициента месяца М берется из табл. 15, коэффициент года Г вычисляется по формуле (6) или (7), а значение коэффициента века В берется для старого стиля из табл. 14, а для нового из табл. 16. Напомним еще раз, что если сумма К + М + Г + В меньше семи, то остаток от деления на семь равен самой сумме. То же правило действует при делении на четыре.

Начиная с 1873 года календарные формулы публиковались в разных странах. Входящие в них элементы имели различные обозначения и порядок расположения. Для возможности исследования формул мы свели их в таблицу (табл. 17) в хронологическом порядке с одинаковыми условными обозначениями (см. § 23) и расположением элементов К, М, Г и В.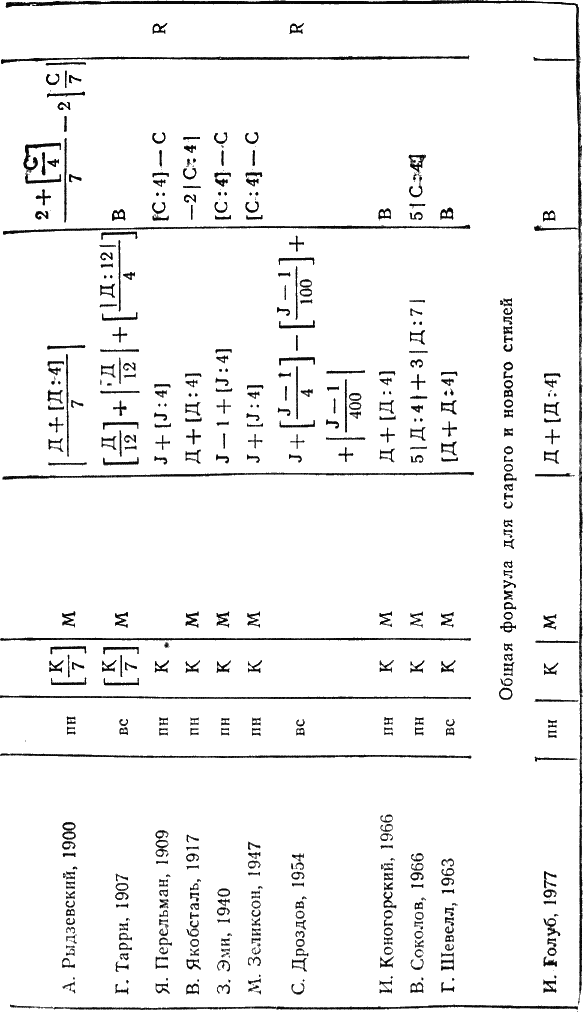

В большинстве формул коэффициент месяца М дается в виде таблицы с готовыми значениями — числами от 0 до 6. В некоторых формулах (Перевощиков, Дроздов и Перельман) вместо готовых значений коэффициента месяца М используется число дней от начала года R. Это усложняет вычисления. Также усложняет вычисления примененное Целлером и Каменьщиковым определение коэффициента месяца М в зависимости от порядкового номера месяца в году m (при этом январь и февраль високосного года считаются 13-м и 14-м месяцами предыдущего года). Формулы отличаются еще и тем, что при вычислении коэффициента года в одних вводится полный номер года J, а в других его порядковый номер в столетий Д, что упрощает вычисления.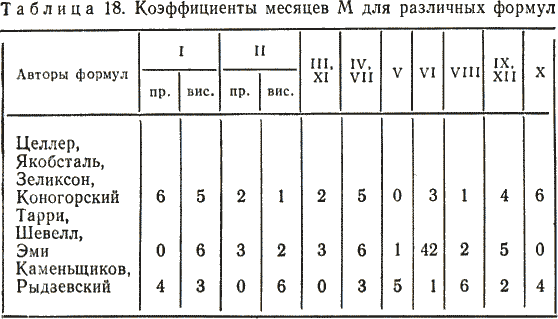

В табл. 18 приведены значения коэффициента месяца М для формул, представленных в табл. 17. Проверка показала, что все формулы дают правильные ответы для всех дат за исключением простых (невисокосных) вековых лет по новому стилю, — т. е. годов 1700, 1800, 1900, 2100, 2200, 2300 и т. д. Для этих годов необходимо уменьшать на единицу коэффициент года Г (см. формулу (7)).

Определение дня недели значительно упрощается с помощью постоянных табель-календарей. Если подсчитать для каждого года и месяца заданного столетия величины Е, представляющие остатки от деления на 7 (т. е. числа от 0 до 6) суммы коэффициентов месяца М, года Г и века В,

Е = |(M + Г + B)/7 |,

и свести их в таблицу, то определение дня недели выразится формулой

d = |(К + Е)/7 |,

где К — календарное число месяца.

Каждый замечал, что распределение дней недели по числам года повторяется. Эта повторяемость имеет определенную закономерность. Так, если номер года в столетии при делении на 4 дает в остатке 1 (год, следующий за високосным), то следующий год с тем же распределением дней недели повторится через 6 лет, если же остаток 2 или 3, то следующий такой же год будет через 11 лет. Так, для 1985 г. (85 = 21 × 4 + 1) это будет год 1991, а для годов 1986 и 1987 (соответственно 21 × 4 + 2 и 21 × 4 + 3) — годы 1997 и 1998. Високосные годы с одинаковым распределением дней педели повторяются только через 28 лет. В юлианском календаре ровно через 100 лет даты отступают по дням недели на одну позицию назад, и полная повторяемость дней педели происходит через 700 лет. В григорианском календаре столетия начинаются только с воскресенья, субботы, четверга и вторника, и здесь полный цикл завершается по прошествии 400 лет.

В книге А. В. Буткевича и М. С. Зеликсона (см. список литературы) представлена обширная коллекция из 60 постоянных табель-календарей без их математического обоснования и подробного анализа. Рассмотрим их отличия. Часть из них рассчитана на старый стиль (юлианский календарь), а часть на новый стиль (григорианский календарь). Следует отметить, что табель-календарь на XX в. по новому стилю совпадает с календарем для XIX в. по старому стилю.

Другое отличие состоит в том, что в одних календарях для определения порядкового номера дня недели приходится находить остатки от деления на 7 суммы К + Е, а в других день недели определяется по таблице готовых значений этой суммы. Сумма К + Е имеет значения от 1 до 37, при этом значениям 1, 8, 15, 22, 29 и 36 соответствует один день недели, значениям 2, 9, 16, 23, 30, 37 — следующий и т. д. Такая таблица дается в ряде вечных календарей.

Еще одно отличие заключается в том, что в одних календарях приводятся 12 столбцов значений Е, а а других 7. Это следует из таблиц 11, 13, 15, в которых можно объединить также январь простого года и октябрь, январь високосного года и апрель, июль и т. д.

Остается определить, па какие сроки целесообразно издавать постоянные табель-календари. В книге А. В. Буткевича и М. С. Зеликсона такие календари подразделяются на краткосрочные со сроком действия от одного до 25 лет, среднесрочные (от 34 до 200 лет) и долгосрочные (200–3000 лет). По нашему мнению, наименьший срок, на который нужно рассчитывать постоянные табель-календари, — это столетие. Предлагаем постоянный табель-календарь на XX в. по новому стилю (табл. 19), состоящий из частей А и Б. Он пригоден также для XIX в. по старому стилю. Если к нему добавить таблицу поправок (табл. 20), то он будет пригоден для 1–2000 гг. по старому стилю и для 1501–2301 гг. по новому стилю. Для определения дня недели нужно взять значение Е на пересечении номера года в столетии с колонкой месяца для високосного или невисокосного года в части А и прибавить к нему число месяца К. По полученной сумме в части Б найдем день недели.

Пример 1. Определить, в какой день недели было 9 мая 1945 г. В части А слева находим число 45. Справа против него в колонке «май» находим число 1, которое прибавляем к календарному числу: 9 + 1 = 10. Эту сумму находим во втором слева вертикальном столбце части Б, и против нее в последнем крайнем столбце читаем «ср», т. е. «среда».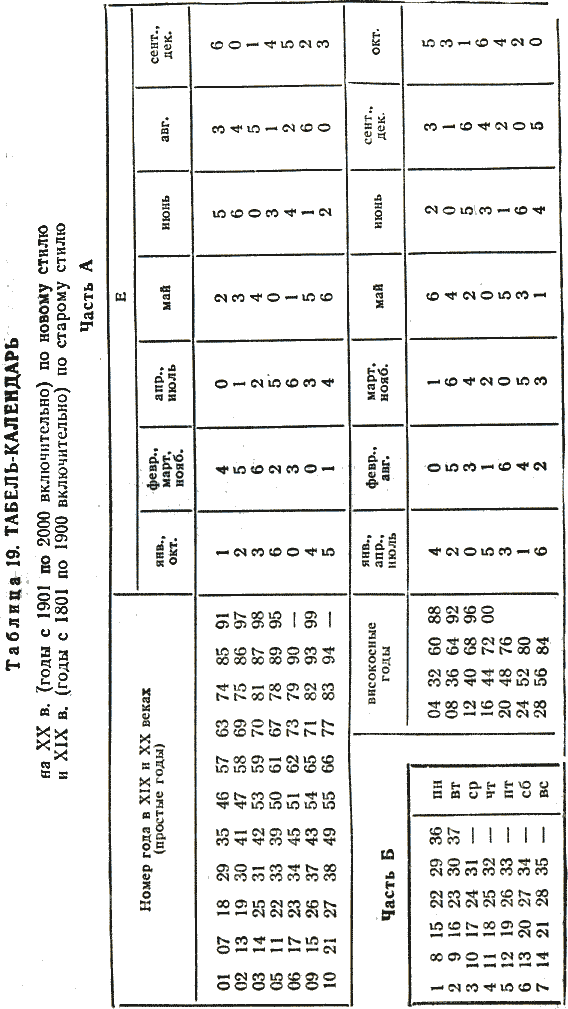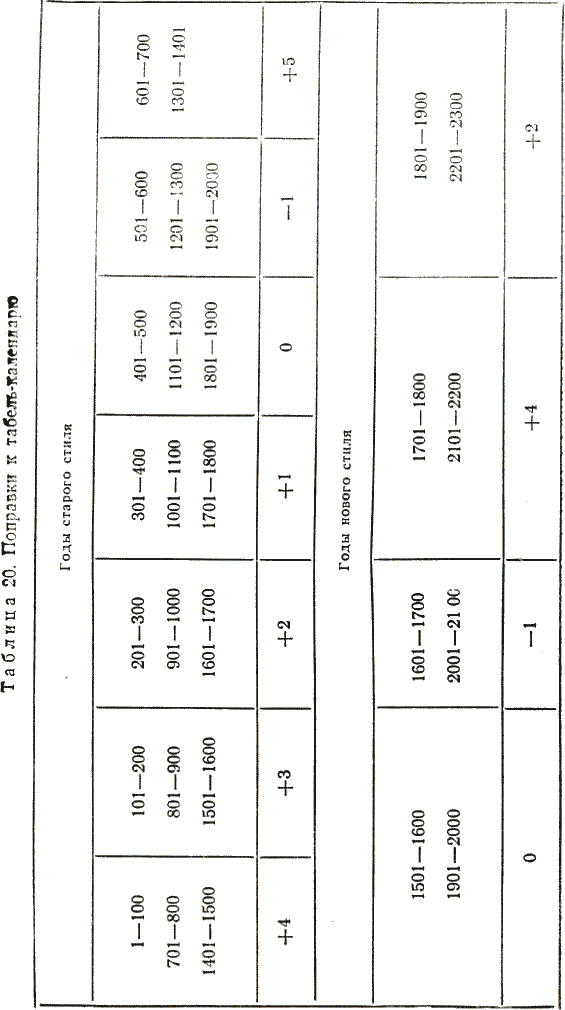

Пример 2. Определить, в какой день недели было 9 января 1905 г. (старый стиль). По аналогии с первым примером слева в части А находим 05 (левый крайний столбец) и против него в колонке «янв.» читаем «6», а так как это событие задано календарной датой старого стиля, вычитаем единицу, т. е. 9 + 6–1 = 14. Эту сумму (14) находим в части Б (второй слева столбец) и против 14 в правом крайнем столбце находим ответ «вс», т. е. воскресенье («Кровавое воскресенье»).

Пример 3. Определить, в какой день недели будет 7 ноября в 2017 г. — столетие Великой Октябрьской социалистической революции. Найдя в части А число 17 (две последние цифры номера заданного года), против него в вертикальном столбце «нояб.» читаем цифру 3.2017 г. относится к XXI в., поэтому вычитаем единицу. Получим 7 + 3–1 = 9, и против этого числа в части Б (вторая колонка) в правом крайнем столбце читаем «вт». Следовательно, 100-летие Великого Октября будет во вторник.

Пример 4. Определить, какой будет день недели 1 мая 2000 г., являющегося високосным. В части А находим две последние цифры века-в данном случае «00», и против них в колонке «май» читаем «0». Следовательно, 1 + 0 = 1. В первой строке части Б находим «пн», т. е. понедельник.

Примечания:

5

Ленин В. И. Полн. собр. соч. —Т. 18. — С. 181.

51

Такой период выбран не случайно: число 28 является общим наименьшим кратным двух чисел — 4 (через четыре года повторяется високосный год) и 7 (число дней в неделе). В настоящее время в нашей стране выпускаются календари на более короткие промежутки времени — например, с 1976 по 2000 гг.

52

См. Буткевич А. В., Зеликсон М. С. Вечные календари. — 2-е изд., перераб. и доп. — М.: Наука, 1984.

53

Для 1, 2, 3 годов н. э. таким ближайшим високосным годом является «нулевой» год.