40. ПРОБЛЕМА РЕАЛЬНОСТИ В КВАНТОВОЙ ФИЗИКЕ

Классическая механика в микромире и для околосвет-ных скоростей неприменима. Релятивистская физика, основанная на теории относительности, применима к скоростям, близким к скорости света, а квантовая – к миру атомов и элементарных частиц.

Рассмотрим релятивистскую формулу массы: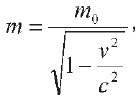

где m 0 – масса покоя тела, v – скорость его движения. При уменьшении отношения до нуля, что может быть достигнуто или при v = 0 (покой), или при c = БЕСКОНЕЧНОСТИ(идея мгновенного распространения света), масса становится величиной постоянной m = m0, как это и признавалось в классической механике до А. Эйнштейна.

Известное соотношение E=m ? c2дает для массы то же переменное значение: m = E/c2

Скорость света есть величина постоянная, но сообщаемая телу извне энергия должна сказываться на величине массы. Релятивистская формула сложения скоростей в случае движения со скоростью света (фотон, нейтрино) приводит к выводу: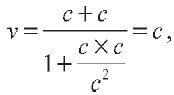

т. е. два фотона, обладающих каждый скоростью с, при движении навстречу друг другу сближаются не со скоростью с2как этого требовал бы здравый смысл, а все с той же скоростью с.

Если в релятивистской физике границы применимости были связаны с огромностью и постоянством скорости света (с = 300 000 км/с), то в квантовой механике границы применения классической физики связаны с малостью постоянной Планка (h= 6,62 ? 1 0-27эрг ? с).

Волновые свойства материи, которые не рассматривает классическая физика, характеризуются длиной волны де Бройля: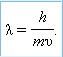

Чем короче длина волны, тем больше импульс – основная характеристика материальной частицы, и, наоборот, увеличение импульса (или скорости) приводит к уменьшению длины волны, т. е. уменьшению волновых свойств. Для микромира с его частицами малой массы длина волны достигает размеров, позволяющих измерить ее и обнаружить волновую природу частиц (явление дифракции). В макромире вследствие чрезвычайной малости hдлина волны получается исчезающе-малой.

Так, если человек средней массы идет со скоростью 5 км/ч, то длина соответствующей волны получается порядка 10-23см.

Математически соотношение неопределенности можно записать так:

?р?х = h где ?р и ?х – неточности (неопределенности) в значении импульса и координаты, а h=h/2? Записав ?р = mAv можно придать соотношению неопределенности иную форму:

?v?x = x/m

Если импульс частицы известен точно, то ?х = x/Q т.е. координаты совершенно неопределенны. В классической механике, где импульс и координаты вполне определены, соотношение выглядит так: ?р?х = 0. Чем ближе мы к этому предельному случаю, тем с большим правом можно применять законы классической механики. Для дробинки массой в 1 г такая неточность в макромире неощутима.